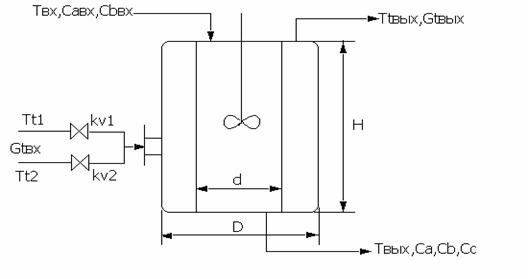
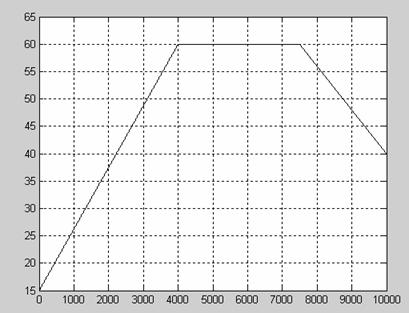
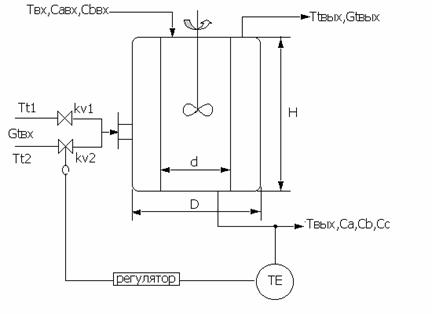
Курсовая: Моделирование систем управления

Курсовая: Моделирование систем управления

СОДЕРЖАНИЕ

1 Задание............................

2 Анализ технологического аппарата как объекта управления......

3 Математическое описание динамики объекта управления.......

4 Исследование динамики объекта управления.............

5 Исследование переходных процессов в АСР............

Заключение.........................

Список используемых источников................

Перечень приложений......................

1 ЗАДАНИЕ

Химический реактор периодического действия с мешалкой и рубашкой.

В снабженный мешалкой химический реактор (рис.1) с постоянным объемом

реакционной смеси, внутренним диаметром 1 м, внешним диаметром 1.1 м и высотой

1.515 м, загружается жидкая смесь веществ А и В температурой tвх=15ºС,

концентраций CАвх=20 моль/м3 и CВвх

=100 моль/м3. В ре­акторе протекает химическая реакция по схеме А + В

С со скоростью реакции r=A*exp(-E/(R*T)*СA*CB,моль/(м

3*с). Здесь множитель А = 30 (моль*с*м3)-1, энергия

активации Е = 40000 Дж/моль, универсальная газо­вая постоянная R=8.314

Дж/(моль*К) и температура смеси в реак­торе Т, К. Тепловой эффект

экзотермической химической реакции

10000 Дж/моль. Для поддержания необходимых условий протекания реакции в рубашку

для нагрева подается теплоноситель температурой tтгвх=90

0С, для охлаждения tтхвх=150С.

Коэффициент теплопередачи от теплоносителя к реакционной массе Кт =

1000 Дж/(м2*с*К). На входе в рубашку установлены клапаны для подачи

горячего и холодного теплоносителя с про­пускной способностью Kv

1 и Kv2 соответственно. Давление

теплоносителя перед клапаном равно Рт = 230000 Па.

Давление теплоносителя в рубашке равно Ра= 101325 Па. Теплоем­кости

и плотности реакционной массы и теплоносителя считаются постоянными и равны

соответственно 3500 Дж/(кг*К), 800 кг/м3; Срт= 4100

Дж/(кг*К), р2= 1000 кг/м3.

Параметры системы регулирования: Пи - регулятор, зона нечувствительности

D=0%, инерционность датчика Т=170 с, диапазон измерения - 50 –(+ 120

0С.)

Требуется: 1) произвести моделирование СУ, которое включает в себя

математическое описание технологического аппарата как ОУ, регулятора,

исполнительного механизма и чувствительного элемента; 2) для объекта химический

реактор периодического действия с мешалкой и рубашкой (рис.1) получить и

проанализировать: а) динамические характеристики вида СА(t), СВ

(t),

Сc(t), Тт(t), Т(t) ; б) переходные характеристики по

каналам Твых (t),Твых изм (t)

при задающем воздействии Твх (рис.2) ; в) переходные характеристики по

каналам передачи воздействия tтгвх

Твых tтхвх

Твых при соответствующем изменении значений пропускной способности

клапанов на входе в рубашку и настроек регулятора.

Рис.1 Химический реактор с рубашкой и мешалкой

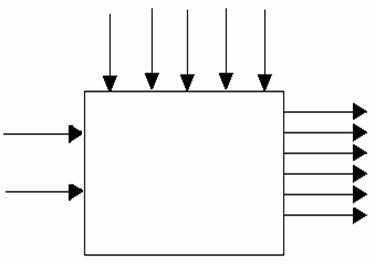
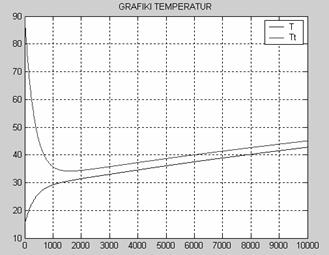
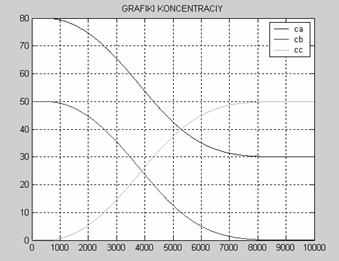
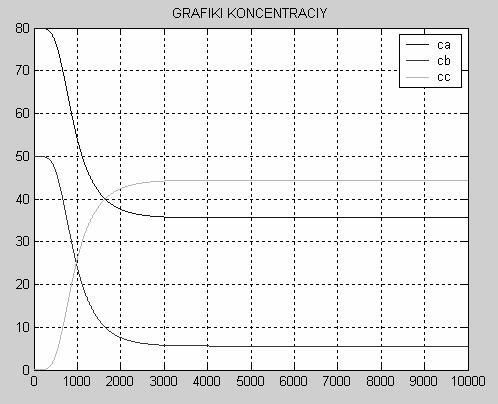
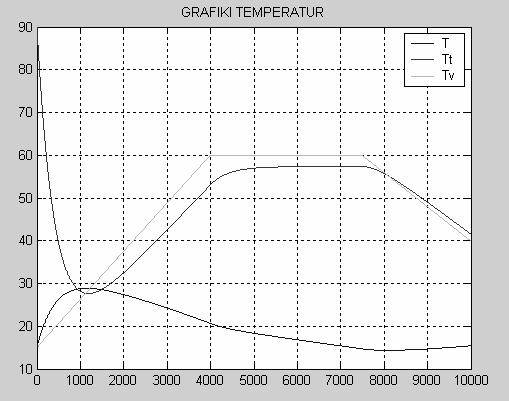
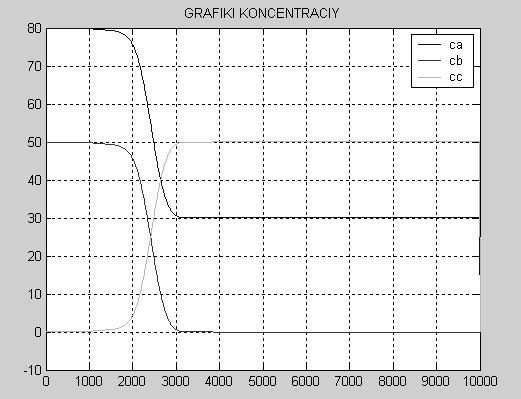
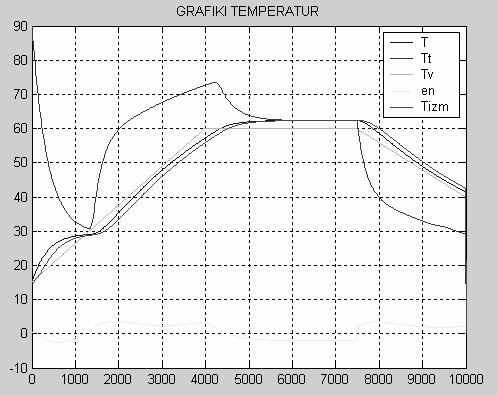
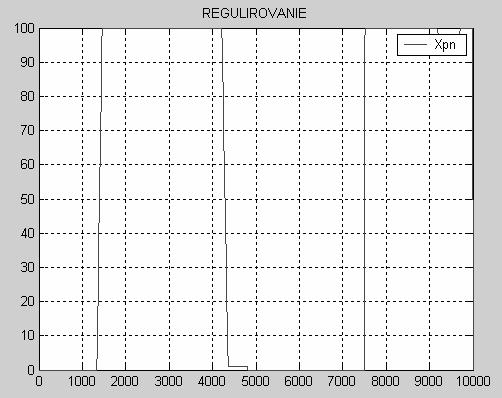
Рис. 2 Задающее воздействие

2 АНАЛИЗ ТЕХНОЛОГИЧЕСКОГО

АППАРАТА КАК ОБЪЕКТА

УПРАВЛЕНИЯ

Рассмотрим химический реактор с мешалкой и рубашкой как объект управления.

Любой технологический процесс как объект управления характеризуется

следующими основными группами переменных.

1. Переменные, изменением которых система регулирования может

воздействовать на объект с целью управления. Совокупность этих переменных

называют вектором регулирующих воздействий. Обычно регулирующими

воздействиями служат изменения расходов материальных потоков или потоков

энергии.

2. Переменные, изменение которых не связаны с воздействием системы

регулирования. Эти изменения отражают влияние на регулируемый объект внешних

условий, изменения характеристик самого объекта и т.п. Их называют

возмущающими воздействиями

В первую группу входных переменных необходимо включить Gt и Tt а во

вторую- CAвх, СBвх, Tвх

,Рt и Ра. Выходные переменные объекта - это те, значения которых вследствие

изменения входных переменных меняются. В нашем случае

таковыми являются СAвых, СBвых, СCвых, Gtвых, Тtвых, Твых.

Таким образом, химический реактор с мешалкой и рубашкой может быть

проиллюстрирован на рисунке 3.

Tt

Рис.3 Химический реактор с мешалкой и рубашкой как ОУ

3 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИНАМИКИ ОБЪЕКТА

УПРАВЛЕНИЯ

Запишем уравнение динамических режимов исследуемого объекта. Составим

соответствующие уравнения для каждой из входных переменных.

1) Покомпонентный материальный баланс в динамическом режиме получаем так:

[накопление комп. I] = [приход комп. I] –[ уход комп. I]

D(Са*V1)=G1вх*САвх*Dt- r *V1*Dt

Умножим это уравнение на 1/Dt и устремим Dt к нулю, при условии, что объем

смеси в аппарате остается постоянным V1=const, тогда имеем:

V1*dCА/dt=G1вх*САвх- r *V1 (1)

СА|t=0 =САBX

В уравнении (1) r- скорость накопления компонента, a [моль/(м3*с)].

Так как в нашем случае в реакторе протекает необратимая эндотермическая

реакция по схеме

А+ВС+DН

где k-константа скорости химической реакции

k=A*exp(-E/RT))

r=k*CА*СB,

r =-A *exp(-E/(R*T))*CА*CВ (1’)

Т.о. учитывая периодичность процесса и допуская что объем реактора

заполняется полностью за один цикл, получаем уравнение для вещества А:

dCА/dt= - A *exp(-E/(R*T))*CА*CВ (1’’)

Для компонента B и C по аналогии получим

dCB/dt= - A *exp(-E/(R*T))*CА*CВ (2’)

СВ½t=0 =СВBX

Для компонента С имеем:

dCC/dt= A *exp(-E/(R*T))*CА*CВ (3)

СС½t=0 =0

Здесь CА, CВ, CС – концентрации веществ А, В и С соответственно,[моль/м3]

Т- температура смеси на выходе, [0С].

А- тепловой множитель, [моль/с* м3]; Е- энергия активации,[ Дж/моль];

R=8,31 [Дж/моль*K] газовая постоянная;

2) Запишем тепловой (энергетический) баланс для объема реактора, учитывая,

что приход и уход компонентов отсутствует:

D(Cp1*r1*V1*Tвых)=K*S*(Tтвых

-Tвых)* Dt+DH* A *exp(-E/(R*T))*CА*CВ *V1

*Dt T½t=0 =TBX

(4) ,

где К- коэффициент теплопередачи [Дж/(м2*с*К)];

S-площадь боковой поверхности реактора,[м2];

Сp1-теплоемкость смеси [Дж/(кг*К)];

V1-объем реактора,[м3];

r1 – плотность смеси ,[кг/м3];

DH- энтальпия, [Дж/моль].

Преобразуем уравнение (4)

Cp1*r1*V1*dTвых/dt= K*S *(Tтвых-Tвых) +DH* A *exp(-E/(R*T))*CА*CВ *V1 (5)

T½t=0 =TBX

3) Запишем тепловой баланс для рубашки:

D(Cp2*r2*V2*Tтвых)=Gтвх*r2*Сp2*(Tтвх-Tтвых) *Dt-K*S*(Tтвых-Tвых)*Dt (6)

Tт½t=0 =Tт BX

Сp2-теплоемкость теплоносителя [Дж/(кг*К)];

V2-объем рубашки,[м3];

r2 – плотность теплоносителя, [кг/м3];

Gт – расход теплоносителя, [м3 /с].

Преобразуем уравнение (6)

Cp2*r2*V2*dTTвых/dt=GTвх*r2*Сp2 *(Tтвх-Tтвых) -K*S *(Tтвых-Tвых) (7)

Tт½t=0 =Tт BX

4) Материальный баланс для рубашки:

Запишем общий материальный баланс:

Gtвх=Gtвых

Gt=0.1*(kv1+kv2)*(ÖPt-Pa/r2 )/3600 (8)

где kv1 и kv2 – пропускная способность клапанов горячего и холодного

теплоносителя соответственно;

Pt- давление теплоносителя перед клапаном, Па;

Ра- давление теплоносителя в рубашке, Па.

Итак, имеются шесть уравнений для определения значений пяти выходных

переменных CА, СВ, CС, Tтвых, Tвых.

Таким образом, математическое описание динамики реактора с мешалкой и

рубашкой периодического действия представляет собой систему дифференциальных

уравнений (1), (2), (3), (5), (7), (8) с начальными условиями.

4 ИССЛЕДОВАНИЕ ДИНАМИКИ ОБЪЕКТА УПРАВЛЕНИЯ

Для получения некоторой переходной характеристики объекта необходимо каждый

раз решать систему уравнений, описывающую его динамику.

4.1 Переходные характеристики объекта в динамическом режиме.

Рис.4 Переходные характеристики Т(t), Tt(t) объекта при подаче горячего

теплоносителя в рубашку.

Рис. 5 Переходные характеристики СА(t), СВ(t), Сc

(t) объекта при подаче горячего теплоносителя в рубашку.

Программа, описывающая динамику ОУ, представлена в приложении А.

4.2 Переходная характеристика при входном воздействии в виде кусочно-линейной

зависимости

При получении переходной характеристики объекта по каналам Твх® С

Aвых, СBвых, СCвых,

Gtвых, Тtвых, Твых в случае, если на объект

действует ступенчатое воздействие, представленное на рис. 2, Полученная

переходная характеристика, построенная с помощью программы приведенной в

приложении Б, представлена на рис. 6

Рис. 6а Переходная характеристика объекта по каналам СAвых, СBвых, СCвых

в случае, если на объект действует ступенчатое возмущение.

рис. 6б Переходная характеристика объекта по каналам Твых , Тв , Тtвых

в случае, если на объект действует ступенчатое возмущение.

5 ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕСООВ ВАТОМАТИЧЕСКОЙ

СИСТЕМЕ РЕГУЛИРОВАНИЯ

Выбор структуры АСР

Для регулирования температуры смеси на выходе реактора, соответствующей

номинальному статическому режиму, можно изменять пропускную способность

клапанов горячего и холодного теплоносителей на входе в рубашку, подавая их

попеременно. Необходимо также подобрать оптимальные настройки регулятора, при

которых объект будет иметь характеристику, максимально приближенную к

заданному значению. В качестве чувствительного элемента введем датчик

температуры на выходе реактора. Структурная схема этой АСР представлена на

рис.7.

Рис. 7 Схема АСР температуры смеси на выходе из реактора

Для моделирования переходных процессов в АСР температуры смеси в реакторе,

необходимо иметь математическое описание этой системы регулирования.

Уравнение регулятора, в качестве которого в нашем случае выбран ПИ-регулятор

(объект инерционен), с введением динамической ошибки для заданной зоны

нечувствительности и в заданном диапазоне измерения температуры, выглядит

следующем образом:

Xp=Кp*E+1/TuòE*dt, где

E= Tизм- Tvx/Ео*100 – динамическая ошибка регулирования; Ео-размах шкалы;

Xp-отвечает за открытие клапанов и находится в пределах ограничения на

выходные значения выходного сигнала;

Кр- коэффициент передачи регулятора;

Ти- время изодрома [c];

Запишем уравнение для датчика температуры на выходе регулятора:

Td* dTизм /dt= -Tизм+T, где

Td-инерционность датчика, с;

Tизм- температура смеси, измеряемая датчиком на выходе;

T- температура смеси на выходе из реактора.

Для того, чтобы рассчитать переходной процесс в АСР температуры смеси в

реакторе, если на систему действует представленное на рис. 2 возмущающее

воздействие, была разработана программа (см. приложение В), при этом Твх

во времени изменялось в соответствии с заданием, а остальные входные переменные

задавались согласно номинальному статическому режиму.

На рис. 8а, 8б, 8в показаны переходные процессы при задающем воздействии

Tv(t), представленном на рис.2 с использованием ПИ-регулятора, а также

изменение регулирующего значения Xp во времени при оптимальных настройках

регулятора.

Рис 8а

Рис 8б

Рис 8в

Таким образом, исследовано динамическое поведение АСР температуры смеси на

выходе из ёмкости в различных ситуациях при различных параметрах настройки

регулятора, пропускной способности клапанов и законах регулирования. Это

дало определённую информацию о системе регулирования и позволило выявить её

характерные особенности.

ЗАКЛЮЧЕНИЕ

Основные результаты проведённых исследований состоят в следующем:

- проанализирован химический реактор с мешалкой и рубашкой

периодического действия как объект управления;

- разработано математическое описание динамики объекта;

- получены и проанализированы динамические характеристики СА

(t), СВ(t), Сc(t), Тт(t), Т(t) объекта;

- получена переходная характеристика по каналу передачи воздействия Т

вх®Т смеси в реакторе при подаче на объект заданного возмущения в виде

кусочно-постоянной функции;

- предложена структура АСР температуры смеси на выходе из реактора;

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1. Дудников Е.Г. Автоматическое управление в химической

промышленности. М.: Химия, 1987.-386с.

2. Кроу К., Гамилец А., Хоффман Т. Математическое моделирование

химических производств. М.: Мир, 1973.- 392 с.

3. Бояринов А.И., Кафаров В.В. Методы оптимизации в химической технологии.-

М.:Химия, 1969.-564с.

4. Стандарт предприятия. Проекты дипломные и курсовые. Правила оформления.

СТП ТИХМ 03-93.

5. Кулаков Ю.В., Шамкин В.Н. Математическое моделирование технологических

объектов и систем управления. Тамбов, 1997.-40с.

Приложение А

Программа описания динамики ОУ

dt=10;

tk=10000;

t=[0:dt:tk];

n=length(t);

% uravnenie materialnogo balansa dlya teplonositelya

kv1=1; % propusknaya sposobnost klapana goryachego teplonositelya

kv2=0; % propusknaya sposobnost klapana holodnogo teplonositelya

Pt=230000; % davlenie teplonositelya pered klapanom

Pa=101325; % davlenie teplonositelya v rubashke

ro2=1000; % plotnost teplonositelya

Gt=0.1*(kv1+kv2)*((Pt-Pa)/ro2)^0.5/3600; % rashod teplonositelya

N=zeros(1,n);

A=30; % koefficient

E=40000; % energia aktivacii

R=8.314; % gasovaya const

T=zeros(1,n); % temperatura smesi v reaktore

Tvh=15; % temperatura smesi na vhode v reaktor

ca=zeros(1,n);

cavh=20; % konzentraziya komponenta "A" na vxode v reaktor

cb=zeros(1,n);

cbvh=100; % konzentraziya komponenta "B" na vxode v reaktor

cc=zeros(1,n);

K=1000; % koefficient teploprovodnosti

d=1.0; % diametr reaktora

H=1.515; % visota reaktora

s=3.14*d*H; % ploshad bokovoj poverhnosti reaktora

Tt=zeros(1,n); % temperatura smesi teplonositela

Tt1=90; % temperatura teplonositelya 1 na vhode v rubashku

deltaH=10000; % teplovoi effekt reakcii

v1=3.14*H*d^2/4; % ob`em reaktora

ro1=800; % plotnost reakcionnoi massi

cp1=3500; % teploemkost smesi v reaktore

cp2=4100; % teploemkost teplonositelya

a1=1;

D=1.1;

v2=3.14*H*D^2/4-v1; % ob'em rubashki

% nachalnie uslovia

T(1,1)=Tvh; % temperatura smesi v reaktore

ca(1,1)=cavh; % konzentraziya komponenta "A" v reaktore

cb(1,1)=cbvh; % konzentraziya komponenta "B" v reaktore

cc(1,1)=0; % konzentraziya komponenta "C" v reaktore

Tt(1,1)=Tt1; % temperatura teplonositelya v rubashke

for i=2:n

% skorost reakcii

N(1,i)=A*exp(-E/(R*T(1,i-1)))*ca(1,i-1)*cb(1,i-1);

% pokomponentniy materialniy balans dlya reaktora

ca(1,i)=-N(1,i)*dt+ca(1,i-1); % konzentraziya komponenta "A" v reaktore

cb(1,i)=-N(1,i)*dt+cb(1,i-1); % konzentraziya komponenta "B" v reaktore

cc(1,i)=N(1,i)*dt+cc(1,i-1); % konzentraziya komponenta "C" v reaktore

% teplovoy balans (T-reaktor, Tt-rubashka)

T(1,i)=(K*s*(Tt(1,i-1)-T(1,i-1))+deltaH*N(1,i)*v1)*dt/(ro1*v1*cp1)+T(1,i-1);

Tt(1,i)=Tt(1,i-1)+dt*(Gt*ro2*cp2*a1*(Tt1-Tt(1,i-1))-K*s*(Tt(1,i-1)-T(1,i-

1)))/(ro2*v2*cp2);

end

% postroenie grafikov

figure(1)

plot(t,T,'b');

hold on;

plot(t,Tt,'r');

legend('T','Tt');

hold on;

grid on;

title('GRAFIKI TEMPERATUR');

figure(2)

plot(t,ca,'b');

hold on;

plot(t,cb,'r');

hold on;

plot(t,cc,'g');

legend('ca','cb','cc');

hold on;

grid on;

title('GRAFIKI KONCENTRACIY');

Приложение Б

Программа для построения переходных характеристик при кусочно-линейном

воздействии на объект в динамическом режиме

dt=1;

tk=10000;

t=[0:dt:tk];

n=length(t);

% uravnenie materialnogo balansa dlya teplonositelya

kv1=1; % propusknaya sposobnost klapana goryachego teplonositelya

kv2=0; % propusknaya sposobnost klapana holodnogo teplonositelya

Pt=230000; % davlenie teplonositelya pered klapanom

Pa=101325; % davlenie teplonositelya v rubashke

ro2=1000; % plotnost teplonositelya

Gt=0.1*(kv1+kv2)*((Pt-Pa)/ro2)^0.5/3600; % rashod teplonositelya

N=zeros(1,n);

A=30; % koefficient

E=4000; % energia aktivacii

R=8.314; % gasovaya const

T=zeros(1,n); % temperatura smesi v reaktore

Tvh=15; % temperatura smesi na vhode v reaktor

ca=zeros(1,n);

cavh=20; % konzentraziya komponenta "A" na vxode v reaktor

cb=zeros(1,n);

cbvh=100; % konzentraziya komponenta "B" na vxode v reaktor

cc=zeros(1,n);

K=1000; % koefficient teploprovodnosti

d=1.0; % diametr reaktora

H=1.515; % visota reaktora

s=3.14*d*H; % ploshad bokovoj poverhnosti reaktora

Tt=zeros(1,n); % temperatura smesi teplonositela

Tt1=90; % temperatura teplonositelya 1 na vhode v rubashku

Tt2=15; % temperatura teplonositelya 2 na vhode v rubashku

deltaH=10000; % teplovoi effekt reakcii

v1=3.14*H*d^2/4; % ob`em reaktora

ro1=800; % plotnost reakcionnoi massi

cp1=3500; % teploemkost smesi v reaktore

cp2=4100; % teploemkost teplonositelya

a1=0;

a2=1;

D=1.1;

v2=3.14*H*D^2/4-v1; % ob'em rubashki

% nachalnie uslovia

T(1,1)=Tvh; % temperatura smesi v reaktore

ca(1,1)=cavh; % konzentraziya komponenta "A" v reaktore

cb(1,1)=cbvh; % konzentraziya komponenta "B" v reaktore

cc(1,1)=0; % konzentraziya komponenta "C" v reaktore

Tt(1,1)=Tt1; % temperatura teplonositelya v rubashke

% zadanie vozmusheniya

Tv=zeros(1,n);

tau1=4000;

tau2=7500;

tau3=10000;

t1=[0:dt:tau1];

t2=[0:dt:tau2];

t3=[0:dt:tau3];

n1=length(t1);

n2=length(t2);

n3=length(t3);

for i=1:n1

Tv(i)=(45/4000)*i*dt+15;

end

for i=(n1+1):n2

Tv(i)=60;

end

for i=(n2+1):n3

Tv(i)=-0.008*i*dt+120;

end

for i=2:n

% skorost reakcii

N(1,i)=A*exp(-E/(R*T(1,i-1)))*ca(1,i-1)*cb(1,i-1);

% pokomponentniy materialniy balans dlya reaktora

ca(1,i)=-N(1,i)*dt+ca(1,i-1); % konzentraziya komponenta "A" v reaktore

cb(1,i)=-N(1,i)*dt+cb(1,i-1); % konzentraziya komponenta "B" v reaktore

cc(1,i)=N(1,i)*dt+cc(1,i-1); % konzentraziya komponenta "C" v reaktore

% teplovoy balans (T-reaktor, Tt-rubashka)

T(1,i)=(K*s*(Tt(1,i-1)-Tv(1,i-1))+deltaH*N(1,i)*v1)*dt/(ro1*v1*cp1)+T(1,i-1);

Tt(1,i)=Tt(1,i-1)+dt*(Gt*ro2*cp2*(a1*(Tt1-Tt(1,i-1))+a2*(Tt2-Tt(1,i-1)))-

K*s*(Tt(1,i-1)-Tv(1,i-1)))/(ro2*v2*cp2);

end

% postroenie grafikov

figure(1)

plot(t,T,'b');

hold on;

plot(t,Tt,'r');

hold on;

plot(t,Tv,'g');

legend('T','Tt','Tv');

hold on;

grid on;

title('GRAFIKI TEMPERATUR');

figure(2)

plot(t,ca,'b');

hold on;

plot(t,cb,'r');

hold on;

plot(t,cc,'g');

legend('ca','cb','cc');

hold on;

grid on;

title('GRAFIKI KONCENTRACIY');

Приложение В

Программа для построения переходных процессов в АСР температуры смеси на

выходе из реактора

dt=10;

tk=10000;

t=[0:dt:tk];

n=length(t);

% uravnenie materialnogo balansa dlya teplonositelya

kv1=10; % propusknaya sposobnost klapana goryachego teplonositelya

kv2=10; % propusknaya sposobnost klapana holodnogo teplonositelya

Pt=230000; % davlenie teplonositelya pered klapanom

Pa=101325; % davlenie teplonositelya v rubashke

ro2=1000; % plotnost teplonositelya

N=zeros(1,n);

A=30; % koefficient

E=4000; % energia aktivacii

R=8.314; % gasovaya const

T=zeros(1,n); % temperatura smesi v reaktore

Tvh=15; % temperatura smesi na vhode v reaktor

ca=zeros(1,n);

cavh=20; % konzentraziya komponenta "A" na vxode v reaktor

cb=zeros(1,n);

cbvh=100; % konzentraziya komponenta "B" na vxode v reaktor

cc=zeros(1,n);

K=1000; % koefficient teploprovodnosti

d=1.0; % diametr reaktora

H=1.515; % visota reaktora

s=3.14*d*H; % ploshad bokovoj poverhnosti reaktora

Tt=zeros(1,n); % temperatura smesi teplonositela

Tt1=90; % temperatura teplonositelya 1 na vhode v rubashku

Tt2=15; % temperatura teplonositelya 2 na vhode v rubashku

deltaH=10000; % teplovoi effekt reakcii

v1=3.14*H*d^2/4; % ob`em reaktora

ro1=800; % plotnost reakcionnoi massi

cp1=3500; % teploemkost smesi v reaktore

cp2=4100; % teploemkost teplonositelya

a1=0;

a2=1;

D=1.1;

v2=3.14*H*D^2/4-v1; % ob'em rubashki

en=zeros(1,n);

Tizm=zeros(1,n);

Tizm(1,1)=15;

Td=160;

del=2;

Kp=100;

Ti=500000;

sum=0;

Xpn=zeros(1,n);

% nachalnie uslovia

T(1,1)=Tvh; % temperatura smesi v reaktore

ca(1,1)=cavh; % konzentraziya komponenta "A" v reaktore

cb(1,1)=cbvh; % konzentraziya komponenta "B" v reaktore

cc(1,1)=0; % konzentraziya komponenta "C" v reaktore

Tt(1,1)=Tt1; % temperatura teplonositelya v rubashke

% zadanie vozmusheniya

Tv=zeros(1,n);

tau1=4000;

tau2=7500;

tau3=10000;

t1=[0:dt:tau1];

t2=[0:dt:tau2];

t3=[0:dt:tau3];

n1=length(t1);

n2=length(t2);

n3=length(t3);

for i=1:n1

Tv(i)=(45/4000)*i*dt+15;

end

for i=(n1+1):n2

Tv(i)=60;

end

for i=(n2+1):n3

Tv(i)=-0.008*i*dt+120;

end

for i=2:(n-1)

if i*dt >tau2

a1=0;

a2=1;

kv1=0;

kv2=16;

else a1=1;

a2=0;

kv1=16;

kv2=0;

end

if a2>0.5

e=(Tizm(1,i-1)-Tv(1,i-1))/120*100;

else

e=-(Tizm(1,i-1)-Tv(1,i-1))/120*100;

end

en(1,i-1)=e;

if abs(e)<del/2

e=0;

else e=(abs(e)-del/2)*sign(e);

end

Xp=Kp*e+sum*dt/Ti*Kp;

if Xp<0 Xp=0;

end

if Xp>100 Xp=100;

end

Xpn(1,i)=Xp;

% skorost reakcii

N(1,i)=A*exp(-E/(R*T(1,i-1)))*ca(1,i-1)*cb(1,i-1);

% pokomponentniy materialniy balans dlya reaktora

ca(1,i)=-N(1,i)*dt+ca(1,i-1); % konzentraziya komponenta "A" v reaktore

cb(1,i)=-N(1,i)*dt+cb(1,i-1); % konzentraziya komponenta "B" v reaktore

cc(1,i)=N(1,i)*dt+cc(1,i-1); % konzentraziya komponenta "C" v reaktore

% rashod teplonositelya

Gt=0.1*(kv1+kv2)*Xp/100*((Pt-Pa)/ro2)^0.5/3600; % rashod teplonositelya

% teplovoy balans (T-reaktor, Tt-rubashka)

T(1,i)=(K*s*(Tt(1,i-1)-T(1,i-1))+deltaH*N(1,i)*v1)*dt/(ro1*v1*cp1)+T(1,i-1);

Tt(1,i)=Tt(1,i-1)+dt*(Gt*ro2*cp2*(a1*(Tt1-Tt(1,i-1))+a2*(Tt2-Tt(1,i-1)))-

K*s*(Tt(1,i-1)-T(1,i-1)))/(ro2*v2*cp2);

% yravnenie datchica

Tizm(1,i)=(T(1,i-1)-Tizm(1,i-1))*dt/Td+Tizm(1,i-1);

sum=sum+e;

end

% postroenie grafikov

figure(1)

plot(t,T,'b');

hold on;

plot(t,Tt,'r');

hold on;

plot(t,Tv,'g');

hold on;

plot(t,en,'y');

hold on;

plot(t,Tizm,'m');

hold on;

legend('T','Tt','Tv','en','Tizm');

hold on;

grid on;

title('GRAFIKI TEMPERATUR');

figure(2)

plot(t,ca,'b');

hold on;

plot(t,cb,'r');

hold on;

plot(t,cc,'g');

legend('ca','cb','cc');

hold on;

grid on;

title('GRAFIKI KONCENTRACIY');

figure(3)

plot(t,Xpn,'m');

legend('Xpn');

hold on;

grid on;

title('REGULIROVANIE');