|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Курсовая: Создание простейшей нейросетиКурсовая: Создание простейшей нейросетиЭлементарная теория процесса обучения нейросетей Аннотация Задача представимости функции многих переменных в виде суперпозиции нескольких функций меньшего числа переменных поставленная еще Гильбертом получила новую жизнь благодаря теореме Хехт-Нильсена “об аппроксимации функции многих переменных двухслойной однородной нейросетью”. Нейросети на сегодняшний день являются важным инструментом при решении многих прикладных задач, а потому представляет большой интерес процесс обучения сетей. В работе сделана попытка анализировать этот процесс и представить его максимально просто и наглядно. Искусственные (формализованные) нейросети построены по схеме близкой к естественной нервной системе человека, т.е. достаточно простые структурные единицы, объединяясь в определенной последовательности, образуют сложную систему, способную решать огромные классы задач. Формализованный нейрон – это математическая модель естественного нейрона человека. Он включает в себя невырожденные линейные преобразования, а также некоторую нелинейную функцию, называемую функцией активации, как правило, сигмоидального типа: s =1/(1+ ехр(-a)) , (1) где s - непрерывная, всюду дифференцируемая возрастающая ограниченная функция. Графически формализованный нейрон (далее просто нейрон) показан на рис.1: Рис.1 Схема формализованного нейрона. Х1, Х2,., Хn - координаты входного вектора – исходная информация. Числа w1, w2,., wn – так называемые веса синапсов (входов нейрона) или сила связи данного входа с нейроном, b – дополнительный вход, называемый сдвигом, его значения, как правило, +1, 0. Знак S означает операцию линейных преобразований. Каждый вход умножается на соответствующий ему вес и все суммируется, далее полученная величина рассматривается как аргумент функции (1), значение значение которой является выходом нейрона. Искусственная нейросеть представляет из себя группу связанных определенным образом нейронов. Простейший случай – это однослойная нейросеть. Аналитически ее можно записать следующим образом: У= s(ХW), (2) где Х, Y – вектор-строки. Активационная функция многослойной сети должна быть нелинейной. Если эта функция будет линейной, легко показать, что любую многослойную сеть можно свести к однослойной. В однородной нейросети все нейроны по отдельности выполняют одинаковые функции. Основным существенным отличием их друг от друга являются веса синапсов, которые и играют главную роль в работе нейросетей. От правильного подбора весовых коэффициентов зависит, корректность работы сети. Процесс их подбора и называется обучением. Процесс обучения можно сравнить с настройкой. Известно 2 класса обучающих методов: детерминистские и стохастические. Детерминистский метод состоит в том, что шаг за шагом осуществляется процедура коррекции весов сети, основанная на использовании их текущих значений, а также величин входов и выходов (фактических и ожидаемых). Стохастические методы по определению предполагают выполнение псевдослучайных изменений, которые ведут к улучшению результата. Наиболее распространенным алгоритмом обучения нейросетей является алгоритм обратного распространения ошибки, основанный на методе градиентного спуска. Обучение при этом проходит в два этапа. Вначале сеть работает в обычном режиме, т.е. прямым потоком: на вход подаются начальные данные, и вычисляется вектор выхода. Затем находят функцию ошибки: где yj,p – реальная, а tj,p – ожидаемая j-тая координата выхода, при подаче на вход р-го образа. А уменьшают ее, напрявляя данные по сети в обратном порядке, работа проходит через определенные этапы следующим образом: 1. Подача на вход сети один из возможных образов и в режиме обычного функционирования нейросети, когда сигнал распространяется от входа к выходу, рассчет значения последнего. 2. Рассчет ошибок dN и DwN слоя N. 3. Рассчет ошибок dn и Dwn для всех остальных слоев, n=N-1,.,1. 4. Корректировка всех весов в сети. 5. Проверка ошибки сети и переход на шаг 1 или в конец. Сети на шаге 1 попеременно в случайном порядке предъявляются все образы из обучающего множества, чтобы сеть не “забывала” одни по мере “запоминания” других. Этот алгоритм, после предварительной подготовки, может быть представлен более наглядно и интерпретирован геометрически. Пусть Еn – n-мерное евклидово пространство. Множества Х, Y, Т – области пространства Еn – множества векторов. Причем, такие что " ÎХ $! соответствующий ему вектор ÎT. Y такое что где G принадлежит пространству непрерывных операторов. Пусть W - пространство матриц n´n dim=2, где wÎW рассматривается как совокупность вектор-строк, составляющих матрицу w: (w21 w22 .w2n) (5) ... (wn1 wn2 .wnn) Это делается для геометрической представимости. Определим вид оператора G½ G: X®Y. Этот оператор есть ни что иное как суперпозиция двух операторов G = S °s. Рассмотрим подробнее каждый из составляющих операторов: 1. Первый оператор: S = wх (6) Оператор линейных преобразований, где wÎW, x – вектор-столбец из X, S – результат умножения – вектор-строка. В развернутом виде матричное умножение выглядит следующим образом: (w21 w22 .w2n) ´ х2 =||(w11x1+.+w1nxn).(wn1x1+.+wnnxn)|| =S (7) ... : (wn1 wn2 .wnn) хn Т.е. 2. Второй оператор - нелинейная функция. Функция s (см. формулу (1)) называется также сжимающей. Для последующих операций нормализуем вектора множества Х: х¢ = х/|х|, где |х| = , х¢ - нормализованный вектор. Аналогичную операцию произведем над множеством Т. Поскольку wÎW совокупность вектор-строк, нормализуем и эти вектора: wi : wi = (wi1 wi2 . win ), wi¢ = wi /|wi|. После нормализации векторов х и wi, вектор S изменит свой вид: 1/ |wi||x| = ki =Const. Таким образом, нормализация векторов х и wi лишь сжимает вектор S , но не меняет его направления. Для простоты обозначений, заменим вновь полученные вектора х¢, t¢, wi¢ и S* соответственно на х, t, w и S. В результате всех преобразований будем иметь радиус-векторы единичной n-мерной сферы. Пусть для наглядности n =2, тогда весь процесс можно представить геометрически. Т т s w1 w1 х х w2 w2 a. b. Рис.2 Радиус-векторы единичной n-мерной сферы, полученные после нормализации векторов из множеств X, W, T (a). Векторы S и Y, полученные после всех преобразований (b). Х и t – взаимнооднозначная пара векторов из множеств Х и Т соответственно, эта пара называется обучающей. Кроме того, вектору х соответствует также вектор уÎY, полученный “экспериментально”, путем применения изложенных выше преобразований. Задача обучения состоит в том, чтобы преобразования эти были таковы, что у = t, "уÎY, tÎT. А это значит, что все координаты уj вектора у должны быть равны одноименным коорданатам вектора t. Теперь, после того как все вектора нормализовали линейное преобразование (6) будет иметь вид: Si = Si – это фактически скалярное произведение векторов wi и x: Si =(wi,х)=|wi||х| Cos ai , (9) где ai – плоский угол между х и wi. Поскольку, |wi|=|х|=1, то Si= Cos ai (10) Таким образом, вектор S – это вектор, все координаты которого Cos a i, i=1,.n, а |S|£ Ön. Получили вектор S, подставим его в (1) покоординатно в функцию s. Покажем, что векторы S и у лежат на одной прямой. Имеем у= 1/ (1+exp(-s)), Ехр(-s)=1+(-s)+1/2!(-s)² +1/3!(-s)² (-s)+. т.е. разложили экспаненту в ряд по степеням (-s). Этот ряд сходится, разобьем его на два подряда, которые также будут иметь предел, как части сходящегося ряда: Ехр(-s)= Первое слагаемое есть Const=C0(s) (за счет четных степеней), а второе слагаемое –C2(s)s. Получили ехр(-s)=C0(s)-C2(s )s, поскольку в знаменателе есть еще единица, прибавим ее к C0, получим C0(s)+1=C1(s). Итак, имеем: Y=1/(C1(s)-C2(s) Вектор, находящийся в знаменателе - n = C1(s)-C2(s) , лежит на одной прямой с вектором S. Получили (у, n )=1, а это (в случае, если оба вектора имеют единичную длину, либо длины их взаимнообратные величины, что также возможно) озночает, что вектора у и n совпадают по направлению, т.е. вектор у лежит на одной прямой с вектором S. Таким образом процесс обучения нейросети сводится к “подгону” вектора S под вектор T за счет измнения углов между векторами х и wi (рис.2 (b)), поскольку было показано, что координаты вектора S есть ни что иное, как косинусы этих углов. На сегодняшний день аппарат нейросетей используется практически во всех областях науки, экономики и т.д. Программа нейротомографии была применена к эксперсс-томографии осесимметричных объектов, которые были изучены с помощью дискретного моделирования. Результаты работы нейротомографии сравнивались с результатами, полученными в ходе вычислительного эксперимента. Соответствие между экспериментом нейротомографии и прямого вычислительного эксперимента оценивались по различным параметрам правдоподобия. Рис.3 В данном случае нейротомография используется для реконструкции различных осесимметричных объектов (b) по единственной радоновской проекции R(s). На (c) дано сравнение истинного (a) с восстановленным (b). Было установлено, что нейротомография может быть использована эффективно для решения различных задач томографии. |
|

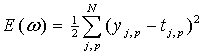 , (3)
, (3) (w11 w12 .w1n)
(w11 w12 .w1n) (w11 w12 . w1n) х1
(w11 w12 . w1n) х1