|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Контрольная работа: Вычисление показателей вариацииКонтрольная работа: Вычисление показателей вариацииКонтрольная работа по курсу: Статистика Раздел "Общая теория статистики" Задача 1
Решение. Признаком в данной задаче является общий стаж рабочего, а частотами соответственно количество рабочих, имеющих тот или иной стаж. Ряд распределения - интервальный, причем первый и последний интервал - открытые. Если интервалы открыты, то по правилам принимаем величину первого интервала равной второму, а последнего предпоследнему. Так как имеются и значения признака и частоты, то средний стаж находим по формуле средней арифметической взвешенной. А так как ряд интервальный, то в качестве значения признака в каждой группе берём середины интервала
Для решения задачи и вычисления заданных показателей, построим вспомогательную таблицу.
Среднюю заработную плату по каждой группе и для всех рабочих определяем по формуле средней арифметической простой:
Задача 2Решение: 1) Вычислим средний процент выполнения плана по выпуску продукции
2) Абсолютный прирост показывает насколько изменился текущий уровень по сравнению с предыдущим или базисным и определяется как разность двух уровней
∆3=630,0 - 510,0 =120,0 Задача 3Решение. В задаче значения
признака имеют различную численность, поэтому значения,
а) Среднее время горения электролампы определяется по формуле
б) Дисперсия, взвешенная по частоте вариантов, равна
Среднее квадратичное отклонение равно:
2) коэффициент вариации составляет
3) Решение. Для определения моды определяем модальный интервал. Им является интервал 25-30 лет, так как его частота наибольшая (1054), тогда Мо Для определения медианы тоже необходимо определить медианный интервал. Медианным интервалом является интервал 4000-4500, так как он является первым интервалом, накопленная частота которого превышает полусумму частот (100: 2=50). Тогда медиана определится как: Ме Задача 4Решение. Абсолютный прирост показывает, насколько изменился текущий уровень по сравнению с предыдущим или базисным и определяется как разность двух уровней
Темп роста показывает, во сколько раз текущий уровень больше предыдущего или базисного, и определяется как отношение двух уровней, выраженное в процентах:
Темп прироста показывает, на сколько процентов увеличился текущий уровень по сравнению с текущим или базисным и определяется как разность соответствующего темпа роста и 100%:
Абсолютное значение 1% прироста определяется как отношение абсолютного прироста к темпу прироста:
Среднегодовой темп роста рассчитывается по формуле средней геометрической
Среднегодовой темп прироста равен среднегодовому темпу роста минус 100%, т.е.1,12% - 100% = - 98,88%
Среднегодовой абсолютный прирост исчисляется по формуле средней арифметической простой и равен
Среднегодовой абсолютный прирост можно вычислить и таким образом:
Начальный уровень (величина первого члена ряда) - 4140, конечный - 5426. Средний уровень ряда определяется по формуле простой средней арифметической, так как ряд периодический
Задача 5Решение. Решение. Рассчитываем индекс физического объема: Iq=
Рассчитываем индекс себестоимости объема: Ip=
Агрегатные индексы затрат на производство продукции, себестоимости и физического объема: Iq=
Ip=
Средние затраты рассчитываем при помощи средней арифметической взвешенной, затем найдем индекс переменного состава: In. c=
Динамика средней себестоимости складывается под влиянием двух факторов: изменения себестоимости на отдельных предприятиях и от структуры производства продукции отрасли. Рассчитаем индекс себестоимости постоянного состава: Iср. с=
Таким образом, в результате повышения себестоимости единицы продукции на обоих предприятиях средняя цена выросла на 18,7% Определим влияние на среднюю цену структурных сдвигов: Iстр. сдв=
За изучаемый период, структура производства практически не изменилась, поэтому изменение средней цены произошло целиком за счет влияния первого фактора, т. е изменения себестоимости на производство продукции на каждом предприятии. Правильность расчетов подтверждает проверка через взаимосвязь индексов In. c=Iф. с*Iстр. сдв=1,187*1=1,187 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

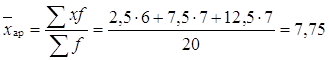
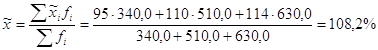 .
.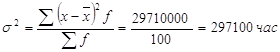 2.
2.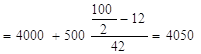 час
час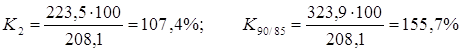 .
.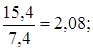 и т.д.
и т.д.
