|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Курсовая работа: Экономико-математические методы анализаКурсовая работа: Экономико-математические методы анализаВВЕДЕНИЕ. Одним из направлений совершенствования анализа хозяйственной деятельности является внедрение экономико-математических методов и современных ЭВМ. Их применение повышает эффективность экономического анализа за счет расширения факторов, обоснования принимаемых управленческих решений, выбора оптимального варианта использования хозяйственных ресурсов, выявления и мобилизации резервов повышения эффективности производства. Математические методы опираются на методологию экономико-математического моделирования и научно обоснованную классификацию задач анализа хозяйственной деятельности. В зависимости от целей экономического анализа различают следующие экономико-математические модели: в детерминированных моделях логарифмирование, долевое участие, дифференцирование; в стохастических моделях корреляционно-регрессивный метод, линейное программирование, теорию массового обслуживания, теорию графов. СТОХАСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И АНАЛИЗ ФАКТОРНЫХ СИСТЕМ ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ. Стохастический анализ – это метод решения широкого класса задач статистического оценивания. Он предполагает изучение массовых эмпирических данных путем построения моделей изменения показателей за счет факторов, не находящихся в прямых связях, в прямой взаимозависимости и взаимообусловленности. Стохастическая связь существует между случайными величинами и проявляется в том, что при изменении одной из них меняется закон распределения другой. Так если случайная величина Х- функция двух групп случайных величин Z и v, X=f(Z1, Z2, ..., Zn; v1, v2, ...,vn), а случайная величина Y – функция двух групп случайных величин Y=Y(Z1, Z2, ..., Zn; v1, v2, ..., vn), то между X и Y есть стохастическая связь. В основе построения стохастических моделей лежит обобщение закономерностей варьирования значений изучаемых экономических показателей. Предпосылкой для применения стохастического подхода моделирования связей служит качественная однородность совокупности (относительно изучаемых связей) и варьирования признаков по хозяйственным объектам и периодам. Стохастическое моделирование можно применять в анализе хозяйственной деятельности, если есть возможность составить совокупность наблюдений. Моделирование ведется методами математической статистики, которые позволяют исследовать опосредованные причинно-следственные связи показателей производственно-хозяйственной деятельности с факторами и условиями производства. Детерминированное моделирование в данном случае не всегда возможно. С помощью математико-статистических приемов можно обойтись без специальных экспериментов. В экономическом анализе выделяются следующие наиболее типичные задачи стохастического анализа: · изучение наличия и тесноты связей между функцией и факторами, а также между факторами; · ранжирование и классификация факторов экономических явлений; · выявление аналитической формы связи между изучаемыми явлениями; · сглаживание динамики изменения уровня показателей; · изучение размерности (сложности, многогранности) экономических явлений; · количественное изменение информативных показателей; · количественное изменение влияния факторов на изменение анализируемых показателей (экономическая интерпретация полученных управлений). Стохастическое моделирование и анализ связей между изученными показателями начинаются с корреляционного анализа. Корреляция состоит в том, что средняя величина одного из признаков изменяется в зависимости от значения другого. Признак, от которого зависит другой признак, принято называть факторным. Зависимый признак именуют результативным. В каждом конкретном случае для установления факторного и результативного признаков в неодинаковых совокупностях необходим анализ природы связи. Так, при анализе различных признаков в одной совокупности заработная плата рабочих в связи с их производственным стажем выступает как результативный признак, а в связи с показателями жизненного уровня или культурными потребностями – как факторный. Часто зависимости рассматривают не от одного факторного признака, а от нескольких. Для этого применяется совокупность методов и приемов выявления и количественной оценки взаимосвязей и взаимностей между признаками. При исследовании массовых общественно-экономических явлений между факторными признаками проявляется корреляционная связь, при которой на величину результативного признака влияет, помимо факторного, множество других признаков, действующих в разных направлениях одновременно или последовательно. Часто корреляционную связь называют неполной статистической или частичной в отличие от функциональной, которая выражается в том, что при определенном значении переменной (независимая переменная – аргумент) другая (зависимая переменная – функция) принимает строгое значение. Корреляционную связь можно выявить только в виде общей тенденции при массовом сопоставлении фактов. Каждому значению факторного признака будет соответствовать не одно значение результативного признака, а их совокупность. В этом случае для вскрытия связи необходимо найти среднее значение результативного признака, а их совокупность. В этом случае для вскрытия связи необходимо найти среднее значение результативного признака для каждого значения факторного. Проблема измерения связи имеет две стороны: выяснение формы и тесноты. При определение формы связи выявляется изменение средней величины результативного признака в зависимости от изменения факторного. Выбор тех или иных показателей тесноты корреляционной связи зависит от ее формы. Под формой связи понимают тип аналитической формулы, выражающей зависимость между рассматриваемыми признаками. Различают связь прямую, при которой с ростом (снижением) факторного признака у результативного обнаруживается тенденции к увеличению (уменьшению), и обратную, когда с увеличением (уменьшением) факторного признака результативный снижается (увеличивается). Форма корреляционной зависимости характеризует тенденцию, проявляющуюся в изменениях рассматриваемого признака с изменением признака-фактора. Если наблюдается тенденция равномерного возрастания или убываний значений признака, то зависимость называется прямолинейной, в противном случае – криволинейной. Уравнивание корреляционной связи (уравнение регрессии) – аналитическое. С его помощью выражается связь между признаками (иногда форма связи). Различают прямолинейное (прямая линия) и криволинейное (парабола, гипербола) уравнения. Линии на графиках, изображающие тенденции в изменения признака, коррелируемого с признаком-фактором, называются линиями регрессии. В них находит графическое выражение форма связи. При использовании корреляционно-регрессивного приема анализа модель изображается в виде уравнения регрессии типа y=f(x), где у – зависимая переменная (результативный признак или функция от ряда факторов-аргументов);х – независимые переменные (факторы-аргументы). Парной корреляцией называется корреляционная зависимость между двумя признаками. Простейшим уравнением, характеризующим прямолинейную зависимость между двумя признаками, служит уравнение прямой линии: Y = a + bx, где х и у(х) – соответственно независимый и зависимый признак; a и b – параметры уравнения.
Количество наблюдений при прямолинейной
В качестве примера прямолинейной зависимости
и производительности труда (табл. 1.1.)
При планировании производительности труда важно установить темпы ее роста в зависимости от увеличения фондовооруженности. Связь между
производительностью и фондовооруженностью труда можно выразить в виде
уравнения прямой линии: Для выяснения связи
рассчитаем коэффициент корреляции по формуле: Если коэффициент корреляции равен 1, значит, результативный признак полностью зависит от признака-фактора, т. е. по существу корреляционная зависимость совпадает с функциональной. Следовательно, чем ближе коэффициент корреляции к 1, тем теснее связь между явлениями и наоборот. Для нахождения
неизвестных параметров a и b решим систему так называемых
нормальных уравнений: Для исчисления величины Числовые значения ху,
х, у, В результате подстановки данных в систему уравнений получаем: 80,9 = 10а + 22,6b; 188,4 = 22,6а + 52,6b. Отсюда а = +6,7; b = 0,912. Значит, уравнение, представляющее связь между фондовооруженностью и производительностью труда работающих, имеет вид у(х) = 6,7 + 0,912х. Следовательно повышение фондовооруженности труда на 1000 руб. приводит к росту его производительности на 912 руб. Эти данные учитываются при перспективном и текущем планировании роста производительности труда. Использование
множественной корреляции в экономическом анализе. В зависимости от количества
отобранных факторов различают парные и многофакторные модели. Из многофакторных
используется: линейные В экономических расчетах предпочтение отдается линейным моделям, что обусловлено следующими причинами: 1.Относительная простота и меньший объем вычислений ; 2.Массовые экономические процессы, как правило, подчиняются закону нормального распределения, которому свойственны линейные формы связи. Факторы, включаемые в корреляционно-регрессивную модель, отбираются в несколько приемов: логический отбор в соответствии с экономическим содержанием; отбор существенных факторов по оценки их значимости по t-критерию Стьюдента либо F-критерию Фишера; последовательный отсев незначимых факторов. При расчетах множественной корреляции применяется степень точности 5%, что соответствует вероятности Р=0,05. Корреляция рядов динамики имеет некоторые особенности. Кроме кратковременных колебаний (годовых, квартальных, месячных), в ряду имеется еще один компонент – общая тенденция в изменения показателей ряда (тренд). При этом имеет место автокорреляция зависимость между последовательными (то есть соседними) значениями уровней динамического ряда. Для проверки наличия
автокорреляции в динамических рядах вычисляется критерий Дарбина – Уотсона Для определения выровненного ряда (тренда) с целью его последующего исключения чаще всего прибегают к механическому сглаживанию и аналитическому выравниванию методом наименьших квадратов. Механическое сглаживание ведется с помощью скользящей, или подвижной средней. Этот способ состоит в вычислении каждой новой средней одного члена ряда слева и присоединении одного члена ряда слева и одного справа. Кроме статистических характеристик (Табл.1.2) рассчитываются также их ошибки. Величина ошибки отражает диапазон, в котором находится та или иная статистическая характеристика.
Матрица коэффициентов парной корреляции. Для измерения тесноты связи между факторами и результативным показателем исчисляют парные, частные и множественные коэффициенты корреляции. Они обладают следующими свойствами: -1 ≤ r ≤1; если r = 0, линейная корреляционная связь отсутствует; если [r] = 1, между переменными х и у существует функциональная зависимость; связь считается сильной, если [r] ≥ 0,7. При [r] ≤ 0,3 – связь слабая. Парные коэффициенты рассчитываются для всевозможных пар переменных без учета влияния других факторов. Чтобы учесть взаимное влияние факторов, исчисляются частые коэффициенты, которые отличаются от первых тем, что выражают тесноту корреляционной зависимости между двумя признаками при устранении изменений, вызванных влиянием других факторов модели. Матрица критериев некоррелированности необходима для выбора наиболее значимых факторов, чье совместное влияние формирует его величину. При этом исключению обычно подлежат факторы, которые при парном коррелировании друг с другом дают высокий линейный коэффициент, превышающий по абсолютной величине 0,85. Наличие такой связи между двумя факторами называют коррелиарностью, а между несколькими мультиколлинеарностью. На основании данных матрицы машина отвергает или не отвергает гипотезу о мультиколлинеарности. Коэффициенты множественной детерминации представляют собой квадрат коэффициента корреляции. Он показывает, на сколько процентов вариация результативного показателя зависит от влияния избранных факторов. Вектор значений Фишера используется для оценки множественного коэффициента корреляции и уравнения регрессии. Расчетные значения вектора значений сравниваются с табличными. Для оценки значимости факторов необходима матрица значений распределения Стьюдента. Расчетные значения здесь также сравниваются с табличными. После этого начинается шаговый регрессивный анализ. Его результатом становится уравнение регрессии
где а0 – свободный член уравнения; х1,х2,…,хn – факторы, определяющие результатный показатель в его единицах измерения. Далее следует группа оценочных показателей уравнения регрессии в целом: F – отношение Фишера для оценки
множественного коэффициента корреляции и уравнения регрессии в целом; dэ –отношение Дарбина – Уотсона для определения наличия автокорреляции
в рядах динамики; э – коэффициент эластичности – отношение изменения ( в процентах)
одного признака при изменении на 1% другого. Для f(x)
коэффициент эластичности обращается в э = Интерпретацию выходной информации можно последить на примере корреляционного анализа фондоотдачи. Для построения на первом этапе отобраны следующие факторы: Х1 – удельный вес машин и оборудования в общей стоимости основных производственных фондов, %; Х2 – электрооворуженность рабочих, тыс. кВт∙ч; Х3 – уровень использования производственной мощности, %. Числовые характеристики анализируемых показателей представлены в таблице 1.3.
Данные таблицы показывают, что незначительным колебаниям подвержены факторы Х3 и Х1; средняя колеблемость присуща функции Y, значительная – фактору Х2. Однако коэффициенты вариации показателей не превышают 33%, что свидетельствует об однородности исходной информации.
Коэффициенты асимметрии говорят о правосторонней асимметрии распределения рядов Х1 и Х3 и о левостороннем распределении рядов Х2 и У. Величина эксцесса для всех показателей не превышает 3, что подтверждает низковершинное распределение вариационных рядов. Указанные коэффициенты интерпретируются геометрически. Далее анализируется матрица коэффициентов парной корреляции (табл. 1.5.).
В данном примере наиболее тесная связь наблюдается между показателями фондоотдачи (У), идеального веса активной части фондов (Х1) и уровня загрузки производственной мощности (Х3). Парные коэффициенты корреляции соответственно составили 0,937778 и 0,92272. Расчет парных коэффициентов корреляции выявил слабую связь фондоотдачи с электровооруженностью труда Х2 – 0,09361. Гипотеза о наличии мультиколлинеарности отвергается, т. е. все показатели относительно независимы. Для рассматриваемого примера вектор коэффициентов множественной детерминации равен: У = 0,9002; Х1 = 0,9043; Х2 = 0,0100; Х3 = 0,8820. Вектор интерпретируется следующим образом: изменение (вариация) функции (У) на 90,02% зависит от изменения избранных факторов-аргументов; фактора Х1 – на 90,43% от изменения функции (У) и остальных факторов и т. д. В таблице 1.6. приведены частные коэффициенты корреляции. Они показывают связь каждой пары факторов в чистом виде при неизменном значении остальных параметров.
Частные коэффициенты корреляции ниже парных. Это говорит о том, что чистое влияние факторов слабее, чем влияние оказываемое отдельными факторами во взаимодействии с остальными. Статистическая значимость, надежность связи, выраженная частными коэффициентами корреляции, проверяется по t-критерию Стьюдента путем сравнения расчетного значения с табличными при заданной степени точности (Табл. 1.7.).
Обычно в практике экономических расчетов степень точности берется равной 5%, что соответствует вероятности р = 0,05. В таблице приведены критические значения t-критерия Стьюдента для вероятности р = 0,05 и 0,01 при различном числе степеней свободы, которые определяются как (n–1), где n – число наблюдений. В нашем примере при числе степеней свободы 40 – 1 = 39 табличное значение tтабл. = 2,021. Расчетные значения t-критерия (первая графа таблицы) для факторов Х1 и Х3 оказались выше табличных, что свидетельствует о значимости этих факторов для анализируемой функции. Фактор Х2 как незначимый для функции должен быть исключен из дальнейших расчетов. Далее на ЭВМ проводится шаговый анализ с постепенным включением в модель избранных факторов по критерию значимости. На каждом шаге рассматриваются уравнения регрессии, коэффициенты корреляции и детерминации, F-критерий, стандартная ошибка оценки и другие показатели. После каждого шага перечисленные оценочные показатели сравниваются с рассчитанными на предыдущем шаге. Уравнение регрессии будет тем точнее, чем ниже величина стандартной ошибки (табл. 1.8.).
Если добавление последующих факторов не улучшает оценочные показатели, а иногда и ухудшает их, необходимо остановиться на том шаге, где показатели наиболее оптимальны. Результаты шагового анализа представлены в Табл. 1.8. свидетельствуют о том, что сложившиеся взаимосвязи наиболее полно описывает двухфакторная модель, полученная на втором шаге: у = У = -3,085 = 0,0774 Х1 + 0,0234 Х3. Статистический анализ данного уравнения регрессии подтверждает, что оно значимо: фактическое значение F-критерия Фишера равно 166,7, что значительно превышает Fтабл. = 3,25. Табличное значение F-критерия находится по заданной вероятности (р = 0,95) и числе степеней свободы для столбца таблицы (m – 1), где m – число параметров уравнения регрессии, включая свободный член, и для строки таблицы (n – m), где n – число наблюдений. Например F-табличное находится на пересечении столбца 2 (3 – 1) и строки 37 (40 – 3) и равно 3,25 (Табл. 1.9.). Коэффициент множественной корреляции, равный 0,9488, свидетельствует о тесной взаимосвязи между фондоотдачей и удельным весом активной части основных фондов, а также уровнем использования производственной мощности. Величина коэффициента множественной детерминации 0,9001 свидетельствует о том, что изменение детерминации на 90,01% зависит от изменения учтенных факторов. Параметры уравнения регрессии интерпретируется следующим образом: коэффициент регрессии при Х1 (0,0774) показывает, что увеличение удельного веса машин и оборудования в общей стоимости основных производственных фондов на 1% ведет к росту фондоотдачи на 7,74 копейки. Повышение уровня загрузки мощностей на 1% поднимает фондоотдачу на 2,34 копейки.
В случае обратной связи, т.е. при уменьшении изучаемой функции в связи с ростом фактора-аргумента, коэффициент регрессии имеет знак «минус». Свободный член уравнения ао = -3,085 экономически не интерпретируется. Он определяет положение начальной точки линии регрессии в системе координат. Численное значение коэффициентов эластичности отражает, на сколько процентов изменится функция при изменении данного фактора на 1% (имеется в в иду относительный прирост, а не абсолютный) приведет к росту фондоотдачи на 1,65%; улучшение уровня использования мощности на 1% повысит фондоотдачу на 1,3%. По абсолютной величине бета-коэффициентов можно судить о том, в какой последовательности находятся факторы по реальной возможности улучшения функции. Для нашего примера последовательность переменных выглядит следующим образом:
Отношение Дарбина (коэффициент Дарбина – Уотсона) равно 1,215. Значит, в рядах динамики имеется автокорреляция. Заключительную матрицу данных полностью характеризуют соответствующие заготовки (по столбцам): 1. У – фактическое. 2. У – расчетное. 3. Отклонение (Уфакт – Урасч). 4. Доверительные интервалы (границы, выход за пределы которых имеет незначительную вероятность). Для устранения автокорреляции модель пересчитана по приростным величинам. В результате получено следующее уравнение регрессии: У = -0,0079 + 0,0345; Х3 + 0,0475 Х1. Оно значимо: величина F-критерия равна 178,3. Коэффициент Дарбина составляет 2,48, т.е. близок к 2, что говорит об отсутствии автокорреляции. Коэффициент множественной корреляции (0,9518) выше, чем рассчитанный в первом случае. Величина коэффициента множественной детерминации также выше (0,9060). В окончательном виде уравнение регрессии интерпретируется таким образом: повышение уровня загрузки (производственной мощности) на 1% приведут к росту фондоотдачи на 3,45 копейки, а удельного веса машин и оборудования в общей стоимости основных производственных фондов – на 4,75 копейки. Справочный материал. Обработка данных при постановлении множественных моделей корреляционно-регрессивной зависимости производится на ЭВМ по типовой программе. Исходные данные должны быть достоверны, экономически интерпретируемы, количественно соизмеримы. Расчеты оформляются в виде таблице, в которой первая графа отражает число наблюдений n, вторая (у) – результативный показатель, каждая следующая (х) – факторы в любом порядке, так как факторы машина вводит в процессе шагового анализа по значимости критерия. При заполнении таблицы исходных данных следует указывать одинаковое количество знаков после запятой в пределах одной графы. Для предотвращения ошибок необходимо использовать данные с возможно большим числом значащих цифр (не менее 5). Процентные отношения требуется давать с точностью до 0,001. В таблице 1.10. приведены значения F-критерия для р = 0,95 в зависимости от числа степеней свободы: (m–1) – для столбца и (n–m) для строки, где m – число параметров уравнения регрессии, включая свободный член; n – число наблюдений.
МЕТОД ДИСКОНТИРОВАНИЯ. Дисконтирование – это процесс пересчета будущей стоимости капитала, денежных потоков или чистого дохода в настоящую. Ставка по которой производится дисконтирование, называется ставкой дисконтирования (ставкой дисконта). Основная посылка, лежащая в основе понятия дисконтированного потока реальных денег, состоит в том, что деньги имеют временную цену, т. е. сумма денег, имеющаяся в наличии в настоящее время, обладает большой ценностью, чем такая же сумма в будущем. Эта разница может быть выражена как процентная ставка (р), характеризующая относительные изменения за определенный период (обычно равный году). Предположим, что Ф(t) – номинальная цена будущего потока реальных денег в году t и Ф(0) – цена этого ожидаемого притока или оттока в настоящее время (текущая цена). Тогда (предполагая, что р – постоянная величина)
Смысл проведения расчетов методом дисконтирования состоит в том, чтобы определить сумму, которую следует заплатить сегодня с тем, чтобы получить планируемую отдачу от инвестиций в будущем. Для применения метода дисконтирования об объекте инвестирования необходимо знать следующие исходные данные: величиной инвестиции, планируемые величины денежных потоков или чистого дохода, норма дисконтирования, срок проекта. При расчете денежных притоков и оттоков (кеш-фло) учитывается не только поступления денежных средств от операционной и инвестиционной деятельности, но и потоки от финансовых результатов. Чистый поток наличности (ЧПН) определяется как разность между притоками и оттоками наличности от операционной (производственной) и инвестиционной деятельности минус издержки по финансированию проекта. Чистый дисконтированный доход (ЧДД) определяется как сумма ЧПН за расчетный период. Пример расчета куммулятивного
ЧДД приведен в приложении 1. Здесь куммулятивный чистый поток реальных денег
(строка 9) рассчитывается сложением куммулятивного чистого потока реальных
денег за предыдущий период и чистого потока реальных денег за отчетный год.
Например, куммулятивный чистый поток реальных денег в 2002 (5-м) году равен
8300 млн. руб. (-10000 + 1700). ЧДД (строка 10)рассчитывается по формуле ЧД = строка
8 / Коэффициент дисконтирования для приведения чистых денежных потоков к начальному периоду определяется по формуле
где Д – ставка дисконтирования (норма дисконта); t год, за который дисконтируется чистый доход, начиная с момента инвестирования. Значение коэффициентов
дисконтирования Норма дисконта отражать прибыль инвестора, которую он мог бы получить при инвестициях в другой проект. Она является минимальной нормой прибыли, ниже которой инвестор счел бы свои вложения не выгодными. ЧДД характеризует интегральный эффект от реализации проекта и определяется как величина, полученная дисконтированием разницы между всеми готовыми оттоками и притоками реальных денег, накапливаемых в течении горизонта расчета проекта Т (при постоянной ставке процента отдельно для каждого года):
где Формулу для расчета ЧДД можно представить в следующем виде: ЧДД = П(0) + П(1) ∙ К1 + П(2) ∙ К2 + … + П(Т) ∙ Кt. Чистый дисконтированный доход как критерий для оценки эффективности инвестиций достаточно корректен и экономически обоснован. Во-первых, ЧДД учитывает изменение стоимости денег во времени. Во-вторых, ЧДД зависит только от прогнозируемого чистого денежного потока и альтернативной стоимости капитала. В-третьих, ЧДД имеет свойство аддитивности, т. е. ЧДД нескольких инвестиционных проектов можно складывать, так как все они выражены в сегодняшних деньгах. ОПТИМИЗАЦИОННЫЕ МЕТОДЫ АНАЛИЗА И ПРИНЯТИЯ РЕШЕНИЯ В ЭКОНОМИКЕ. Многие задачи, с которыми приходится сталкивается экономисту в повседневной практике при анализе хозяйственной деятельности предприятий, многовариантны. Так как не все варианты одинаково хороши, среди множества возможных приходится отыскивать оптимальный. Значительная часть подобных задач на протяжении долгого времени решалась исходя из здравого смысла и опыта. При этом не было никакой уверенности, что найденный вариант является наилучшим. В современных условиях даже не значительные ошибки могут привести к огромным потерям. В связи с этим возникла необходимость привлечения к анализу и синтезу экономических систем оптимизационных экономико-математических методов и ЭВМ, что создает основу для принятия научно обоснованных решений. Такие методы объединяют в одну группу под общим названием «оптимизационные методы анализа и принятия решения в экономике». Чтобы решить экономическую задачу математическими методами, прежде всего необходимо построить адекватную ей математическую модель, т.е. формализовать цель и условия задачи в виде математических функций, уравнений и (или) неравенств. В общем случае математическая модель оптимизационной задачи имеет вид: max (min) : Z = Z(x) (1.1.) при ограничениях где R – отношения равенства, меньше или больше. Если целевая функция (1.1) и функции, входящие в систему ограничений (1.2.), линейны относительно входящих в задачу неизвестных, такая задача называется задачей линейного программирования. Если же целевая функция (1.1.) или система ограничений (1.2.) не линейна, такая задача называется задачей линейного программирования. В основном, на практике, задачи нелинейного программирования путем линеаризации сводятся к задаче линейного программирования. Особый практический интерес среди задач линейного программирования представляют задачи динамического программирования, которые из-за своей многоэтапности нельзя линеаризовать. Поэтому мы рассмотрим только эти два вида оптимизационных моделей, для которых в настоящее время имеется хорошее математическое и программное обеспечение. Модели и методы решения задачи линейного программирования. Среди оптимизационных моделей и методов, используемых в теории экономического анализа, наиболее широкое распространение получили модели линейного программирования, которые решаются с помощью универсального приема –симплексного метода. Для современных ПЭВМ имеется ряд пакетов прикладных программ, которые позволяют решать любые задачи линейного программирования достаточно большой размерности. Одновременно с решением исходной задачи указанные пакеты прикладных программ могут решать двойственную задачу, решение которой позволяет проводить полный экономический анализ результатов решения исходной задачи. Решение задачи линейного программирования на ПЭВМ рассмотрим на примере задачи об оптимальном раскрое материалов. По результатам решения проведем полный экономико-математический анализ с использованием теории двойственности. Пусть имеется 200 кг полотна шириной 86 см и 300 кг - шириной 89 см. Из него необходимо раскроить и сшить мужские куртки 44, 46, 52 и 54 размеров. Они должны быть изготовлены в следующем соотношении к размерам: 44 - 25,38%; 46 27,88%; 52 - 24,54%; 54 - 25,54%. Итого - 100%. Общий расход полотна, а также отходы, получаемые при рас крое полотна, приведены в табл. 1.12 и 1.13. Количество курток, которые выпускало предприятие в течение месяца, показано в табл. 1.14. Необходимо определить насколько рациональным оказался раскрой, а также какие размеры изделий целесообразнее раскраивать из полотна указанной ширины, чтобы сократить отходы.
Решим данную задачу на ПЭВМ с использованием, например, инструментальных средств МВ Excel и сделаем экономический анализ полученного решения. Как правило, решение конкретной задачи на ПЭВМ включает в себя следующие этапы: · составление математической модели; · присвоение элементам модели определенных «имен»; · составление матричной модели с поименованными элементами; · ввод и корректировка исходных данных; · решение задачи на ПЭВМ; · экономический анализ полученного решения. Применительно к нашему примеру на первом этапе вводим условные обозначения, необходимые для решения задачи (Табл. 1.15.). Здесь х1, х2, х3, х4, х5, х6, х7, х8, обозначают соответственно количество изделий (штук) определенного размера, раскроенных из полотна шириной 86 и 89 см. Умножив количество изделий на нормы отхода, получим общую величину отходов производства. Они должны быть минимальны. Тогда целевая функция имеет вид: min: F(x) = 66,27 х1 + 75.5х2 + 78.4х3 + 95.6х4 + + 94.2х5 + 97.49х6 + 105.7х7 + 108.77х8. Задача состоит в
нахождении таких хj (j= 520,27х1 + 553,5х2 + 597,4х3 + 605,4х4 = 200000; 526,42х5 + 553,49х6 + 627,7х7 + 647,77х8 = 300000; х1 + х2 + х3 + х4 + х5 + х6 + х7 + х8 - х9 = 0; х1 + х5 – 0,2538х9 = 0; х2 +х6 – 0,2788х9 = 0; х3 + х7 – 0,2420х9 = 0 х4 + х8 – 0,2254х9 = 0;
Здесь х9 – суммарный выпуск курток. Тогда условия (1.4) и (1.5) означают, что полотна шириной 86 см должно быть израсходовано 200 кг, а полотна шириной 89 см - 300 кг; (1.6) – условие суммарного выпуска изделий; условия (1.7) – (1.10) означают сбалансированность раскроя изделий по соответствующим размерам; (1.11) – условие неотрицательности объемов производства. На втором этапе каждой переменной, ограничениям, целевой функции и вектору ограничений (коэффициенты свободных членов) присваиваются «имена», которые должны включать не более восьми символов. Удобно, чтобы имена были информативными, так как при этом облегчается использование выходных отчетов. Элементы модели и присваиваемые им имена:
На третьем этапе составляем матричную модель с именованными элементами модели (Приложение 2). . На четвертом этапе введем исходные данные в ПЭВМ. При этом ввод осуществляется в соответствии с инструкцией к имеющемуся пакету прикладных программ. При завершении ввода исходной информации возможна ее распечатка для визуального контроля. По результатам контроля производится корректировка исходной информации и переход на режим расчета. Пятый этап. Решение задачи Возможно в двух режимах: решение прямой задачи; решение прямой и двойственной задач. При этом решение можно производить поэтапно, с выдачей промежуточных результатов алгоритма симплекс-метода, по которым можно судить о качественном процессе поиска оптимального решения. По завершении результатов расчета устанавливается режим распечатки (как прямой задачи, так и двойственной). Так, в режиме расчета прямой задачи получим следующее решение, предварительно округлив результаты до целых: ПР 1 = 150; ПР 2 = о; ПР 3 = 204; ПР 4 = о; ПР 5 = 64; ПР 6 = 235; ПР 7 = о; ПР 8 = 190; ПР 9 = 843. Отходы = 75 743; Полотно 1 = 200 000; Полотно 2 300 = 000. Следовательно, необходимо раскроить из полотна шириной 86 см 150 курток 44 размера и 204 куртки 52 размера, а из полотна шириной 89 см - 64 куртки 44 размера, 235 курток 46 размера и 190 курток 54 размера. Общий объем производства составит 843 куртки. Суммарные отходы при таком варианте раскроя составят 75743 г, а ресурсы будут использованы полностью. В режиме решения двойственной задачи получим значения двойственных оценок ресурсов: Полотно 1 = 0,12996 Полотно 2 = 0,16616 Как видим, двойственные оценки объемов ресурсов отличны от нуля, следовательно, они «дефицитны». Их абсолютная величина говорит о том, что увеличение объема ресурса на единицу приводит к качественному изменению целевой функции (1.1) на величину этой оценки. Следовательно, оценки можно считать количественной мерой дефицита ресурсов: чем больше оценка, тем к большему эффекту приводит увеличение объема использования данного ресурса. Одновременно с этим получим двойственные оценки производимой продукции: ПР 1 = о; ПР 2 = 4,70818; ПР 3 = о; ПР 4 = 4; ПР 5 = о; ПР 6 = о; ПР 7 = 0,73815; ПР 8 = о. Здесь двойственные оценки ПР 2, ПР 4, ПР 7 принимают нулевые значения. Абсолютные значения этих оценок говорят о том, что если мы все же будем раскраивать соответствующие изделия, потери от отходов будут только увеличиваться на величину оценки от раскроя одной единицы изделия. Следовательно, раскраивать куртки 46 и 54 размеров из полотна 86 см нецелесообразно, точно так же как и куртки 52 размера - из полотна шириной 89 см. Теперь сопоставим нормативные отходы при традиционном варианте раскроя с отходами при оптимальном варианте (табл. 1.16).
Из таблицы видно, что наиболее рационален раскрой из полотна шириной 86 см изделий 44 и 52 размеров, а из полотна шириной 89 см - 44, 46 и 54 размеров. Такой способ раскроя уменьшает отходы, увеличивает выпуск изделий, прибыль предприятия и его рентабельность. Отметим, что в современных пакетах прикладных программ для решения задач линейного программирования симплекс-методом предусмотрены режимы расчета так называемых интервалов устойчивости, как для ограниченных ресурсов, так и для переменных величин, принимающих ненулевые значения. Экономический смысл этих интервалов состоит в том, что изменение объемов ресурсов и значений переменных в пределах этих интервалов не изменяет структуру оптимального плана. Это позволяет предприятию проводить рациональную политику приобретения дополнительных ресурсов. БАЛАНСОВЫЕ МЕТОДЫ И МОДЕЛИ В АНАЛИЗЕ СВЯЗЕЙ ВНУТРИЗАВОДСКИХ ПОДРАЗДЕЛЕНИЙ И В РАСЧЕТАХ ЗАТРАТ И ЦЕН. Балансовая модель - это система уравнений, характеризующих наличие ресурсов (продуктов) в натуральном или денежном выражении и направления их использования. При этом наличие ресурсов (продуктов) и потребность в них количественно совпадают. В основу решения таких моделей положены методы линейной векторно-матричной алгебры. Поэтому балансовые методы и модели называют матричными методами анализа. Наглядность изображений различных экономических процессов в матричных моделях и элементарные способы разрешения систем уравнений позволяют применять их в различных производственно-хозяйственных ситуациях. Пусть, например, известно, что каждое предприятие наряду с основным производством имеет вспомогательное, включающее в себя ряд цехов. Вспомогательные цехи оказывают услуги друг другу и основному производству. Величина себестоимости работ и услуг каждого вспомогательного цеха складывается из работ (услуг) других вспомогательных цехов. Чтобы определить затраты, связанные с использованием данным цехом работ (услуг) других цехов, надо наряду с объемом предоставленных работ (услуг) знать их себестоимости. Но, в свою очередь, определение этих себестоимостей невозможно без предварительного исчисления себестоимости работ (услуг), которые цехи получили друг от друга. Механизм использования балансового метода покажем на следующем примере. Пусть на предприятии наряду с основным производством имеется четыре вспомогательных цеха - цех сетей и подстанций, цех водоснабжения, автопарк, ремонтно-механический цех. Все они оказывают услуги друг другу (табл. 1.17).
Требуется определить себестоимость работ (услуг), оказываемых основному производству всеми вспомогательными цехами. Из табл. 1.17 видно, что для определения себестоимости услуг необходимо знать совокупные затраты каждого вспомогательного цеха. А их нельзя подсчитать без расчета себестоимости единицы получаемых услуг одного киловатт-часа электроэнергии, кубометра воды, тонно-километра грузоперевозок, нормо-часа ремонтных работ. Данную задачу можно успешно решать, используя балансовые модели и методы. Обозначим через qij количество продукции, работ, услуг j-гo цеха, поступивших в i-й цех; уi - общие затраты подразделений – потребителей (которые в свою очередь являются поставщиками услуг); Qj - общий объем продукции, работ, услуг в натуральных единицах, отпущенных подразделением-поставщиком; pj – собственные затраты (условно-постоянные и переменные) без стоимости услуг внутризаводского характера; xi – себестоимость единицы продукции, работ, услуг. Взаимное предоставление продукции и услуг отразим в табл. 1.18.
На основе таблицы можно получить следующую систему уравнений:
Приведенные соотношения представляют собой систему двух групп неизвестных: себестоимости единицы продукции, работ, услуг и общего размера затрат по каждому структурному подразделению предприятия. Чтобы решить такую систему, приведем ее к стандартному виду, для чего выражение переменных yi подставим в выражение переменных xi. В результате получим:
После соответствующих преобразований полученную систему уравнений можно записать в матричной форме, для чего введем некоторые виды матриц:
.. 0 0 … 0 … Qm Отсюда
Обратимся к задаче и представим исходную информацию в виде матриц:
В результате решения задачи получены следующие значения себестоимости единицы работ, услуг (хi,): х1= 0,019964 руб., х2 = 0,099536 руб., х3 = 0,099837 руб., х4 = 1,999716 руб. Тогда общая сумма затрат по каждому вспомогательному цеху может быть вычислена по формуле:
Подставив в данное уравнение соответствующие значения, получим: у1 = 59295 + 5 000 х 0,099837 + 50 х 1,999716 = 59 894 руб. у2 = 4 118 + 30 000 х 0,019964 + 600 х 0,099937 + 100 х 1,999716 = 4 977 руб. у3 = 24 020 + 4 500 х 0,019964 + 5 000 х 0,99536 + 400 х 1,999716 = 24 960 руб. у4 = 36 785 + 100 000 х 0,019964 + 1 500 х 0,99536 + 1200 х 0,099837 = 39 994 руб. Следовательно, суммарная себестоимость работ (услуг) вспомогательных цехов, оказываемых основному производству, составит:
Следует отметить, что существующие пакеты прикладных программ для решения матричных моделей на современных ПЭВМ позволяют выполнять расчеты баланса производства и распределения работ (услуг) как в целом по предприятию, так и для каждого структурного подразделения в отдельности и предоставлять пользователю выходную информацию в требуемой форме. ЗАКЛЮЧЕНИЕ Из данной курсовой работы мы узнали, что внедрение экономико-математических методов помогает совершенствовать анализ финансового-хозяйственной деятельности. Их применение повышает эффективность экономического анализа за счет расширения факторов, обоснования принимаемых управленческих решений, выбора оптимального варианта использования хозяйственных ресурсов, выявления и мобилизации резервов повышения эффективности производства. Так же в этой курсовой были рассмотрены некоторые экономико-математические методы и приведены примеры их использования. Список используемой литературы: 1. Басовский Л.Е. Теория анализа хозяйственной деятельности. М.: ИНФРА-М, 2001г. 2. Кравченко Леонид Иванович, Осмоловский Валентин Васильевич, Русак Нина Александровна и др. Теория анализа хозяйственной деятельности. Учебник. Минск 2005г. 3. Муравьев А. И. Теория экономического анализа. М.: Финансы и статистика, 1988г. 4. Савицкая Г. В. Экономический анализ. М.: Новое издание, 2004г. 5. Шеремет А. Д. Теория экономического анализа. М.: ИНФРА-М, 2002г. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Уравнение прямой линии описывает такую связь между
двумя признаками, при которой с изменением признака-фактора происходит
равномерное возрастание или убывание значений зависимого признака (рис. 1.1.)
Уравнение прямой линии описывает такую связь между
двумя признаками, при которой с изменением признака-фактора происходит
равномерное возрастание или убывание значений зависимого признака (рис. 1.1.)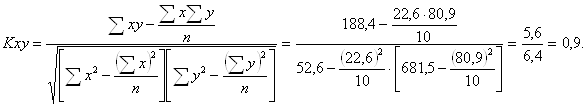 Коэффициент корреляции по
абсолютной величине может принимать значения в пределах от 0 до 1. Если между
двумя показателями не существует связи, коэффициент равен 0, если связь тесная,
- он близок к 1.
Коэффициент корреляции по
абсолютной величине может принимать значения в пределах от 0 до 1. Если между
двумя показателями не существует связи, коэффициент равен 0, если связь тесная,
- он близок к 1.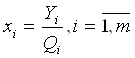 ;
;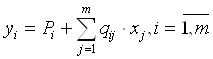 .
. ;
;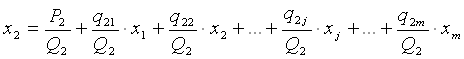 ;
;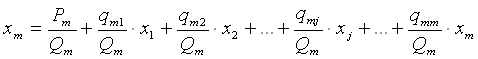 .
.


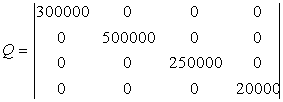
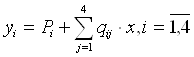
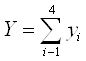 = 59 834 + 4 977 + 24960 + 39 994 = 129825 руб.
= 59 834 + 4 977 + 24960 + 39 994 = 129825 руб.