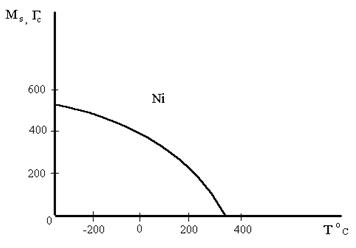
Дипломная работа: Исследование методов наблюдения доменов в тонких ферромагнитных пленках

Температурная зависимость плотности спонтанного магнитного момента М (Т) никеля показана на рисунке 12 [5, с. 99].

Рисунок 12 - Зависимость спонтанного магнитного момента Ni от температуры.

В учении о магнитоупорядоченных веществах важную роль играют представления о магнитных фазовых переходах. Различают магнитные переходы 1-го и 2-го рода. Переходы 1-го рода характеризуются непрерывным изменением термодинамических функций, например свободной энергии, или термодинамического потенциала системы Ф (Т, Р, Н), где Т, Р, и Н – внешние термодинамические параметры, но испытывают скачок первые производные Ф´ (Т, Р, Н). Поскольку

(Ф/Т)Р, Н = Q

и

(Ф/Н)Т, Р = I,

то при переходе первого рода существуют скачки скрытой теплоты Q и намагниченности I.

Переходы 2-го рода характеризуются непрерывным изменением функций Ф (Т, Р, Н) и Ф´ (Т, Р, Н), однако скачки испытывают вторые производные Ф´´ (Т, Р, Н); это означает, что существуют скачки в точке перехода 2-го рода теплоемкости (Q/T)Р, Н = CР, Н и температурного коэффициента намагниченности (I/h)Т, Р. Рассматриваемые переходы являются магнитными переходами типа порядок – беспорядок (например, ферромагнетизм – парамагнетизм). На рисунке 13, б показано схематическое изменение самопроизвольной намагниченности I, при магнитных переходах 2-го рода типа порядок – беспорядок. В большинстве магнитоупорядоченных веществ в точках Кюри и Нееля возникают именно такие переходы.

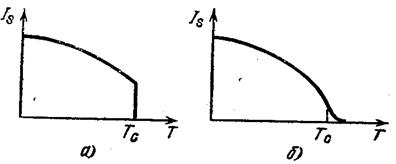
Рисунок 13 - Магнитные фазовые переходы 1-го (а) и 2-го (б) рода.

Согласно Ландау магнитный переход 2-го рода можно приближенно описать с помощью разложения энергии ферромагнетика в ряд по четным степеням параметра магнитного упорядочения, за который можно принять намагниченность I.Для случая ферромагнетика имеем

W = W0 + aI2 + bI4 – IH (15)

где W0 – аддитивная постоянная,

а и b – некоторые коэффициенты (знак минус перед энергией поля IH означает, что магнитная система находится в стабильном состоянии). Из условия равновесия магнитной системы W/I = 0 получаем уравнение состояния ферромагнетика вблизи точки Кюри Тс.

αI + βI3 = H (16)

где α = 2а, β = 4b – новые коэффициенты, зависящие от Т и Р; в частности, можно коэффициент α разложить в ряд по разности Т – Т:

α =αТс (Т – Т ) (17)

В отсутствии магнитного поля I = Is. Из (16) и (17) имеем

I = - (αТc / β) (Т –Т) (18)

При достижении температуры Т = Т намагниченность Is = 0 и, следовательно, α = 0. Таким образом, равенство α = 0 может быть использовано для определения температуры Кюри. Последнее уравнение можно записать в виде:

Is = A (Т –Т)1/2 (19)

где

А = (αТс /b)1/2

При Т = Т, т.е. a = 0, из (16) имеем:

I = ВН 1/3 (20)

где В = (1/b)1/3. Присоединяя сюда соотношение

χ = С (Т – Т)-1 (21)

(закон Кюри – Вейсса, который справедлив при Т ≥ Т), мы получаем три уравнения для описания магнитного перехода в окрестности точки Кюри.

Однако эти уравнения весьма приближенны, особенно в узкой окрестности точки Кюри, т.е. в области |τ| =(Т – Т) / Т ≤ 10-4. В этой области возникают так называемые флуктуации магнитного порядка – критическое состояние вещества. Влияние этих флуктуаций в самой точке Т приводит к корреляции спинов, что должно быть учтено с помощью введения новых показателей, степеней в систему уравнений (19) – (21), а именно:

I = A (Т –Т)b, I = ВН 1/d, χ =С(Т –Т) (22)

где b, d и g - так называемые критические индексы магнитного перехода. Все термодинамические функции вблизи перехода испытывают резкие изменения (сингулярности), и поэтому эти индексы должны быть более высокими, чем дает термодинамика Ландау.

Априори можно утверждать, что между критическими индексами должна существовать количественная связь, так как все процессы, протекающие в критической области, взаимосвязаны. Оказывается, связь между ними довольно проста (закон подобия):

g = b (d - 1) (23)

Измерениями для Ni и некоторых ферритов установлено, что g = 1,3; b = 0,38; d = 4,42. Подставляя эти значения в закон подобия, можно убедиться, что этот закон удовлетворяется.

Отметим, что уравнение I = ВН 1/d является аналогом уравнения состояния жидкости:

r - rкр = а (Р – Ркр)1/d

где r - плотность, Р – давление; вблизи точки перехода (критической точки) r = rкр, Р = Ркр. Измерения показали, что вблизи критической точки (Т = Ткр) критический индекс d для системы жидкость – газ равен 4,2; т.е. приблизительно такой, как и для системы ферромагнетик – парамагнетик. Из этого следует, что результаты по изучению механизма фазовых переходов в магнитных веществах можно переносить на более сложные переходы, происходящие в твердых и жидких телах. Поэтому физики проявляют такой большой интерес к исследованию магнитных фазовых переходов.

Исследованиями установлено, что в небольшом числе магнитоупорядоченных веществ в точке Кюри происходит переход 1-го рода. В этом случае температурный ход самопроизвольной намагниченности, в отличие от перехода 2-го рода, при приближении к T обрывается скачком (рисунок 13, а). Такой переход был обнаружен в сплаве MnAs и некоторых других.

Помимо переходов типа порядок – беспорядок в магнитоупорядоченных веществах могут быть магнитные переходы типа порядок – порядок (например, ферромагнетизм – антиферромагнетизм). Эти переходы могут возникать самопроизвольно при достижении определенной критической температуры или под действием внешнего магнитного поля при достижении критического поля. В зависимости от «резкости» перехода они могут быть переходами 1-го или 2-го рода.

Для веществ, обладающих такими переходами, строят так называемые магнитные фазовые диаграммы. При достижении определенной температуры и магнитного поля в веществе может проявляться магнитная тройная точка (трикритическая точка) Т., в которой сосуществуют три состояния вещества: антиферромагнитное, метамагнитное (неустойчивое ферромагнитное состояние) и парамагнитное. Выше тройной точки в магнитном поле при повышении Т наблюдаются переходы: антиферромагнетизм – метамагнетизм - парамагнетизм.

В последние годы исследованы так называемые магнитоориентационные переходы, при которых скачком или плавно (переходы 1-го или 2-го рода) изменяется направление вектора самопроизвольной намагниченности Is по отношению к осям кристалла. Эти переходы особенно распространены в редкоземельных магнитоупорядоченных веществах [1, с.52-55].

1.8 Ферромагнетизм и кристаллическая решетка

Измерение магнитных моментов атомов ферромагнитных элементов показало, что они по порядку величины такие же как у атомов парамагнитных элементов, т.е. составляют несколько магнетонов Бора. Но даже в очень сильных магнитных полях намагниченность парамагнетиков проявляется очень слабо, а ферромагнетики приобретают высокую степень намагниченности и в сравнительно слабых внешних магнитных полях. В чем же причина столь необычных свойств ферромагнетиков?

Спиновая природа ферромагнетизма, обнаруженная гиромагнитными опытами, позволяет высказать предположение, что необходимым условия существования ферромагнетизма является наличие в атомах ферромагнетиков нескомпенсированных спиновых магнитных моментов электронов.

Действительно, у всех ферромагнитных элементов в недостроенной оболочке имеются нескомпенсированные спины электронов (у железа, например, 4 нескомпенсированных спина, у кобальта - 3, у никеля – 2).

Но это необходимое условие – наличие нескомпенсированных спинов в недостроенных оболочках атома – еще не достаточно для возникновения ферромагнетизма. У марганца имеются 5 нескомпенсированных спинов, у хрома – 4, но оба они не ферромагнитны.

Заметив, что ферромагнетизм проявляется только у кристаллических тел, будем причину его искать в кристаллическом строении ферромагнетиков.

Оказывается, что возможность ферромагнетизма определяется таким правилом: отношение параметра кристаллической решетки к диаметру электронной орбиты, на которой находится электрон с нескомпенсированным спином, должно быть больше 1,5, т.е.

a/ 2R > 1,5 (24)

где a - параметр решетки;

R – радиус орбиты электрона с нескомпенсированным спином.

Для хрома и марганца правило (24) не выполняется, поэтому они не ферромагнитны. Но некоторые сплавы внедрения на основе марганца и хрома являются ферромагнитными. Это относится к сплавам, у которых параметр решетки d увеличен (из-за внедрения в решетку атомов второй компоненты сплава) до величины, соответствующей условию (24). То же самое можно сказать про ферромагнитный сплав Гейслера (Сu2MnAl), состоящий из неферромагнитных металлов. Сплав Гейслера является ферромагнитным вследствие сочетания двух обстоятельств:

в него входит элемент (марганец), имеющий в недостроенной М-оболочке нескомпенсированные спины;

параметр кристаллической решетки сплава и диаметр орбиты электронов с нескомпенсированным спином таковы, что удовлетворяют неравенству (24).

Таким образом, кристаллическое строение вещества является одним из определяющих факторов принадлежности или непринадлежности данного вещества к категории ферромагнетиков [3, с. 202-203].

1.9 Гистерезисные явления в ферромагнетиках

Представим себе, что мы взяли ненамагниченный кусок железа и поместили его в плавно возрастающее магнитное поле. Тогда, очевидно, железо начнет плавно намагничиваться, намагниченность его будет расти, пока при достаточно сильном поле Н, не достигнет своего насыщения.

Процесс намагничивания образца, ранее не помещавшегося в магнитное поле, представлен на рисунке 14 кривой Оа. Если теперь уменьшать напряженность магнитного поля, то будет уменьшаться и намагниченность. Однако при определенных значениях магнитного поля мы уже не получим тех значений намагниченности, которые соответствовали этим полям при нарастании поля. Другими словами, кривые намагничивания образца, соответствующие возрастанию и уменьшению поля, не совпадают.

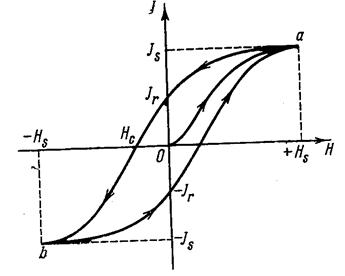
Рисунок 14 - Петля гистерезиса ферромагнетика.

Как показывает опыт, кривая, соответствующая уменьшению поля, пойдет выше. Это явление отставания спада намагниченности от спада поля носит название магнитного гистерезиса.

В поле, равном нулю на кривой размагничивания, намагниченность не обращается в нуль, а имеет некоторое значение Jr, которое носит название остаточной намагниченности. Чтобы свести эту остаточную намагниченность к нулю, нужно приложить поле Нс, направленное противоположно.

Поле Нс, при котором остаточная намагниченность обращается в нуль, носит название коэрцитивного (задерживающего) поля или коэрцитивной силы.

Если продолжать увеличивать поле противоположного направления (отрицательное поле), то при полях, превышающих значение коэрцитивной силы, образец начнет намагничиваться в направлении, противоположном начальному. Эта отрицательная намагниченность с ростом поля будет расти и достигнет насыщения, численно равного величине насыщения при положительной намагниченности.

Уменьшая отрицательное поле, мы получим такую же картину, как и в случае размагничивания от насыщения при положительном поле, т.е. когда поле обратится в нуль, то отрицательная намагниченность в нуль не обратится, а будет равна -Jr. Чтобы свести эту отрицательную намагниченность к нулю, следует приложить положительное магнитное поле, равное коэрцитивному полю. Увеличивая положительное значение поля, мы получим положительную намагниченность, которая будет расти вместе с полем, пока не достигнет насыщения.

Таким образом, при изменении величины поля от максимального положительного до максимального отрицательного значения и обратно кривая, характеризующая намагниченность, образует петлю, которая называется петлей гистерезиса. Если мы снова повторим цикл, изменяя поле от +Нs до –Нs и обратно, то мы опишем ту же самую петлю. По такой петле мы будем «ходить» при многократном перемагничивании. Что касается кривой Оа, то ее можно получить снова только при условии предварительного полного размагничивания образца. Поэтому эта кривая носит название первообразной или первичной кривой.

Размагнитить образец можно, например, при помощи многократного переключения тока (коммутации) в катушке, при одновременном уменьшении его величины от значений, соответствующих магнитному насыщению образца, до нуля.

Вследствие магнитного гистерезиса при одном и том же значении магнитного поля намагниченность образца может иметь различные значения, которые зависят не только от напряженности магнитного поля, но и от предыстории образца.

Такая петля гистерезиса, при которой намагниченность изменяется от +Js до –Js, носит название предельной.

Она является одной из важных характеристик ферромагнетика. Материалы с большой коэрцитивной силой имеют широкую петлю гистерезиса. Они трудно размагничиваются и называются магнитно-жесткими материалами. Из таких материалов изготавливают постоянные магниты.

Магнитно-мягкие материалы, наоборот, обладают малой коэрцитивной силой и узкой петлей гистерезиса. Такие материалы используются в трансформаторах, статорах и роторах динамомашин и т.д.

В табл. 4 приводятся данные о коэрцитивных силах Нс и максимальной магнитной проницаемости mмакс некоторых магнитных материалов.

Таблица 4. Характеристика некоторых магнитных материалов

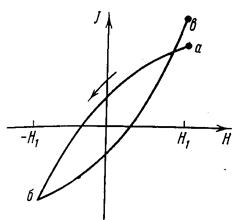
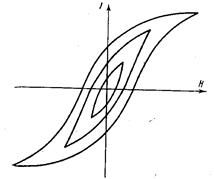
* В таблице приведены весовые проценты

Если циклическое перемагничивание осуществляется при максимальном значении поля, меньшем поля насыщения, то гистерезисные явления протекают еще более сложно.

Пусть при напряжении поля Н1 намагниченность ферромагнитного образца соответствует точке а на рисунке 15. Поскольку поле меньше поля насыщения, то и намагниченность J будет меньше Js.

Если теперь плавно уменьшить поле до –Н1, то намагниченность будет изменяться по кривой аб, и при повторном возрастании поля до Н1, намагниченность, как правило, не совпадает с точкой а, а будет иметь несколько большее значение, изображенное на рисунке точкой в. Полученная незамкнутая петля носит название неустановившейся петли гистерезиса.

При повторных циклах картина будет повторяться, но при одинаковых значениях поля расхождения в значениях намагниченности будет все меньше и, наконец, при многократном циклическом изменении поля намагниченность будет описывать замкнутую кривую, которая называется симметричной петлей гистерезиса. На рисунке16 представлено семейство симметричных петель гистерезиса, соответствующих различным значениям поля. Как видно из рисунка, предельная петля гистерезиса является симметричной петлей, соответствующей значениям намагниченности насыщения.

Рисунок 15 - Неустановившаяся петля гистерезиса.

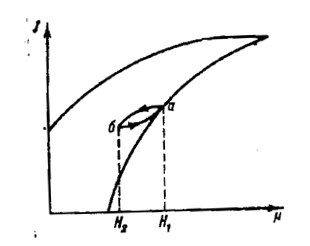
Рисунок 16 - Семейство симметричных петель гистерезиса.

Для получения симметричной петли обычно достаточно провести около десяти перемагничивающих циклов. Если поле периодически меняется не относительно своего нулевого значения, а от Н1 до Н2 и обратно (рисунок 17), то намагниченность описывает замкнутую кривую аба, называемую частным гистерезисным циклом.

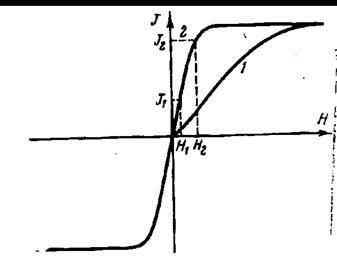
Рисунок 17 - Частный гистерезисный цикл.

Гистерезисные явления свидетельствуют о наличии необратимых процессов, которые протекают в ферромагнетике при наложении на него изменяющегося магнитного поля. Ферромагнетик, как правило, находится при этом не в равновесном состоянии, соответствующем минимуму свободной энергии при данной напряженности магнитного поля и температуре. Однако есть ряд приемов, позволяющих снять кривые намагничивания, которые при циклическом изменении поля не дают гистерезисной петли. Такие кривые носят название безгистерезисных или идеальных кривых намагничивания и соответствуют минимуму свободной энергии.

На рисунке 18 показана обычная (первичная) кривая намагничивания (кривая 1) и идеальная безгистерезисная кривая (кривая 2). Продолженная в область отрицательных полей идеальная кривая при циклическом изменении поля не дает петли. Безгистерезисная кривая может быть получена различным образом. Наиболее распространенный способ заключается в следующем. На ферромагнитый образец накладывается некоторое небольшое постоянное магнитное поле Н1 и переменное поле низкой частоты, амплитуда которого превышает поле насыщения, затем амплитуду переменного поля медленно сводят к нулю, фиксируя при этом значение намагниченности J1.

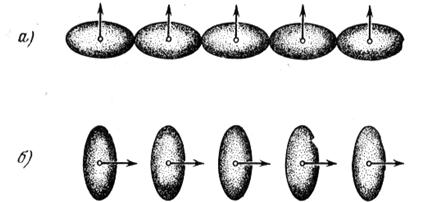
Рисунок 18 - Первичная (1) и идеальная (2) кривые намагничевания.

Безгистерезисную кривую намагничивания можно получить еще и таким образом. На ферромагнитный образец накладывается магнитное поле Н1, после чего ферромагнетик нагревается до температуры выше точки Кюри и медленно охлаждается до исходной температуры; значение намагниченности J1 фиксируется. Затем поле увеличивается до некоторого значения Н2, образец вновь нагревается выше точки Кюри, охлаждается до исходной температуры и вновь измеряется намагниченность J2 и т.д.

Совокупность точек, соответствующих намагниченностям J1, J2 и т.д. (при намагничивающих полях Н1, Н2 и т.д.), дает безгистерезисную кривую намагниченности. Иногда удается получить безгистерезисную кривую наложением периодических напряжений. Следует отметить, что идеальная кривая, снята вторым способом – методом «температурной тряски», всегда идет выше безгистерезисной кривой, полученной другими способами [7, с.50-55].

1.10 Магнитная анизотропия

В ферромагнитном кристалле имеются взаимодействия, которые ориентируют вектор намагниченности вдоль определенных кристаллографических направлений, называемых осями легкого намагничивания.

Энергия, связанная с этими взаимодействиями, называется энергией магнитной кристаллографической анизотропии или просто энергией магнитной анизотропии.

Одна из причин магнитной анизотропии иллюстрируется схемой на рисунке 19. Намагниченность кристалла «чувствует» кристаллическую решетку благодаря перекрытию электронных орбит: спиновые моменты взаимодействуют с орбитальными из-за наличия спин-орбитальной связи, а орбитальные моменты в свою очередь взаимодействуют с кристаллической решеткой за счет существующих в ней электростатических полей и перекрытия волновых функций соседних атомов решетки [8, с. 581-582].

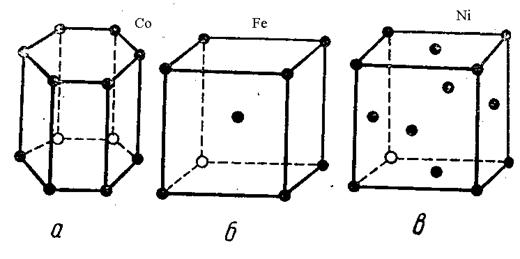
Рисунок 19.

Все известные в настоящее время ферромагнетики – тела кристаллические. Кристаллики очень малы. Но если хорошо отполированную поверхность протравить кислотой и исследовать под микроскопом, то мы увидим различные по форме и величине зерна. Тщательное изучение показывает, что эти отдельные зерна представляют собой кристаллы с неправильными поверхностными границами.

Неправильность границ объясняется тем, что при кристаллизации вещества одновременно начинает расти большое количество кристаллов и они мешают друг другу принять правильные граничные очертания.

Кристаллы, граничная поверхность которых не представляет собой правильной, характерной для кристаллов формы, называются кристаллитами. В кристаллических телах атомы расположены в строго определенном порядке и составляют так называемую кристаллическую решетку. Кристаллические решетки могут быть разнообразными (примеры на рисунке 20).

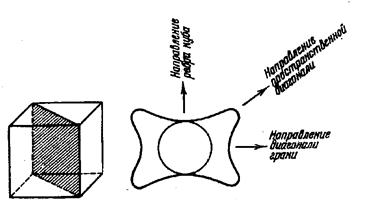
Рисунок 20 - Элементарные ячейки кристаллических решёток: а) гексагональная; б) объёмноцентрированная; в) гранецентрированная.

Асимметрия перекрытия электронных оболочек соседних ионов как одна причин кристаллографической магнитной анизотропии. Вследствие спин-орбитального взаимодействия распределение электронного заряда – не сферическое. Асимметрия связана с направлением спина, поскольку изменение направления спина по отношению к осям кристалла изменяет обменную энергию, а также электростатическую энергию взаимодействия распределений заряда пар атомов. Именно эти эффекты приводят к появлению энергии анизотропии. Энергия системы а иная, чем энергия системы б.

Для кристаллов характерна анизотропность физических свойств. Это значит, что в кристаллах по различным направлениям свойства различны. В телах же не кристаллических (аморфных) все физические свойства по различным направлениям совершенно одинаковы.

Поскольку все ферромагнетики – тела кристаллические, а последним свойственна анизотропия различных физических свойств, то возникает вопрос: являются ли магнитные свойства ферромагнетиков изотропными или анизотропными, т.е. существует ли анизотропия магнитный свойств и если существует, то каких именно?

1) Естественно прежде всего выяснить, как зависит величина спонтанной намагниченности от ее направления в кристалле. Нам уже известно, что величина спонтанной намагниченности равна намагниченности насыщения. Значит, измеряя в кристалле намагниченность насыщения по разным направлениям, мы будем получать значения спонтанной намагниченности по этим направлениям.

Оказалось, что величина спонтанной намагниченности по всем направлениям в кристалле совершенно одинакова. Это справедливо для всех ферромагнитных кристаллов. Для всех ферромагнитных кристаллов характерна изотропия спонтанной намагниченности.

2) Можно исследовать зависимость точки Кюри от направления намагниченности в кристалле, т.е. установить, по всем ли направлениям в кристалле при одной и той же температуре исчезают ферромагнитные свойства.

Оказывается, что и точка Кюри ферромагнетика для всех направлений в кристалле совершенно одинакова. Ферромагнитные свойства теряются в ферромагнетике по всем направлениям при одной и той же температуре. Изотропность точки Кюри объясняется изотропностью спонтанной намагниченности.

Если снимать кривые намагничивания по различным направлениям в ферромагнитных кристаллах (например, для железа), то скажется следующее. Намагниченность монокристалла железа в направлении ребра –куба резко возрастает уже в слабых полях и быстро достигает насыщения (рисунок 21).

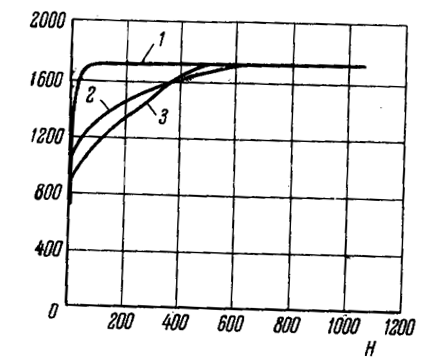
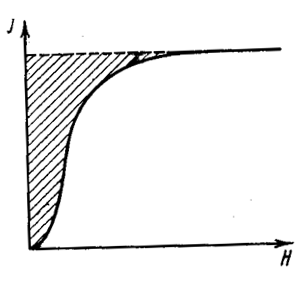
вдоль ребра куба (направление [100])

вдоль диагонали грани (направление [110])

вдоль пространственной диагонали (направление [111]).

Рисунок 21 - Кривые намагничивания монокристалла железа по различным кристаллографическим направлениям

При намагничивании вдоль диагонали грани кривая намагничивания сначала резко идет вверх, как и при намагничивании в направлении ребра куба, затем при достижении приблизительно 0,7 от величины насыщения рост намагниченности замедляется и на кривой намагничивания появляется излом. При дальнейшем возрастании поля намагниченность увеличивается. Насыщение намагниченности наблюдается в довольно сильных полях, причем ее величина равна насыщению, полученному при намагничивании вдоль ребра куба (см. рисунок 21, кривая 2). На том же рисунке видно, что при намагничивании вдоль пространственной диагонали быстрый рост намагниченности прекращается, когда она достигает примерно 0,58 от насыщения. Кривая намагничивания в этом месте претерпевает излом, затем следует медленное возрастание намагниченности с ростом поля, пока не будет достигнуто насыщение (кривая 3, рисунок 21).

Таким образом, намагничивание монокристалла железа по различным направлениям происходит по-разному, т.е. в ферромагнитных кристаллах существует магнитная анизотропия.

Магнитную анизотропию удобнее всего характеризовать работой намагничивания. В самом деле, при намагничивании ферромагнетика расходуется некоторое количество энергии, численно определяемое площадью, ограниченной осью намагниченности, кривой намагничивания и продолжением прямой, соответствующей насыщению, до пересечения с осью намагниченности (рисунок 22).

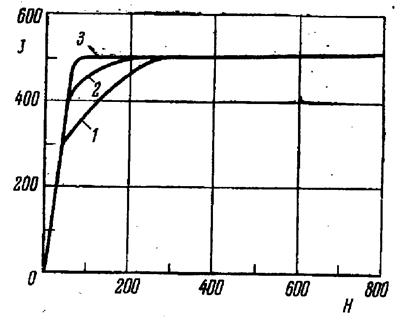
Рисунок 22. Заштрихованная площадь численно равна работе намагничивания.

Из рисунка 21 следует, что работа намагничивания вдоль направления ребра куба для железа наименьшая, вдоль пространственной диагонали – наибольшая, а при намагничивании вдоль диагонали грани она имеет некоторое среднее значение.

Поэтому направление вдоль ребра куба в железе называют направлением легкого намагничивания, а направление, совпадающее с направлением пространственной диагонали, направлением трудного намагничивания.

Исследования, проведенные на монокристаллах никеля, дают прямо противоположную картину. Здесь наибольшая работа при намагничивании затрачивается вдоль ребра куба, которое является направлением трудного намагничивания (рисунок 23, кривая 1). Направлением легкого намагничивания является направление пространственной диагонали  (рисунок 23, кривая 3). На рисунке 2 кривая 2 соответствует намагничиванию монокристалла никеля по диагонали грани.

1-вдоль ребра куба;

2-вдоль диагонали грани;

3-вдоль пространственной диагонали.

Рисунок 23 - Кривые намагничевания монокристалла никеля вдоль различных кристаллографических направлений

Монокристалл кобальта имеет всего одну ось легкого намагничивания, совпадающую с направлением гексагональной оси (рисунок 24). На рисунке 25 изображены кривые намагничивания монокристалла кобальта в направлении гексагональной оси (1) и перпендикулярно к ней (2). Таким образом, в железе имеются три оси (6 направлений по оси и против нее) легкого намагничивания и 4 оси (8 направлений) трудного намагничивания; в никеле – 4 оси (8 направлений) легкого намагничивания, 3 оси (6 направлений) трудного намагничивания; в кобальте – 1 ось (2 направления) легкого намагничивания и бесконечное число направлений трудного намагничивания, перпендикулярных гексагональной оси.

.

Рисунок 24. Направление лёгкого намагничивания в монокристалле кобальта совпадает с гексагональной осью.

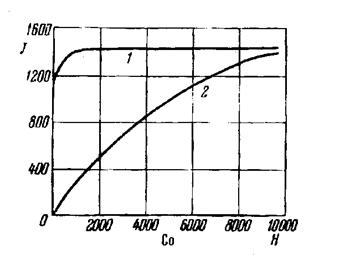
Согласно закону сохранения энергии, работа, затраченная на намагничивание ферромагнетика, не может исчезнуть, она превращается в потенциальную энергию намагниченного тела.

Всякое тело, предоставленное самому себе, стремится занять положение, соответствующее минимуму его потенциальной энергии. В соответствии с этим принципом железный стержень в магнитном поле своей осью установится вдоль поля, так как намагничивание вдоль оси стержня требует меньшей энергии, чем намагничивание поперек стержня.

Вырежем шар из монокристалла железа или никеля и поместим его в магнитное поле, предоставив ему возможность любым образом ориентироваться в пространстве. Последнее можно осуществить, например, при помощи подвеса Кардана (рисунок 26).

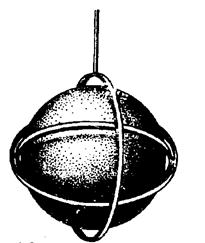
Рисунок 26 - Шар в подвесе Кардана.

Так как работа намагничивания по различным направлениям в кристалле различна, то шар будет вести себя в магнитном поле, как магнитная стрелка, устанавливаясь вдоль поля одной из своих осей легкого намагничивания. На рисунке 27 изображен шар из монокристалла никеля, на котором точками отмечены выходы осей легкого намагничивания. Таких осей четыре.

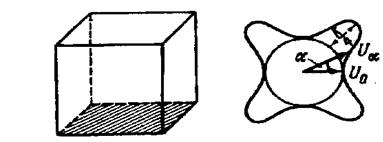
Рисунок 27 - Шар из монокристалла никеля. Точками отмечены выходы на поверхность осей лёгкого намагничивания.

Представим себе теперь, что мы ориентировали шар из монокристалла железа в направлении грани куба по отношению к полю. Кристалл намагнитится, и так как намагничивание происходит в направление оси легкого намагничивания, работа намагничивания будет минимальной.

Если теперь поворачивать этот кристалл в магнитном поле, то намагничивание уже не будет совпадать с направлением легкого намагничивания в кристалле, и работа намагничивания будет возрастать. Представим себе, что кристалл ориентирован так, что вектор напряженности магнитного поля лежит в кристаллической решетке в плоскости грани куба. Тогда с изменением угла поворота кристалла относительно поля работа намагничивания будет периодически то возрастать, то уменьшаться.

Пусть работа намагничивания в направлении ребра куба равна U0. Изобразим эту величину в виде отрезка, который численно равен U0. При повороте кристалла на некоторый угол a величина энергии изменится. Пусть она будет равна Ua. Отложим под углом a к отрезку, изображающему U0, отрезок, равный Ua. Если определить значения Ua для различных углов и откладывать под этими углами отрезки, равные значениям энергии, затрачиваемой при намагничивании шара под соответствующим углом, то получим график энергии намагничивания по различным направлениям в плоскости грани куба, или, как говорят, энергетическую диаграмму в этой плоскости (рисунок 28). Как уже отмечалось, различные значения работы намагничивания по различным направлениям в кристалле и характеризуют собой магнитную анизотропию. Численно магнитная анизотропия равна учетверенной разности работ намагничивания в направлении ребра куба и в направлении диагонали грани (рисунок 28).

Рисунок 28 - Энергетическая диаграмма в плоскости грани куба монокристалла железа.

Эта величина, отнесенная к единице объема, представляет собой важную характеристику ферромагнетика и называется константой магнитной анизотропии.

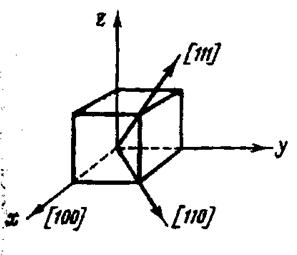
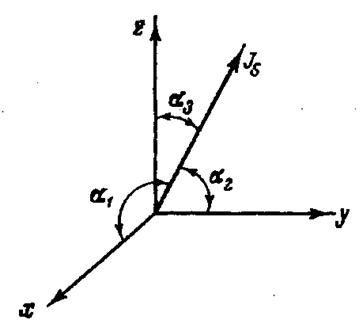
Рисунок 29 - Энергетическая диаграмма монокристалла железа для диагональной плоскости.

На рисунке 29 представлена энергетическая диаграмма в диагональной плоскости кубической решетки. Как видно из рисунка, «горб» соответствует направлению трудного намагничивания, а наиболее глубокие лунки соответствуют направлениям легкого намагничивания.

Изучение энергетической анизотропии кристаллов позволило Н.С. Акулову рассчитать кривые намагничивания монокристаллов по различным направлениям. Рассчитанные кривые оказались в хорошем согласии с опытом.

Для кристаллов кубической системы, энергия, связанная с анизотропией:

U = U0 + K (s12s22 + s22s32 + s12s32 ) (25)

где U0 – энергия в направлении ребра куба кристалла, которое обозначают [100] (рисунок 30);

s1, s2, s3 – косинусы углов между направлениями X, Y, Z и вектором спонтанной намагниченности Js (рисунок 31). При комнатной температуре константа магнитной анизотропии К для железа равна +4,28·105 эрг/см3, а для никеля – 5,12·104 эрг/см3.

Рисунок 30 - Главные кристаллографические направления в кубическом кристалле.

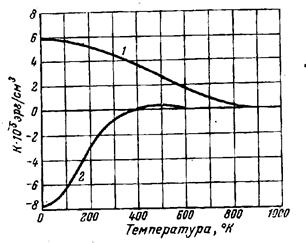
Рисунок 31. S=cos ; S=cos ; S=cos ;

Константа магнитной анизотропии меняется с изменением температуры. На рисунке 32 представлены графики зависимости констант магнитной анизотропии железа и никеля от температуры. Обращает на себя внимание резкая зависимость от температуры константы анизотропии никеля. Даже в области комнатных температур ее величина изменяется в полтора раза.

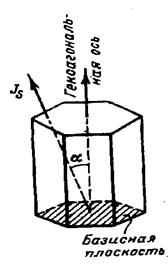
Рисунок 32 - Температурная зависимость констант магнитной анизотропии 1- для железа; 2- для никеля;

Энергия анизотропии для гексагональных кристаллов типа кобальта выражается формулой:

U = U0 + K1 sin2a + K2 sin4a (26)

где К1 и К2 – первая и вторая константы анизотропии;

a - угол между гексагональной осью и направлением вектора спонтанной намагниченности (рисунок 33).[7, с. 65-74]

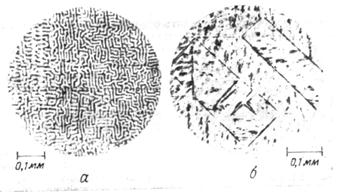
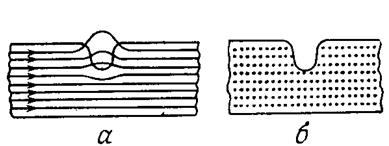
Рисунок 33.

1.11 История обнаружения доменов

У обычных ферромагнитных образцов вследствие их конечных размеров энергетически более выгодным оказывается разделение кристалла на ряд антипараллельно намагниченных областей – доменов. Чем на большее количество таких доменов разобьется образец, тем меньше будет его магнитная энергия. Таким образом, в целом ферромагнетик оказывается разделенным на множество доменов, намагниченных до насыщения так, что результирующая намагниченность образца в отсутствие внешнего поля равна нулю.

Впервые предположение о существовании магнитных доменов для объяснения быстрого намагничивания ферромагнетиков в сравнительно слабых магнитных полях высказал в 1892 году русский учетный Б.Л. Розинг, а затем в 1907 году – французский ученый П. Вейсс [2, с. 99]. В 1907 году Вейсс ввел понятие спонтанной намагниченности и дал теоретическое объяснение того факта, что, несмотря на наличие у ферромагнетиков спонтанной намагниченности, сильно намагнитить их удается не всегда. Он предположил, что ферромагнетик развит на множество магнитных доменов, причем направление спонтанной намагниченности меняется от домена к домену [9, с.154].

Реальность существования областей спонтанной намагниченности доменов была подтверждена двумя фактами. Первый заключается в скачкообразном изменении намагниченности ферромагнетика при плавном увеличении внешнего магнитного поля. Было установлено, что изменение магнитного момента при одном скачке связано с перемагничением внешним полем некоторого числа доменов с одинаковым направлением намагниченности, т.е. определенного объема ферромагнетика. Обычно на кривой намагничения эти скачки незаметны, что объясняется малой величиной скачка и большим их количеством. Скачки становятся заметными при увеличении обычного масштаба кривой намагничения приблизительно в 109 раз. Этот эффект впервые был обнаружен в 1919 году Баркгаузеном и назван его именем.

Вторым фактором, доказавшим реальность доменов, было получение на отполированной поверхности ферромагнетика характерных узоров – фигур Акулова-Биттера [2, с. 99]. Попытки увидеть магнитные домены непосредственно в микроскоп были впервые предприняты в 1932 году Биттером и независимо от него Хамосом и Тиссеном.

В этих экспериментах исследователи наносили на ферромагнитный кристалл суспензию, содержавшую мелкие ферромагнитные взвешенные частицы, а затем старались рассмотреть в металлографический микроскоп образуемое ими изображение магнитных доменов. В результате была получена великолепная картина магнитных доменов, хотя Биттер и не решился делать выводы об их форме, а в заглавии статьи говорилось просто о неоднородностях в ферромагнетиках. Возможно, так произошло потому, что, принимая общепризнанное в то время мнение о размерах доменов, сформировавшееся после обнаружения эффекта Баркгаузена, Биттер был убежден, что магнитные домены не могут быть столь большими, какими они были на фотографиях. Вскоре было выполнено множество наблюдений доменов, но в то время не принимали в расчет магнитостатическую энергию и потому не заботились о том, чтобы кристаллы были вырезаны строго параллельно плоскостям, в которых лежит намагниченность, поэтому изображения не были четкими.

Тогда же крупный вклад в развитие метода суспензии и метода электрополировки внес изучавший домены Элмор. Созданная им техника была использована затем в работах группы Уильямса, что и принесло успех этим исследователям. В то же время магнитологов ввела в заблуждение обнаруженная лабиринтная структура (рисунок 34, а). Речь идет об изображениях мельчайших магнитных доменов с размерами 0,01 мм. и ниже.

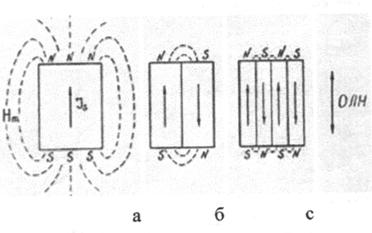
Рисунок 34 - Магнитные домены, наблюдавшиеся методом порошковых фигур на монокристалле железа в плоскости (001): а – лабиринтная доменная структура поверхностного слоя; б – магнитные домены, появившиеся после удаления электрополировкой деформированного поверхностного слоя глубиной 28 мкм.

Если вычислить объем этих доменов, получится значение, примерно совпадающее с величиной 10-8 см3, найденной из эффекта Баркгаузена. В результате ошибочной интерпретации полученного результата сложилось мнение, что домены малы. Однако Кая в работе 1934 г. доказал, что появление лабиринтной структуры обусловлено поверхностной деформацией, возникающей при шлифовке кристаллической поверхности; выяснилось также, что эти изображения не отражают действительной формы магнитных доменов, и проблема, связанная с размерами магнитных доменов, по-прежнему осталась неразрешенной.

В 1935 г. Ландау и Лифшиц дали чисто теоретическое объяснение доменной структуры и правильно предсказали форму доменов, что позволило навести порядок в хаосе экспериментальных результатов. Затем в 1944 г. Неель выполнил расчеты мелкой доменной структуры, причем впервые учел при этом магнитостатическую энергию. Полученная геометрическая структура доменов весьма заметно расходилась с тогдашними представлениями о ней, но в конце концов в 1949 г. теоретические результаты были полностью подтверждены в замечательных экспериментах с порошковыми фигурами, выполненных Уильямсом, Бозортом и Шокли (лаборатория фирмы «Белл»). На рисунок 34 б, показано изображение доменов, полученное по методу этих авторов после удаления поверхностного деформированного слоя. Как можно убедиться, размеры доменов в данном случае существенно больше, чем в лабиринтной структуре.

Данный метод наблюдения доменов аналогичен способу получения изображения силовых линий магнита, расположенного под листом бумаги, с помощью насыпаемых сверху железных опилок. Он состоит в том, что на отшлифованную поверхность ферромагнетика наносят сверху мельчайшие магнитные частицы и наблюдают в микроскоп доменную структуру. Называется этот способ методом порошковых фигур [9, с.156-157].

1.12 Возникновение доменов

Кристаллы ферромагнетиков состоят из магнитных доменов. Каждый домен – это область, намагниченная до насыщения однородно, т.е. векторы спонтанной намагниченности Js, построеные в различных точках домена, параллельны.

Форма доменов, их размер, взаимное расположение доменов и доменных границ (стенок) – все это входит в понятие «доменная структура» магнетика.

С тех пор, как впервые наблюдались магнитные домены, исследования доменных структур путем непосредственного наблюдения доменов шли с нарастающей интенсивностью. Обнаружилось огромное разнообразие доменных структур в кристаллах различных веществ. Более того, оказалось, что для одного и того же вещества, но в образцах разного размера и формы, доменная структура может быть совершенно различной. Своеобразные домены наблюдаются в поликристаллических и аморфных тонких слоях, лентах и пленках с наведенной магнитной анизотропией.

Домены различаются не только по виду, но и по своим свойствам. Например, есть доменные структуры, исключительно чутко откликающиеся на внешние воздействия, особенно на магнитные поля. И наоборот, есть структуры, изменить которые очень трудно. Таким образом можно говорить о целом мире магнитных доменов.

При последовательном изменении напряженности магнитного поля Н от +Нs – значения поля насыщения одного направления до –Нs – поля противоположного направления домены «рождаются», растут, развиваются, начинают взаимодействовать друг с другом, изменяют свою форму и размеры. Потом те домены, в которых намагниченность Js ориентирована удачно относительно поля (например, JsН) постепенно поглощают соседние домены (с Js¯Н).

Векторы спонтанной намагниченности в кристалле ориентируются не как угодно, а строго вдоль определенных кристаллографических осей. Их называют осями легкого намагничивания(ОЛН) , так как в этих направлениях кристалл намагничивается легче (в меньших полях), чем в любых других. В этом проявляется естественная магнитокристаллическая анизотропия.

Количество осей легкого намагничивания в разных магнетиках различно. Например, железо (Fe) имеет кубическую кристаллическую решетку, и осями легкого намагничивания служат ребра куба. Их обозначают [100], [010] и [001], так что у Fe три естественных оси легкого намагничивания. Никель (Ni) также имеет кубическую решетку, но осями легкого намагничивания являются пространственные диагонали куба, их четыре. Кобальт (Со) имеет гексагональную кристаллическую решетку и единственную ОЛН – гексагональную ось. Кристаллы различных веществ по характеру магнитной анизотропии могут быть подобны Fe или Ni и их называют магнитомногоосными, а те, которые подобны Со, - магнитоодноосными.

Наряду с естественной магнитной анизотропией в кристалле можно искусственно создать так называемую наведенную магнитную анизотропию. Например, в монокристаллическом образце Fe в форме сферы (это изотропная форма) три ОЛН – [100], [010] и [001] – равноправны. Но в образце в форме тонкой пластинки, перпендикулярной оси [001], эта ось уже не является осью легкого намагничивания. Действительно, намагнитить пластинку вдоль этой оси гораздо труднее, чем вдоль осей [100] и [010], лежащих в плоскости пластинки. Так, из-за анизотропии формы образец из магнитотрехосного стал магнитодвухосным. Если теперь пластинку слегка растянуть вдоль [100], т.е. создать одноосные упругие направления, то эта ось станет легчайшей, а образец – магнитоодноосным.

Рассмотрим однородно намагниченный вдоль оси легкого намагничивания кристалл (рисунок 35а). В этом состоянии образец, подобно постоянному магниту, создает поле (Нm), обладающее большой энергией (Еm). Как любая термодинамическая система кристалл стремится перейти в равновесное состояние с минимумом энергии. Есть ли возможность уменьшить энергию Еm? Да, есть. Эту энергию можно уменьшить примерно в два раза, если в образце возникнут два домена (рисунок 35б). Заметьте, если на рисунке 35а образец намагничен до насыщения (J = Js), то в состоянии на рисунке 35б он размагничен (J=0). Отсюда понятно, почему поле Н называют размагничивающим, а энергию Еm – магнитостатистической, или размагничивающей, энергией. Можно и дальше понизить Еm, если увеличить число доменов (рисунок 35в). Однако, начиная с состояния на рисунке 35б, появляется новый объект – доменная граница («стенка»). В стенке происходит поворот Js от направления «вверх», до направления «вниз» (на рисунке 35б), т.е. отклонение Js от ОЛН и соответственно появление энергии магнитной анизотропии. Общая граничная энергия Еg = gS, где g– энергия, приходящаяся на единицу площади стенки, S – суммарная площадь всех стенок. Таким образом, увеличивая число доменов, выигрываем в Еm и проигрываем в Еg. В итоге в равновесном состоянии в кристалле сформируется такая доменная структура (с таким числом доменов), которая обеспечивает минимум его суммарной энергии.[6, с. 7-8]

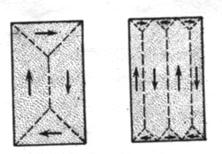
Рисунок 35 - Схема образования магнитных доменов

Могут возникнуть доменные структуры, в которых магнитный поток целиком замыкается внутри образца [4, с.140-141].

На рисунке 36 структуры имеют нулевую магнитную энергию. Здесь границы «замыкающих доменов», имеют форму трехгранных призм вблизи концевых граней кристалла, образуют углы по 450 с намагниченностью «своих» доменов и с намагниченностью соседних (900-ное соседство). Компоненты намагниченности в направлении, нормальном к границе, не претерпевает разрыва на границе, и никаких магнитных полей, связанных с намагниченностью, не возникает. Магнитный поток замыкается внутри кристалла, отсюда и термин «замыкающие домены» для доменов у поверхности кристалла, становящихся элементом магнитной цепи.

Рисунок 36.

Наблюдаемые доменные структуры часто имеют гораздо более сложный характер, чем в описанных выше простых примерах, но их образование всегда связано с уменьшением энергии системы и переходом от конфигурации насыщения, обладающей большой магнитной энергией, к некоторой доменной конфигурации с меньшей энергией [8, с. 586-587].

1.13 Размеры доменов и границ

Причина разбиения ферромагнетиков на домены – это конкуренция обменных и магнитных сил в них: обменные силы стремятся установить магнитные моменты атомов параллельно, а магнитные силы (размагничивающие) антипараллельно. В результате этого образуется магнитная структура, обладающая минимумом магнитной энергии (замкнутая магнитная конфигурация). На рисунке 35 схематически показан последовательный переход от менее выгодной магнитной конфигурации к более выгодной на рисунке 36.

Следует указать, что границы между доменами, показанные на рисунке 35б,с и рисунке 36 энергетически невыгодны, так как здесь существует слишком большой скачек обменной энергии при переходе от одного домена к другому. Должен существовать слой между доменами, в котором магнитные моменты атомов M постепенно изменяют свое направление (рисунок 37), причем с выходом из плоскости (так называемая блоховская граница). Это приводит к плавному изменению обменной энергии при переходе границы. С другой стороны, поскольку изменение направлений M в граничном слое происходит в кристалле, все большее число атомов будет обладать магнитными моментами, не ориентированными в направлении легкого намагничивания С (рисунок 37), и тем самым они должны увеличивать энергию магнитной анизотропии. В результате граница приобретает такую ширину б, при которой сумма обменной энергии и энергии магнитной анизотропии будет минимальной [1, с. 61-62].

Рисунок 37.

Доменные стенки можно разделить на два типа: 180-градусные, направление намагниченности в которых меняется при переходе от одной стороны стенки к другой на 1800 (рисунок 37), и 90-градусные, в которых направление намагниченности меняется только на 900 [9, с. 185].

Упрощенный расчет для ширины граничного слоя в случае 1800 – соседства для одноосного кристалла дает:

δ = p (27)

где А – обменный интеграл,

К – константа магнитной анизотропии,

a – постоянная решетки.

Подстановка соответствующих значений показывает, что δ= 10-5 см или, иными словами составляет десятые доли микрона, что совпадает с данными опыта.

Образование граничных слоев, естественно, происходит с затратой некоторого количества энергии, пропорционально площади граничного слоя. Как показывает расчет, плотность граничной энергии, т.е. энергия единицы поверхности граничного слоя, равна:

γ= p (28)

Подстановка численных значений показывает, что плотность граничной энергии лежит в пределах от 0,1 до 10 эрг/см2.

Ширина домена, зависит от величины кристалла. Расчет дает, что ширина домена d равна:

d =  , (29)

где L – длина кристалла.

Таким образом, крупные домены могут быть получены лишь в крупных кристаллах. В очень мелких кристаллах доменной структуры вообще не возникает, они являются однодоменными [7, с. 84-85].

Следует заметить, что в тонких магнитных пленках в направлениях, перпендикулярных плоскости пленки, существует большое размагничивающее поле (анизотропия формы), и поэтому реализуется доменная граница без выхода вектора M из плоскости (Неелевская граница) [1, с. 62].

2. Методы исследования

2.1 Метод порошковых фигур

При приготовлении ферромагнитных образцов, используемых для наблюдения доменов, следует учитывать два момента.

Во-первых, доменная структура может значительно изменяться в зависимости от формы образца и в особенности в зависимости от кристаллографической ориентации рассматриваемой плоскости.

Во-вторых, сильное влияние на доменную структуру оказывает деформация поверхности. Имея в виду первое замечание, для наблюдения четкой доменной структуры желательно использовать по возможности либо поликристалл с максимально большими кристаллическими зернами, либо монокристалл.

В большинстве случаев монокристаллы достаточно большой величины получают путем медленного перевода расплава в твердое состояние. Затем с помощью оптического или рентгеновского метода определяют кристаллографические направления и вырезают образец вдоль главной кристаллографической поверхности.

На рисунке 38 приведено изображение доменной структуры, которое наблюдается на поверхности образца, не совпадающей с главной кристаллографической плоскостью. Интерпретировать этот случай довольно трудно. Имея в виду второе замечание, необходимо достаточно хорошо отшлифовать изучаемую поверхность наждачной бумагой, затем отполировать ее окисью хрома и, наконец, провести электрополировку [9, с.159].

На отполированных образцах можно наблюдать изображения доменов. Для наблюдений можно использовать отражательный металлографический микроскоп с увеличением 70¸150×. Для таких исследований очень хорошо иметь небольшой магнит типа показанного на рисунке 39. С его помощью можно создавать любое необходимое поле. Впрочем, для наблюдений изображений доменов достаточно и простого постоянного магнита, расположенного под предметным столиком.

Рисунок 38. Изображение доменов, наблюдавшееся на кристаллической плоскости, расположенной под углом к главной плоскости (на монокристаллическом образце 4% Si-Fe)

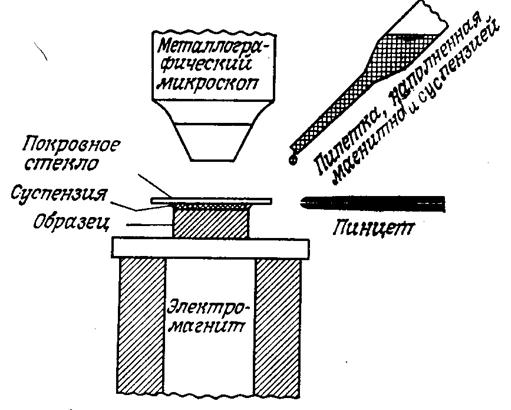
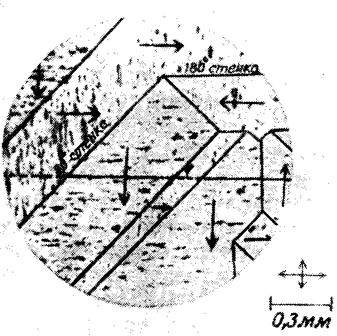
Рисунок 39 - Электромагнит, применяемый при наблюдении доменов.

Электролитически отполированный образец помещают над магнитом, наносят на него сверху с помощью пипетки одну – две капли суспензии и, наложив сверху покровное стекло, изучают образец под микроскопом (рисунок 40). Частицы суспензии притягиваются к границам между доменами, образуя здесь черные линии. На рисунке 41 приведено изображение доменов, наблюдавшихся таким способом на поверхности (001) образца 4 % Si – Fe. Черные линии – границы доменов, а стрелки указывают направление намагниченности в отдельных доменах. Направление намагниченности проще всего определить, используя то, что она перпендикулярна полоскам, которые в большом количестве видны внутри доменов. Полоски могут появляться на неровностях, возникающих на поверхности при электрополировке, или на неоднородностях концентрации сплава в образце, поскольку в этих местах возникают магнитные полюсы, или их еще называют линиями насыщения [9, с. 160-161].

Рисунок 40 - Метод наблюдения порошковых фигур.

Рисунок 41 - Изображение доменов, наблюдавшееся на монокристалле 4% SI-Fe в плоскости (001). Границы доменов обведены тушью (чёрные линии). Горизонтальной линией в середине рисунка показано, как выглядит царапина, сделанная механическим способом.

Возникновение линий насыщения можно объяснить следующим образом. Как бы хорошо ни была отполирована поверхность кристалла, она всегда имеет дефекты типа царапин. Эти царапины на поверхности расположены во всех направлениях, однако выявляются они с помощью магнитного порошка далеко не во всех случаях.

Если направление царапины совпадает с вектором намагниченности, то никаких магнитных полюсов не образуется и магнитный порошок на такой царапине не оседает (рисунок 42б).

Если же царапина направлена перпендикулярно вектору намагниченности, то на этой царапине магнитные полюса, на которых оседает магнитная суспензия (рисунок 42а). Таким образом, магнитный порошок будет выявлять царапины, перпендикулярные направлению намагниченности, и, наоборот, по выявленным царапинам (линиям насыщения) можно судить о направлении линии, вдоль которой лежит вектор намагниченности в домене.

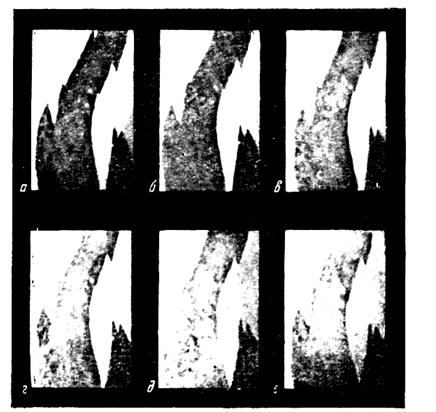
Рисунок 42. Магнитные силовые линии в окрестности царапины в случае, когда царапина перпендикулярна (а) и параллельна (б) направлению намагниченности.

При наложении на образец магнитного поля или упругих напряжений его доменная структура изменяется. Домены, намагниченность которых направлена противоположно направлению поля или составляет с ним тупой угол, начинают уменьшаться. Этот процесс идет обычно путем смещения границ, и кристалл в целом приобретает все возрастающую намагниченность.

Такое смещение границ под действием поля возможно, очевидно, до тех пор, пока наиболее выгодно ориентированные в отношении поля домены не поглотят полностью домены, ориентированные менее выгодно. После завершения процесса смещения кристалл оказывается намагниченным однородно до насыщения в направлении ближайшей к полю оси легкого намагничивания.

Такой процесс смещения границ при нарастании намагничивающего поля можно проследить с помощью киносъемки порошковых фигур. На рисунке 43 представлены кадры из кинофильма, показывающие изменения порошковых фигур в непрерывно возрастающем магнитном поле, направленном вдоль одной из осей легкого намагничивания. Следует отметить, что с помощью метода порошковых фигур нельзя проследить за быстрыми изменениями доменной структуры, которые происходят, например, при положении переменного поля обычной частоты в 50 гц. Это связано с инерционностью магнитного порошка, неуспевающего следовать за быстрыми перемещениями междоменных границ.

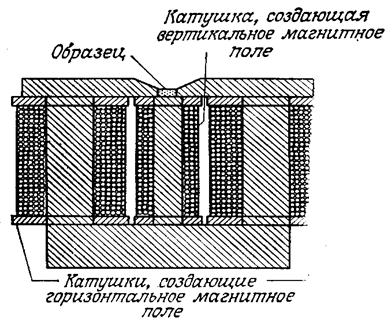
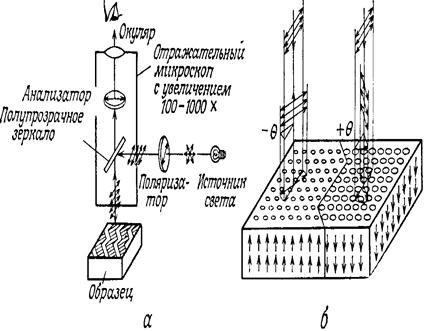
Рисунок 43.

Метод порошковых фигур обладает еще и тем недостатком, что его использование для исследования доменной структуры ограничено небольшим интервалом температур, близким к комнатной. Для изучения доменной структуры в области высоких температур жидкая суспензия, очевидно, неприменима.

В настоящее время разработаны новые методы изучения доменной структуры, некоторые из них свободны от недостатков, свойственных методу порошковых фигур [7, с. 81-82].

2.2 Магнитооптический метод

Свет, как известно, имеет волновую природу, причем световые волны есть волны поперечные, т.е. колебания в световой волне направлены перпендикулярно линии распространения светового луча. В обычном естественном свете эти поперечные колебания совершаются перпендикулярно направлению луча в самых разнообразных плоскостях.

Если на пути светового луча поставить особый прибор называемый поляризатором, то он выделит световые волны, колебания которых происходят в строго определенной плоскости. Такая световая волна называется поляризованной.

Если на пути поляризованного света поставить еще один поляризующий прибор (анализатор), то свет через него пройдет полностью только в случае, если поляризатор и анализатор расположены одинаково. Если же расположение их неодинаково, то свет через них пройдет лишь частично. При «скрещенных» поляризатора и анализатора, когда они расположено под углом 900 относительно друг друга, свет через них вообще не проходит [7, с. 82-83].

Магнитооптический метод наблюдения доменов с помощью магнитооптических эффектов Керра или Фарадея не требует использования промежуточной среды типа суспензии, поэтому он удобен для исследования доменов при различных температурах.

Магнитооптический эффект Керра заключается в том, что при отражении падающего на намагниченный магнетик поляризованного света происходит поворот плоскости поляризации. Рисунок 44 поясняет принцип действия установки для наблюдения доменов с помощью магнитооптического эффекта Керра. На рисунке 44а изображена схема установки. Свет от источника, проходя поляризатор, поляризуется и, отразившись от полупрозрачного зеркала, падет на образец перпендикулярно его поверхности. Отраженный от поверхности образца поляризованный свет, пройдя полупрозрачное зеркало, попадает на анализатор, который пропускает только компоненту, параллельную оси анализатора. Затем поляризованный свет попадет в окуляр, через который производится визуальное наблюдение. Если ферромагнитный образец разбит, как показано на рисунке 44б, на домены, в которых направление спонтанной намагниченности перпендикулярно поверхности образца, то благодаря магнитооптическому эффекту Керра в доменах с антипараллельной намагниченностью поворот плоскости поляризации произойдет в противоположных направлениях. Следовательно, изображение домена в отраженном свете будет светлым, если направление поляризации отраженного от него света совпадает с направлением оси пропускания анализатора, и темным в обратном случае.

Рисунок 44. а – установка для наблюдения доменов с помощью магнитооптического эффекта Керра; б – поворот плоскости поляризации света, отражённого доменами ферромагнитного образца, ось лёгкого намагничивания которого перпендикулярна поверхности.

На рисунке 45 показано изображение доменов MnBi в плоскости с, полученное этим методом. В MnBi ось с является легкой осью, причем константа анизотропии очень велика. Поэтому размагничивающее поле, создаваемое возникающими на поверхности магнитными полюсами, не оказывает заметного влияния и намагниченность доменов направлена перпендикулярно поверхности. На рисунке 45а-в показаны домены в образцах разной толщины. Как мы видим, изображение меняется сильно.

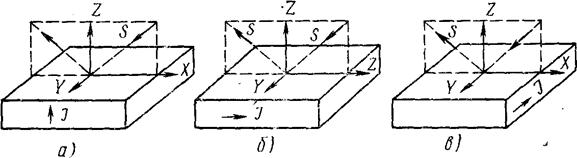
Рисунок 45 - Изображение доменов с плоскости образца MnBi, полученное с помощью магнитооптического эффекта Керра. а – толстый образец; б, в – образцы с последовательно уменьшающейся толщиной.

Если направление намагниченности параллельно поверхности образца, метод, схема которого представлена на рисунке 44, не дает результатов. В этом случае для наблюдения доменов с помощью магнитооптического эффекта Керра свет посылают на поверхность образца под углом и используют то обстоятельство, что направление поворота плоскости поляризации зависит от знака проекции вектора намагниченности на направление распространения света (в такой геометрии проявляется меридиональный эффект Керра). Оптическая система, включающая анализатор и окуляр, очевидно, должно быть расположена зеркальносимметрично падающему лучу [9, с. 163-165].

При отражении линейного поляризованного света от намагниченной поверхности плоскость поляризации света поворачивается на угол, величина которого зависит от направления намагниченности образца. Вращение плоскости поляризации света при отражении его от поверхности намагниченного ферромагнетика называется магнитооптическим эффектом Керра. В зависимости от взаимного расположения вектора намагничивания в плоскости ферромагнитного образца и плоскости падения света различают полярный, меридиональный и экваториальный эффекты Керра.

Полярный эффект Керра: вектор намагничения перпендикулярен поверхности ферромагнитного зеркала, но параллелен плоскости падения света (рисунок 46а). Меридиональный (продольный) эффект Керра: вектор намагничения находится в плоскости зеркала и параллелен плоскости падения света (рисунок 46б). Экваториальный (поперечный) эффект Керра: вектор намагничения расположен в плоскости зеркала, но перпендикулярен плоскости падения света (рисунок 46в) [2, с.124-125].

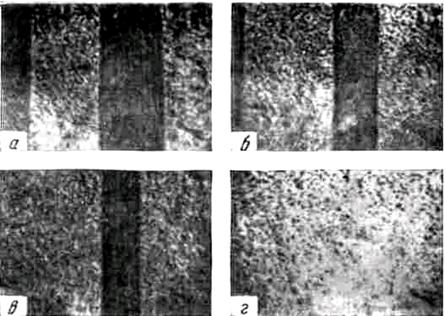
Рисунок 46.

Как было показано Керром, при отражении поляризованного света от намагниченного ферромагнетика плоскость поляризации света несколько изменяется в зависимости от направления и величины намагниченности.

Поскольку намагниченность в различных доменах ферромагнитного кристаллита направлена по-разному, то и плоскость поляризации отраженного света от них повернется на различные углы, и от различных доменов через анализатор пройдет свет различной интенсивности.

При фокусировке изображения кристаллита на фотопластинку домены, намагниченность в которых направлена по-разному, будут представлены в виде полос различной освещенности.

На рисунке 47 изображена фотография доменной структуры кристалла кремнистого железа. В отсутствие магнитного поля доменная структура представляет собой темные и светлые полосы равной ширины (а). При наложении магнитного поля размеры доменов изменяются (б-в).

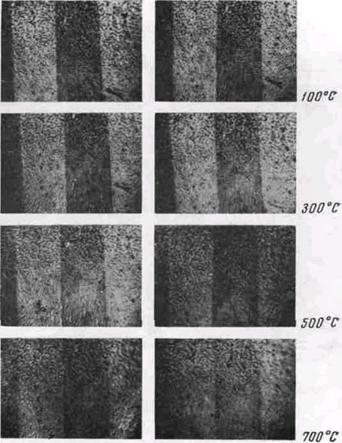
Рисунок 47 - Доменная структура кристалла кремнистого железа в нарастающем магнитном поле. С увеличением магнитного поля ширина темных доменов уменьшается вплоть до их полного исчезновения

Домены, изображенные на рисунке в виде темных полос, уменьшаются, из чего можно заключить, что они невыгодно ориентированы в отношении поля. В достаточно сильном поле эти домены исчезают (г).

На рисунке 48 приведены фотографии доменной структуры того же кристалла в отсутствие поля при различных температурах, вплоть до 7000 С.

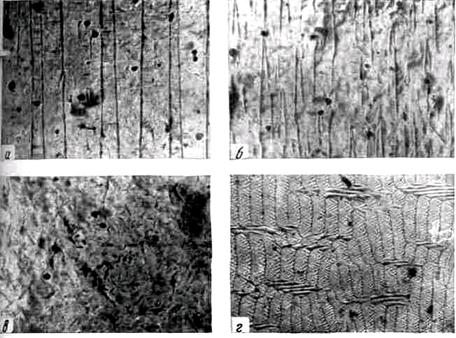
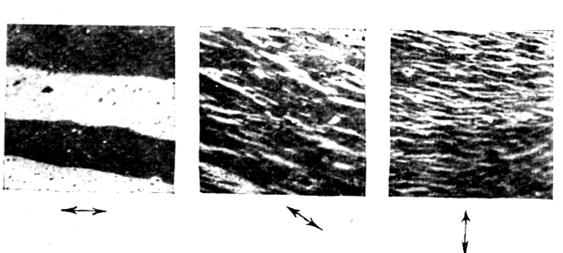
Рисунок 48 - Доменная структура кристалла кремнистого железа в отсутствие магнитного поля при различных температурах

Как видно из рисунка, доменная структура в этом случае обладает высокой температурной стабильностью (ширина доменов практически остается без изменений).

При наложении механических напряжений доменная структура также изменяется. Если напряжения однородны, она обычно становится более «правильной». Границы доменов представляют собой параллельные, равностоящие друг от друга линии. Иногда же при наложении напряжений доменная структура перестраивается и принимает совершенно иной вид. Характер изменения доменной структуры зависит от величины напряжений и их направления относительно осей кристалла.

На рисунках 49 и 50 показано изменение доменной структуры под действием напряжений. Что касается размеров доменов в отдельных кристаллах, то они зависят от размеров самого кристалла [7, с. 83-84].

Рисунок 49. Под действием напряжений доменная структура вида а превращается в структуру вида 6

Рисунок50 - Изменение доменной структуры под действием напряжений: а – σ = 0; б – σ = 8; в – σ = 12,5; г – σ = 19 кг/мм²

Эффект Фарадея заключается в том, что при прохождении плоскополяризованного света через вещество, магнитное поле в котором не равно нулю, возникает вращение плоскости поляризации. Очевидно, эффект Фарадея можно использовать лишь для исследования прозрачных сред. При изучении доменной структуры он может быть применен для очень тонких прозрачных ферромагнитных пленок.

Направление вращения плоскости поляризации зависит от направления намагниченности в домене. Если при исследовании структуры с антипараллельными доменами поляризатор и анализатор скрещены для доменов одного из направлений намагниченности, т.е. свет от этих доменов не проходит, то для доменов противоположного направления намагничености вследствие различного направления вращения плоскости поляризации свет через анализатор пройдет. Таким образом, доменная структура будет видна в виде темных и светлых полос доменов противоположной намагниченности.

Характерно то, что здесь выявляются сами домены, а не границы между доменами, как в случае метода порошковых фигур.

На рисунке 51 приведена фотография доменной структуры ферромагнитной пленки толщиной 500Ǻ, выявленная с помощью эффекта Фарадея.

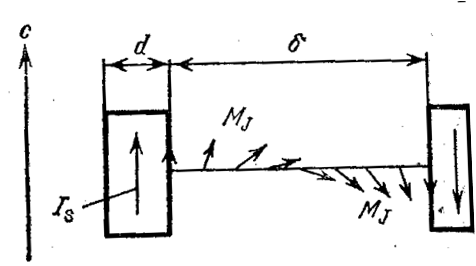
Рисунок 51 - Доменная структура тонкой ферромагнитной пленки, выявленная с помощью эффекта Фарадея.

Отличие от магнитооптического эффекта Керра состоит лишь в том, что на анализатор попадает свет, прошедший сквозь образец. В остальном используется такая же принципиальная схема, как и в случае магнитооптического эффекта Керра (см. рисунок 44) [9, с. 165].

Пусть к магнетику длиной L приложено магнитное поле Н. В общем случае угол поворота плоскости поляризации q пропорционален L и Н, т.е. имеет место следующее соотношение:

q=V·L·H (30)

Коэффициент пропорциональности V называется коэффициентом Верде [9, с. 373].

Постоянная Верде зависит от свойств вещества, температуры и частоты света [1, с.78].

2.3 Метод лоренцевой электронной микроскопии

При исследовании доменной структуры тонких ферромагнитных пленок, как и в случае массивных ферромагнетиков, могут быть использованы методы порошковых фигур и магнитооптический эффект Керра. Для достаточно тонких пленок (толщиной менее 1000Ǻ) можно использовать, как указывалось выше, магнитооптический эффект Фарадея и методы электронной микроскопии.

В настоящее время методы электронной микроскопии исследования доменной структуры тонких ферромагнитных пленок получили широкое распространение. С помощью электронного микроскопа могут быть выявлены как сами домены, так и их границы, причем независимо от направления поворота вектора намагниченности в граничном слое соседние граничные слои оказываются попеременно темными и светлыми, что легко понять, рассмотрев ход пучка электронов через пленку, разбитую на домены (рисунок 52).

Рисунок 52 - Электронно-оптическое выявление граничных слоёв в тонких ферромагнитных плёнках.

В самом деле, пусть на пленку, перпендикулярно ее поверхности, падает параллельный пучок электронов. На рисунке 52 изображены три домена, разделенные двумя 180-градусными границами 1 и 2. В крайних доменах вектор намагниченности направлен за плоскость чертежа, в среднем домене – в направлении к читателю. Пользуясь известным правилом левой руки, легко убедиться, что проходя сквозь пленку, электроны будут отклоняться так, как это показано на рисунке, т.е. крайние домены будут отклонять электроны влево, средний домен – вправо. На экран АВ, таким образом, электроны под граничным слоем 1 не попадут и его изображение будет темным; под граничным слоем 2, наоборот, попадет избыточное (в –сравнении с другими участками пленки) число электронов и изображение границы 2 будет светлым. Таким образом оказывается возможным выявлять граничные слои доменов и вести исследования доменной структуры тонких ферромагнитных пленок. Как показывают исследования динамики доменной структуры в магнитном поле, намагничивание и перемагничивание тонких ферромагнитных пленок происходит несколько иначе, чем массивных ферромагнитных кристаллов, причем характерной чертой изменения доменной структуры в магнитном поле является ее необратимость.

В массивных ферромагнитных образцах процесс смещения границ может быть как обратным, так и необратимым. В случае обратимости междоменная граница при увеличении поля плавно движется в одну сторону, при уменьшении поля – в другую. В случае необратимости движение границ становится скачкообразным и иногда сопровождается перестройкой всей доменной структуры, о чем говорилось выше. Однако в массивных ферромагнетиках и в этом случае, хотя и с которым отставанием, все же происходит восстановление доменной структуры с изменением направления роста магнитного поля.

В тонких ферромагнитных пленках, как правило, дело обстоит иначе. На рисунке 53 изображена доменная структура кобальтовой пленки толщиной 1200Ǻ. Структура эта была получена путем многократного наложения знакопеременного поля с убывающей амплитудой. Предварительно пленка намагничивалась до насыщения в направлении оси легкого намагничивания магнитным полем +56 эрстед. Вся пленка представляла собой, таким образом, один «светлый» домен.

Рисунок 53 - Доменная структура кобальтовой плёнки.

При уменьшении магнитного поля до нуля поле оставалось светлым, так как вследствие прямоугольности петли гистерезиса намагниченность пленки не изменялась. В случае наложения на пленку поля противоположного направления при некотором значении поля на светлом фоне возникал темный клин – зародыш обратной намагниченности, который увеличивался с ростом поля и занимал значительную поверхность, ограниченную участками, обозначенными цифрами 1. Такой домен обратной намагниченности был получен в поле –54 эрстеда. При уменьшении отрицательного поля до нуля граница домена оставалась неподвижной. При наложении положительного поля в том месте, где возник зародыш отрицательной намагниченности, появляется клинообразный зародыш положительной намагниченности и внутри темного клина рост светлый. В поле, равным +48 эрстед, граница светлого клинообразного домена достигла положений, определяемых цифрами 2. При уменьшении положительного поля до нуля граница светлого клинообразного домена оставалась неподвижной. При последующем наложении соответственно полей в –47 и +43 эрстеда получались новые клинообразные домены внутри прежних.

Рисунок 54. Доменная структура тонкой ферромагнитной плёнки при её размагничивании под различными углами к оси лёгкого намагничивания (направление осей лёгкого намагничивания показано стрелками)

Из сказанного вытекает, что доменная структура тонких ферромагнитных пленок существенно зависит от способа изменения поля. На рисунке 54 показана доменная структура железной пленки при размагничивании ее под различными углами к оси легкого намагничивания. Как видно из этого рисунка, доменная структура при размагничивании под разными углами оказывается совершенно различной.

На рисунке 55 показан процесс намагничивания вдоль легкой оси тонкой железной пленки путем смещения границ. Светлые домены растут за счет темных. При намагничивании под углом к оси легкого намагничивания намагничивание осуществляется не только путем смещения границ, но и перестройки доменной структуры (рисунок 56).

Рисунок 55 - Намагничивание тонкой ферромагнитной плёнки путём смещения доменных границ.

Рисунок 56 - Намагничивание под углом к лёгкой оси (перестройка доменной структуры)

В отсутствие поля доменная структура тонких ферромагнитных пленок обладает высокой температурной стабильностью. На рисунке 57 показана доменная структура железной пленки толщиной 1600Ǻ при различных температурах (от –100 до +6500 С). Как видно из рисунка, и исследованном интервале температур доменная структура не изменяется, что весьма важно при использовании тонких ферромагнитных пленок в счетно-решающих системах.

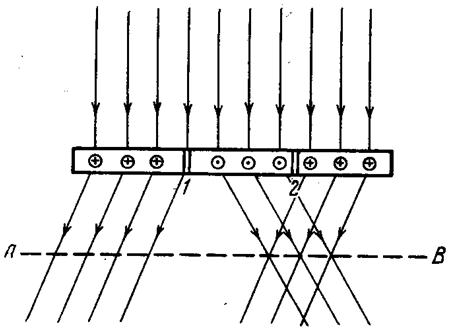
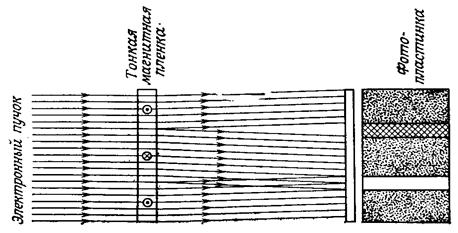
Рисунок 57 - Доменная структура тонкой железной плёнки при различных температурах: а – 100; б – 200; в – 250; г – 350; д – 500; е - 650ºС

Что касается граничных слоев, то в достаточно толстых пленках они ничем не отличаются от граничных слоев в массивных монокристаллах. В таких граничных слоях вектор намагниченности остается в плоскости граничного слоя и в центральной его части оказывается направленным перпендикулярно поверхности пленки. Такие границы называют границами Блоха.

В очень тонких ферромагнитных пленках вектор намагниченности в граничном слое все время остается в плоскости пленки, медленно поворачиваясь на 1800 в случае антипараллельных доменов. Такие границы получили название границ Нееля.

При промежуточных толщинах (для пермаллоевых пленок от 900 до 400Ǻ) структура граничных слоев оказывается более сложной [7, с.136-141].

Доменную структуру тонких магнитных пленок, сквозь которые проходит электронный пучок, можно наблюдать с помощью электронного микроскопа. Принцип метода иллюстрируется на рисунке 58. Электронный пучок, проходя через тонкую пленку, испытывает влияние силы Лоренца, вызванной спонтанной намагниченностью, и отклоняется в разных доменах на разные углы. В результате в фокальной плоскости проекционной электронной линзы, расположенной на некотором расстоянии от тонкой пленки, образуется изображение доменных стенок в виде черных или светлых линий. Такой метод называют методом лоренцевской электронной микроскопии. На рисунке 59 показано изображение доменов в тонкой пленке из пермаллоя толщиной 600Ǻ, полученное таким методом.

Рисунок 58 - Принцип метода лоренцевой микроскопии.

Рисунок 59 - Изображение доменов в тонкоплёночном образце из пермаллоля имеющем толщину 600Ǻ, полученное по методу лоренцевой микроскопии.

Если фокус проекционной линзы, применяемой в лоренцевской микроскопии, находится на бесконечности, электронные пучки, имеющие одно направление, образуют точечное изображение (дифракционное пятно), что позволяет одновременно наблюдать распределение направлений намагниченности по всему образцу. На рисунке 60 видно, как изменилось направление электронного пучка при прохождении через монокристаллическую тонкую пленку железа, параллельную плоскости (001). Из рисунка 60 видно, что в указанной плоскости имеется четыре направления намагниченности. Таким методом можно получать информацию о распределении спинов в доменных стенках. Преимущество лоренцевской микроскопии заключается в том, что она позволяет повысить увеличение, однако у нее есть и недостаток, состоящий в том, что исследуемые образцы должны иметь небольшую толщину, поскольку описанный метод применим только к образцам, сквозь которые может проходить электронный пучок [9, с. 165-167].

Рисунок 60 - Изображение доменов в тонкой плёнке (2550Ǻ), параллельной плоскости (001), и картина отклонений электронного пучка.

Заключение

В настоящее время разработано много экспериментальных методик для визуального наблюдения доменной структуры, как на поверхности ферромагнитного образца, так и частично в его толщине. Наиболее простым является метод порошковых фигур. Но метод порошковых фигур имеет ряд недостатков. Его использование ограниченно небольшим интервалом температур, близким к комнатной. Так же с его помощью нельзя проследить за быстрым изменением доменной структуры. Это связано с инерционностью магнитного порошка, не успевающего следовать за быстрыми перемещениями междоменных границ.

Для наблюдения доменной структуры можно также применять магнитооптические методы, основанные на явлениях Керра и Фарадея. В отличае от метода порошковых фигур, магнитооптические методы дают нам возможность видеть всю поверхность доменов, а не только их граничные слои. При исследовании доменной структуры тонких ферромагнитных пленок, как и в случае массивных ферромагнетиков, могут быть использованы метод порошковых фигур и магнитооптический эффект Керра.

Для достаточно тонких пленок (толщенной менее 1000 А) можно использовать магнитооптический эффект Фарадея и методы электронной микроскопии. В настоящее время методы электронной микроскопии исследования доменной структуры тонких ферромагнитных пленок получили широкое распространение. С помощью электронного микроскопа могут быть выявлены как сами домены, так и их границы, причем независимо от направления поворота вектора намагниченности в граничном слое соседние граничные слои оказываются попеременно темными и светлыми. Электронно-микроскопический метод изучения доменной структуры позволяет определить даже небольшие нарушения однородности намагниченности внутри самих доменов в ферромагнитной пленке .

Метод магнитного порошка с успехом используется для анализа механических, химических и структурных неоднородностей поверхностей ферромагнитных материалов.

Магнитооптический эффект Керра можно использовать для изучения динамических свойств ферромагнетиков, в частности ферромагнитных пленок. Так как все магнитооптические эффекты связаны между собой, целесообразно выбрать те из них, которые легче наблюдать экспериментально. С этой точки зрения наиболее удобны исследования магнитооптических эффектов при меридианном и экваториальном намагничивании. В случае же полярного эффекта Керра необходимо намагничивать пленку до насыщения перпендикулярно поверхности, то есть создавать большие магнитные поля.

Изучение структуры ферромагнитных пленок при помощи электронного микроскопа основано на взаимодействии электронов с магнитным полем намагниченных пленок. Поэтому этот метод позволяет более детально изучить структуру ферромагнитных пленок, чем метод порошковых фигур или магнитооптический метод, так как применяемые в них оптические микроскопы имеют на много меньшую разрешающую способность, чем электронный микроскоп.

Список литературы

1.         Белов К.П., Магнетизм на земле и в космосе/Белов К.П.,Бочкарёв Н.Г.- М: Наука,1983. – 192c.

2.         Буравихин В.А., Практикум по магнетизму/ Буравихин В.А., Шелковников В.Н., Карабанова В.П., М: Высш. шк., 1979. – 197с.

3.         Бушманов Б.Н., Физика твёрдого тела / Бушманов Б.Н., Хромов Ю.А., М: Высш. шк., 1971. – 224с.

4.         Вонсовский С.В., Магнетизм :Учебн.пособ. - М: Наука, 1984. – 208с.

5.         Каганов М.И., Природа магнетизма / Каганов М.И., Цукерник В.М.,

6.         М: Наука, 1982. – 192с.

7.         Кандаурова Г.С., Хаос, порядок и красота в мире магнитных доменов// Известия УрГУ - 1999 - №7 - С.4 - 5

8.         Киренский Л.В., Магнетизм / М: Наука, 1967. – 196с.

9.         Китель Ч., Введение в физику твёрдого тела, / Пер. с англ. - М: Наука, 1978. – 792с.

10.       Тикадзуми С.,Физика ферромагнетизма. Магнитные характеристики и практические применения / Пер. с японского – Москва: Мир, 1987. – 419с.