|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Дипломная работа: Классификация римских цифр на основе нейронных сетей
Данная сеть после обучения показывает хорошие обобщающие данные. Скорость обучения и начальный момент на качество обобщения не влияют. Сеть Ворда с двумя блоками в скрытом слое и с обходным соединением Структура НС: 1. количество слоев: 4 2. количество нейронов: а) во входном слое: 63 б) в выходном слое: 9 3. активационная функция а) во входном слое: линейная б) в выходном: логистическая В таблице отражена зависимость минимальной средней ошибки на тренировочном и тестовом наборах и времени обучения от вида функций активации. Скорость обучения = 0,1; момент = 0,1 Таблица данных
Исходя из таблицы дла данной сети оптимальными будут функции активации Гауссова для 1 слоя и Комплем. Гауссова для 2 слоя.
Данная сеть после обучения показывает не очень хорошие обобщающие данные. Скорость обучения и начальный момент на качество обобщения не влияют. Сеть Кохонена Структура НС: 1. кол-во нейронов a. входной слой: 63 b. выходной слой: 9 2. скорость обучения: 0,5 3. начальные веса: 0,5 4. окрестность: 8 5. эпохи: 500 в таблице отражена зависимость средней количества неиспользованных категорий от пораметров выбора примеров и метрик расстояния.
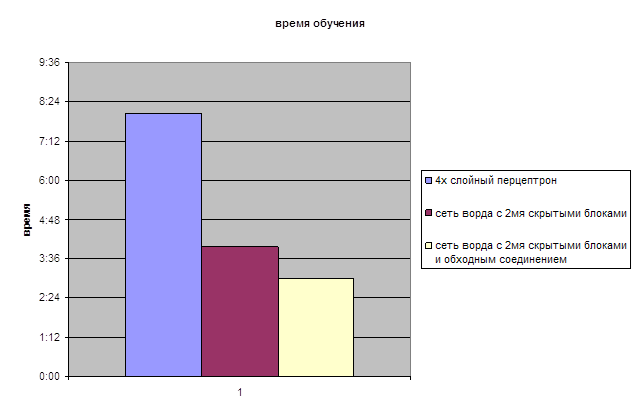
Данная сеть обладает плохим обобщением. На данной диаграмме показаны сравнительные данные по времени обучения рассмотренных сетей. Т.к сеть Кохонена обладает наихудшими обобщением, ее в диаграмму не включаем.
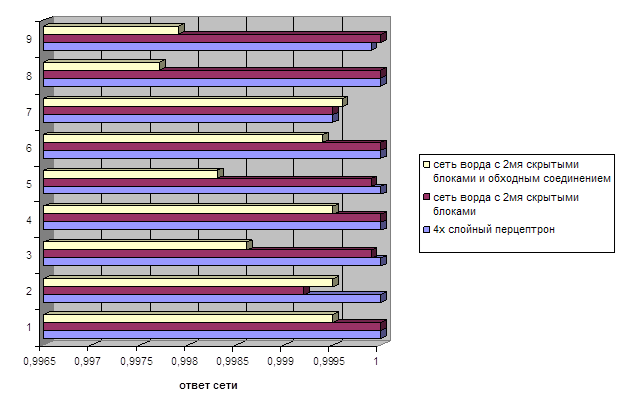
На данной диаграмме показаны сравниваемые нами значения выходных данных обученных сетей.
Исходя из представленных диаграмм оптимальной для нас будет сеть Ворда с 2мя скрытыми блоками. 2.3 Выбор параметров обучения
Находим оптимальные параметры: • скорость обучения в интервале от 0 до1 • момент в интервале от 0 до 1 • начальные веса от 0 до 1 1. Зависимость качества обучения от скорости обучения
2.Зависимость качества обучения от момента
3.Зависимость качества обучения от начальных весов
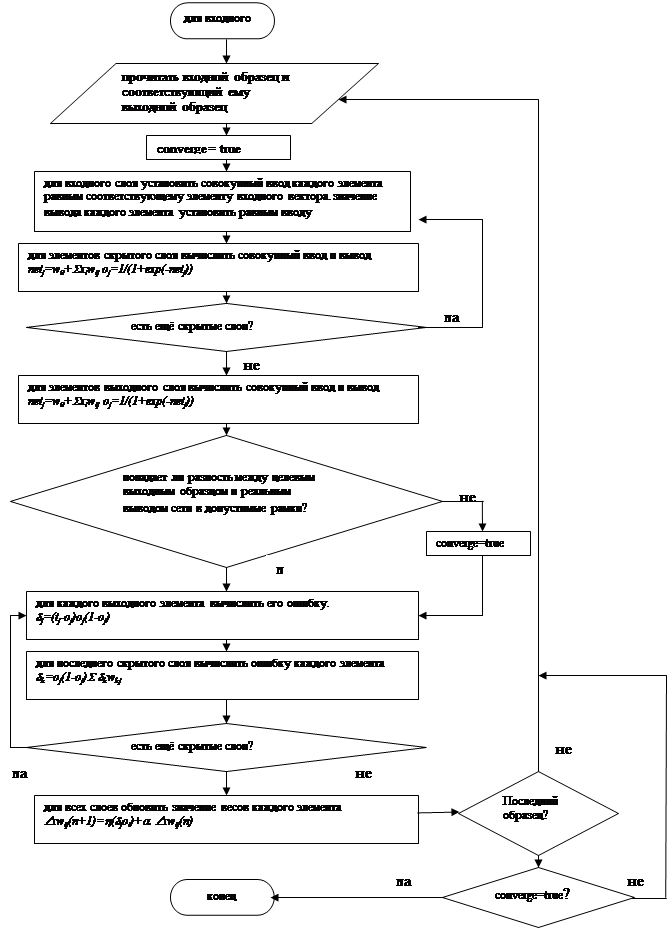
2.4 Оптимальные параметры обучения Скорость обучения: 0,1 Начальный момент: 0,1 Начальные веса: 0,3 Модель - Сеть Ворда с двумя блоками в скрытом слое. Структура НС: 1. количество слоев: 4 2. количество нейронов: 1) блок 1: 63 2) блок 2: 24 3) блок 3: 24 4) блок 4: 9 3. вид функций активации: 1) блок 1 – линейная [0;1] 2) блок 2 –гауссова 3) блок 3 –гауссова 4) блок 5 – логистическая. 2.5 Блок-схема алгоритма обучения
3. Анализ качества обучения При данных оптимальных параметрах результаты применения сети можно представить виде таблицы
Для проверки способностей к обобщению на вход сети подаются зашумленные последовательности входных сигналов. Процент зашумления показывает, какое количество битов входного вектора было инвертировано по отношению к размерности входного вектора. Для зашумления 5% сеть выдает такие результаты:
Далее мы подавали различное количество инвертированных битов. В таблице представлена зависимость количества инвертированных битов от количества правильных ответов на выходе
Таким образом мы выявили критическое количество зашумленных данных = 16 на каждый входной вектор. Это соответствует 20% зашумления. При большем зашумлении входных данных сеть не может отдать предпочтение одной цифре, причем с увеличением зашумления количество таких букв растет. Результаты сети при критическом зашумлении:
Судя по анализу качества обучения, сеть хорошо справляется при 20% зашумлении. Это говорит о том что у сети неплохой потенциал для обобщения. Выводы В ходе данной курсовой работы были получены навыки моделирования нейронных сетей, а также была решена частная задача моделирования нейронной сети для классификации римских цифр. Исходными данными для сети являлись изображения римских цифр, представленные виде матриц, размерностью 7х9. Обученная нейронная сеть хорошо себя показала при 20% уровне шума. Для увеличения этого показателя нужно снизить риск возникновения критических шумов. Этого можно достигнуть путем увеличения размерности сетки. Список использованных источников 1 Стандарт предприятия СТП 1–У–НГТУ–98 2 Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. – М.: Горячая линия – Телеком, 2001. – 382 с.:ил. 3 Электронный учебник по NeuroShell 2 4 Каллан Р. Основные концепции нейронных сетей 5 Ресурсы сети Интернет |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Страницы: 1, 2