|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Курсовая работа: Выпуклые фигурыКурсовая работа: Выпуклые фигурыСТАВРОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ Кафедра геометрии Курсовая работа на тему: «Выпуклые фигуры»
Выполнила студентка 2 курса ФМФ специальности «Физика» гр. «А» Валаева С.В.
Ставрополь 2007г. СОДЕРЖАНИЕ Введение...................................................................................................................3 Выпуклые фигуры………………………………………………………………...5 Кривые постоянной ширины и их применение....................................................7 Свойства кривых постоянной ширины...............................................................14 Литература.............................................................................................................17 ВВЕДЕНИЕ. Понятие выпуклости возникло в античные времена. Оно встречается в сочинениях Архимеда, «О шаре и цилиндре», есть такие слова: «Я называю выпуклыми в одну и ту же сторону такие поверхности, для которых отрезки, соединяющие две точки, будут... находиться по одну сторону от поверхности». В новое время изучение выпуклых фигур началось в XIX веке. Как отдельная ветвь геометрии, выпуклая геометрия родилась в трудах О.Коши, Я.Штейнера и Г.Минковского. У нас в стране задачи о выпуклых фигурах были популярны в довоенных школьных математических кружках. Выдающийся математик Лев Генрихович Шнирельман, один из организаторов математического кружка при Московском университете, избрал одной из тем для занятий выпуклую геометрию. Эта тема была подхвачена Давидом Шклярским, аспирантом мехмата, математиком, подававшим большие надежды, но не вернувшимся с войны. Шклярский придал кружку совершенно иную форму, сохранившуюся и до нашего времени. Основное внимание стало уделяться решению не-стандартных задач. Выпуклость оказалась благодатнейшей почвой для развития геометрических способностей: красота и значимость ее результатов сочетались с совершенной элементарностью постановок задач и средств их исследования. На базе многолетних занятий по выпуклости геометрии со школьниками и студентами И.М. Яглом и В.Г. Болтянский, участники кружка Шклярского, продолжившие его дело, написали замечательную книгу « Простейшие выпуклые фигуры». На Западе происходит настоящий «выпуклый бум», связанный с рождением нового направлении в теории экстремума, получившего названия линейного программирования. Это направление зародилось в нашей стране. Его родоначальником был Леонид Витальевич Канторович, удостоенный за свой вклад в теорию линейного программирования и экономику Нобелевской премии. Результаты Канторовича были переоткрыты на Западе, там было осознано значение выпуклых экстремальных задач при решении актуальных проблем экономики и военно-промышленного комплекса, многие исследователи приняли участие в развитии новой дисциплины, получившей название выпуклого анализа. Здесь мне хочется коснуться некоторых узловых тем выпуклого анализа, сделав упор на их геометрическую суть. Выпуклые фигуры.
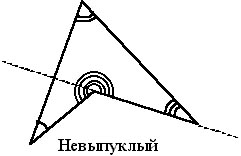
На рис.2 приведены примеры невыпуклых фигур.
Имеются полезные утверждения, которые справедливы для многоугольников независимо от того, выпуклы они или нет: 1. Сумма внутренних углов n-угольника (n ³ 3) равна 180° (n - 2). 2. n-угольник (n ³ 4) имеет ровно 3. Если
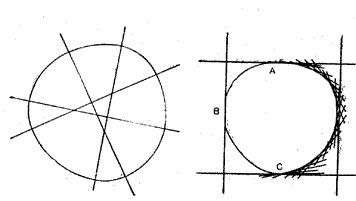
Кривые постоянной ширины и их применение. В повседневной жизни нередко возникает необходимость перевезти с места на место тяжелый предмет. Пользоваться при этом тележкой не всегда удобно: оси ее от большой нагрузки могут прогнуться и даже треснуть. В таких случаях тяжелый предмет кладут на плоскую платформу, установленную на цилиндрических катках. По мере продвижения платформы освободившиеся задние катки заносят вперед и укладывают перед ней. Ни сама платформа, ни покоящийся на ней предмет при движении по ровной горизонтальной поверхности не испытывают вертикальных перемещений по той простой причине, что цилиндрические катки в сечении имеют форму круга, а граница круга — окружность — принадлежит к числу замкнутых кривых, обладающих важным свойством — «постоянной шириной». Если замкнутую кривую поместить между двумя параллельными прямыми и двигать эти прямые до тех пор, пока они не коснутся нашей кривой, то расстояние между параллельными прямыми в момент касания будет называться шириной данной кривой в направлении, перпендикулярном параллельным прямым. Эллипс, очевидно, не имеет одинаковой ширины по всем направлениям: платформа, установленная на катках в форме эллиптического цилиндра, при движении испытывала бы вертикальные перемещения (моряки сказали бы «испытывала дифферент», то есть качку с носа на корму). Именно потому, что окружность имеет одинаковую ширину по всем направлениям, ее можно вращать между двумя параллельными прямыми, не изменяя расстояния между ними. Существуют ли другие замкнутые кривые постоянной ширины, помимо окружности? Большинство людей считают, что таких кривых нет, показывая, насколько сильно может вводить в заблуждение математическая интуиция. В действительности кривых постоянной ширины бесконечно много. Любая из них может служить поперечным сечением катка, по которому платформа будет катиться так же ровно, как и по цилиндру. Если бы кривые постоянной ширины не были открыты, незнание их привело бы к самым роковым последствиям в технике! Представим себе, что на кораблестроительном заводе собирают корпус подводной лодки, проверяя его
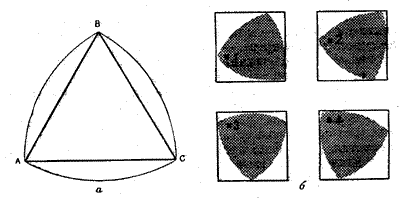
цилиндричность, промерами максимального диаметра по всем направлениям. Как мы вскоре узнаем, корпус мог бы быть чудовищно деформированным и тем не менее благополучно пройти подобные испытания. Именно поэтому цилиндричность корпуса подводной лодки проверяется специальными шаблонами. Простейшая кривая постоянной ширины, отличная от окружности, называется треугольником Рело в честь математика и инженера Франца Рело (1829—1905), преподававшего в Берлинской королевской высшей технической школе. Сама по себе эта кривая была известна математикам и до Рело, но именно он впервые доказал ее удивительное свойство — постоянство ширины. Если кривая постоянной ширины ограничена двумя парами параллельных прямых и одна пара пересекается с другой под прямым углом, то кривая постоянной ширины с необходимостью должна быть вписана в квадрат. Подобно окружности или любой другой кривой постоянной ширины, треугольник Рело может вращаться в квадрате, плотно прилегая к сторонам последнего, то есть все время касаясь всех четырех сторон квадрата (рис. 3,б). Читатель может убедиться в этом, вырезав треугольник Рело из картона и вставив его в квадратное отверстие надлежащих размеров. При вращении треугольника Рело внутри квадрата каждая из вершин треугольника проходит почти весь периметр квадрата. Небольшие отклонения имеются лишь вблизи вершин квадрата: углы получаются слегка закругленными. Треугольник Рело находит применение во многих механических устройствах, но ни в одном из них не используются его замечательные свойства кривой постоянной ширины. Лишь в 1914 году английский инженер Гарри Джеймс Уаттс изобрел инструмент, имевший в сечении форму треугольника Рело, для сверления квадратных отверстий. С 1916 года одна из фирм приступила к производству сверл Уаттса. «Мы все
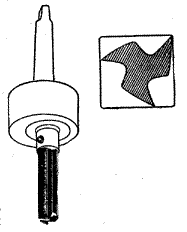
слыхали о гаечных ключах, приспособленных для гаек с левой резьбой, завязанных в узел водопроводных трубах и бананах из чугуна, — было написано в одной из рекламных листовок этой фирмы. — Мы считали подобные вещи смешными безделушками и отказывались даже верить, что они когда-нибудь встретятся нам в действительности. И вдруг появляется инструмент, позволяющий сверлить квадратные отверстия!» Сверло Уаттса изображено на рис. 4. Справа показано поперечное сечение сверла внутри квадратного отверстия. Сверление производится так. Сначала на металл накладывают металлический шаблон с квадратным отверстием нужных размеров. Сверло, вращаясь внутри отверстия в направляющей пластине (шаблоне), врезается кромками в металл и просверливает в нем квадратное отверстие. Как видно из рис.8, сверло Уаттса представляет собой просто-напросто треугольник Рело, в котором прорезаны углубления для отвода стружки и заточены режущие кромки. Когда треугольник Рело вращается, его центр не стоит на месте, поэтому патрон для зажима сверла Уаттса не должен препятствовать этому движению. Компания запатентовала специальный патрон со «свободно плавающим в нем сверлом», удовлетворяющий всем нужным требованиям. Из всех кривых
с заданной постоянной шириной треугольник Рело обладает наименьшей площадью.
Если ширина треугольника Рело равна
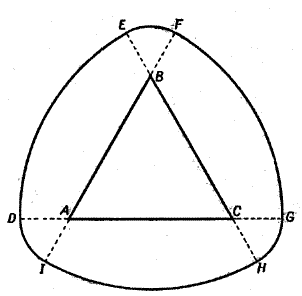
углы можно закруглить, продолжив каждую из сторон исходного (прямолинейного) равностороннего треугольника на одно и то же расстояние в обе стороны (рис. 5). Проводя дугу окружности с центром в вершине А, нужно увеличить раствор циркуля и провести затем еще одну дугу окружности (на этот раз FG) также с центром в вершине А. То же нужно проделать и в вершинах В и С. Полученная кривая будет по всем направлениям иметь ширину, равную сумме радиусов дуг, описанных из каждой вершины, то есть будет кривой постоянной ширины. Другие симметричные кривые постоянной кривизны вы построите, взяв вместо равностороннего треугольника правильный пятиугольник (или вообще любой правильный многоугольник с нечетным числом сторон) и проделав над ним аналогичную процедуру. Существуют способы, позволяющие строить и несимметричные кривые постоянной кривизны. Один из них состоит в следующем. Возьмите звездчатый многоугольник неправильной формы (число вершин у такого многоугольника непременно будет нечетным), образованный отрезками прямых равной длины (на рис. 6 показан звездчатый семиугольник). Поставив ножку циркуля в каждую вершину, проведите дугу окружности, соединяющую две противоположные вершины. Поскольку все дуги имеют одинаковый радиус, получившаяся кривая (на рис. 10, она показана жирной линией) будет кривой постоянной ширины. Ее углы можно закруглить, воспользовавшись для этого уже описанным ранее способом: продолжить стороны звездчатого многоугольника на одно и то же расстояние
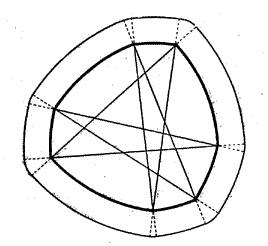
в обе стороны и соединить концы продолженных отрезков дугами окружностей с центрами в вершинах звезды. Кривая с закругленными вершинами, проведенная на рис. 6 тонкой линией, будет другой кривой постоянной ширины. Еще один метод построения кривых постоянной ширины показан на рис. 7. Проведите любое число пересекающихся прямых, затем, ставя по очереди ножку циркуля во все точки пересечения, соединяйте каждый раз дугой окружности те две прямые, которые пересекаются в выбранной вами точке. Начать можно с любой точки, а затем продолжать вычерчивание кривой, сопрягая очередную дугу с предыдущей. Если вы провели все дуги достаточно аккуратно, кривая должна замкнуться, и вы получите еще одну разновидность кривых постоянной ширины. (Доказательство того, что кривая действительно должна замкнуться и быть кривой постоянной ширины, мы оставляем читателю в качестве интересного, но нетрудного упражнения.) Все построенные нами до сих пор кривые постоянной ширины были образованы дугами окружностей лишь двух различных радиусов, но с тем же успехом можно было бы строить кривые постоянной ширины из дуг любого наперед заданного числа окружностей. Более того, кривая постоянной ширины может вообще не состоять из дуг окружности. В самом деле, возьмем квадрат и проведем произвольную кривую, соединяющую его верхнее основание с нижним и касающуюся левой стороны (кривая AВС на рис. 7 справа).
Эта кривая будет левой частью некоторой однозначно определенной кривой постоянной ширины. Чтобы построить недостающую правую часть, проведем множество прямых, каждая из которых параллельна одной из касательных к дуге AВС и отстоит от нее на расстояние, равное длине стороны квадрата. Построить такие прямые нетрудно, если воспользоваться обеими сторонами линейки (исходный квадрат следует выбирать таких размеров, чтобы его сторона была равна ширине линейки). Наложив линейку так, чтобы одна из ее сторон касалась дуги АВС, проведите прямую вдоль ее другой стороны. Проделайте эту операцию в как можно большем числе точек дуги AВС. Огибающая к проведенным прямым и будет недостающей правой частью кривой постоянной ширины. Этот способ позволяет строить неограниченное число «кривобоких» кривых постоянной ширины. Необходимо заметить, что дуга AВС не вполне произвольна. Грубо говоря, ее кривизна ни в одной точке не должна быть меньше кривизны окружности, радиус которой равен стороне квадрата. Дуга AВС не может, например, включать в себя отрезок прямой. Если у вас есть нужные инструменты и вы умеете резать по дереву, вам будет приятно выточить деревянные катки, имеющие в сечении вид различных кривых постоянной ширины. Большинство людей теряют дар речи при виде толстой книги, которая движется на кривобоких катках строго параллельно поверхности стола, не испытывая никакой качки вверх и вниз. Еще проще демонстрировать необычайные свойства кривых постоянной ширины, если вырезать их из картона и прибить к деревянной планке на некотором расстоянии друг от друга. Кривые могут быть самой различной формы, важно лишь, чтобы гвозди проходили через их «центры». Если взять большую, но легкую картонную коробку, поставить ее на вертикально стоящие картонные кривые, прибитые к планке, и покатать вперед и назад, то вы увидите поразительную картину: оба конца планки совершают вертикальные перемещения, а коробка едет на картонных «колесах» так, как если бы они были круглыми! Свойства кривых постоянной ширины. Одно из удивительных и трудно доказываемых
свойств
состоит, в том, что все кривые одной и той же постоянной ширины n имеют
одинаковые периметры. Поскольку окружность принадлежит к числу кривых
постоянной ширины, периметр любой кривой постоянной ширины n равен длине
окружности диаметра n, то есть величине Трехмерные
аналоги кривых постоянной ширины называются телами постоянной ширины. Сфера —
не единственное тело, которое может вращаться внутри куба, все время, касаясь
всех шести его граней. Этим же свойством обладают все тела постоянной ширины.
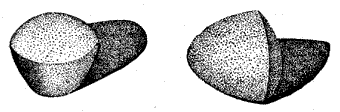
Простейшим примером несферического тела постоянной ширины может служить тело,
образующееся при вращении треугольника Рело вокруг одной из его осей симметрии
(см. левое тело на рис. 8). Существует бесконечно много и других тел постоянной
ширины. Те из них, которые имеют наименьший объем при данной ширине, получаются
из правильного тетраэдра, так же как треугольник Рело — из равностороннего
треугольника: сначала на каждую грань тетраэдра помещают сферические шапочки, а
затем слегка скругляют ребра. Ребра либо исходят из одной вершины, либо
образуют треугольник. Примером такого искривленного тетраэдра постоянной ширины
может служить тело, изображенное на (рис. 8) справа. Поскольку все кривые
одинаковой постоянной ширины имеют один и тот же периметр, может показаться,
будто и все тела одинаковой постоянной ширины имеют одну и ту же площадь
поверхности. Однако такое утверждение не верно. Как показал известный математик
Герман Минковский, все тени, отбрасываемые телами постоянной ширины
(предполагается, что лучи солнца параллельны, а тень падает на плоскость,
перпендикулярную лучам), имеют форму кривых постоянной ширины. Периметры всех
теней, отбрасываемых телами одной и той же постоянной ширины, одинаковы (и
равны
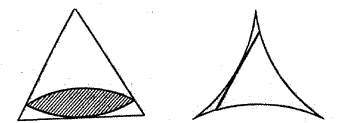
ческие трудности не позволяют изготовлять сверла в форме ротора для равностороннего треугольника, но сверла, позволяющие делать отверстия в форме правильных пяти-, шести и даже восьмиугольников с незакругленными углами, имеются. Доказано, что в трехмерном пространстве существуют несферические роторы для правильного тетраэдра, октаэдра и куба, но не для додекаэдра и икосаэдра. Относительно роторов в пространствах большего числа измерений почти ничего не известно. Непосредственное отношение к теории роторов имеет знаменитая задача об игле, названная в честь сформулировавшего ее еще в 1917 году японского математика Какейя «проблемой Какейя». Заключается она в следующем: в какой плоской фигуре, имеющей минимальную площадь, можно повернуть на 360° единичный отрезок прямой? Такой отрезок, очевидно, можно повернуть на 360° внутри окружности диаметром 1, но ограничиваемый ею круг не будет иметь минимально возможную площадь. Довольно долго математики считали, что решением проблемы Какейя служит кривая, изображенная на (рис. 9 справа), ее площадь равна половине площади круга. (Эта кривая называется гипоциклоидой. Такую кривую описывает точка окружности, катящейся без скольжения внутри большей окружности, если диаметр меньшей окружности составляет 1/3 или 2/3 диаметра большей.) Отломив кусок спички нужных размеров, вы на опыте убедитесь в том, что ее можно повернуть внутри гипоциклоиды как некий одномерный ротор. Обратите внимание, что концы спички будут все время оставаться на контуре гипоциклоиды. Сенсация произошла в 1927 году, через десять лет после того, как Какейя поставил свою проблему. «Виновником» ее стал А. С. Безикович. Он доказал, что проблема Какейя... не имеет решения! Точнее, из результатов Безиковича следовало, что не существует кривой с минимальной площадью, внутри которой единичный отрезок можно было бы повернуть на 360°. Сколь бы малой ни была площадь фигуры, всегда можно построить другую фигуру с еще меньшей площадью, внутри которой единичный отрезок также сумеет развернуться на 360°. Представим себе отрезок, простирающийся от Земли до Луны. По теореме Безиковича, его можно повернуть на 360° внутри фигуры, площадь которой меньше площади почтовой марки с изображением Линкольна. Если и этого вам покажется мало, то тот же отрезок можно повернуть на 360° внутри фигуры, площадь которой меньше площади, занимаемой на почтовой марке носом Линкольна.
Литература: 1. Александров А.Д., Нецветаева Н.Ю. Геометрия. М:,1990. 2. Атанасян Л.С., Базылев В.Т. Геометрия, ч. 1, М:, Просвещение 1986. 3. Данцер Л., Грбнбаум Б., теорема Хелли.- М.: Мир,1968. 4. Моденов П.С. Аналитическая геометрия. М.: 1969. 5. Энциклопедический словарь юного математика/Сост. А.П. Савин.- М.: Педагогика,1985. 6. Математическая энциклопедия: Гл. ред. И.М. Виноградов.- М,: «Советская энциклопедия», 1984. 7. Бляшке В. Круг и шар.- М.: Мир, 1968. |
|||||||||||||||||||||||||||||||||||||||||||||


 Выпуклыми фигурами являются: треугольник,
параллелограмм, трапеция, круг, эллипс (рис.1).
Выпуклыми фигурами являются: треугольник,
параллелограмм, трапеция, круг, эллипс (рис.1).