Дипломная работа: Активізація пізнавальної діяльності учнів в процесі навчання математики

Задача 5. Розвиток малого підприємництва в нашій державі набуває все більшого значення. Побудуйте стовпчасту діаграму динаміки зростання чисельності суб’єктів малого підприємництва та їх доходів в Україні за даними таблиці 2.17.

Ці данн показують, що в Україні створені можливості для підприємницької діяльності, як громадяни використовують для отримання та збільшення власного доходу.

Таблиця 2.17

Динаміка чисельності та доходів суб’єктів малого підприємництва в Україні

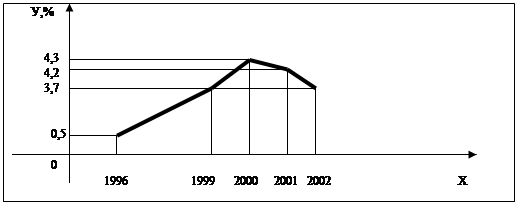
За даними цієї ж таблиці при вивченні теми "Графіки функцій" у дев’ятому клас доцільно з учнями побудувати графік зміни середнього доходу суб’єктів підприємницької діяльності в Україні та провести його аналіз як з математично так і з фінансової сторони. Демонстрація даних таблиці можлива за допомогою кодоскопа.

Розв’язування таких завдань показує учням можливості створення та розширення власного бізнесу, реалізації особистих планів та програм, отримання доходів та покращення добробуту.

В структур грошових доходів родини суттєвим є отримання доходів за рахунок соціальних гарантій.

Соціальн гарантії надаються в межах соціального захисту інтересів населення. Рівень соціальних гарантій та соціальної допомоги залежить від соціальної політики держави. Він спрямований на підвищення добробуту населення та задоволення мінімально необхідних стандартів життєвого рівня населення. Видами та формами соціального забезпечення населення є соціальні допомоги на випадок безробіття, захворювання чи нещасного випадку на виробництві.

Для аналізу робочої спроможності та доходів громадян в Україні завжди відстежується офіційний рівень безробіття

Вивчаючи, тему Графіки функцій” у дев’ятому класі учням можна запропонувати проаналізувати графік (мал. 2.13) “Рівень безробіття в Україні” та відповісти на питання:

Мал. 2.13. Графік рівня безробіття в Україні

1.         Що вибрано за незалежну змінну, а що - за функцію?

2.         В якому році рівень безробіття був найбільшим?

3.         Як змінювалась кількість безробітних з 1996 до 2001 року?

4.         В який період рівень безробіття зростав? спадав?

5.         Яка область визначення функції?

6.         Яка область значень функції?

Робота з такими даними знайомить учнів з фактами впливу на рівень безробіття: науково-технічний прогрес; втілення в життя новітніх технологій, що заміняють живу працю; міграція працездатних осіб, які шукають можливості більше заробляти тощо.

Також до соціальних гарантій відносяться пенсії, стипендії та надання соціально допомоги у разі необхідності.

При подальшій роботі з математичними задачами фінансового змісту про сімейний бюджет було звернуто увагу учнів на наявність різних видів соціальних гарантій, які також джерелом стабілізації доходів родини.

У держав проводиться політика адресного надання соціальної допомоги. До категорій населення, які отримують адресну соціальну допомогу, належать сім’ї з дітьми, віком до трьох років, багатодітні сім’ї, малозабезпечені одинокі громадяни, учасники бойових дій, інваліди війни, особи, які мають особливі заслуги перед Батьківщиною, учасники ліквідації аварії на Чорнобильській АЕС, особи, як мають статус громадян, які постраждали в наслідок Чорнобильської катастрофи та нші.

Крім адресно соціальної допомоги, в Україні діє низка програм, соціально спрямованих на покращення добробуту населення. Однією з них є програма житлових субсидій. Вона захищає сім'ї з низьким рівнем доходів від підвищення цін на житло, комунальн послуги, електроенергію, газ тощо. У зв’язку з цим учням було запропоновано такі задачі:

Задача 8. У Київській області для відшкодування витрат на оплату житлово-комунальних послуг виділено 10 000 тис. грн., а кількість сімей, яким призначено субсидії, становить 200 тис. Який відсоток річного прибутку має кожна з цих родин від користування субсидіями, якщо середньомісячний прибуток кожної родини становить 450 гривень?

Безкоштовн послуги населенню на освіту, охорону здоров'я тощо, є додатковим джерелом надходжень до бюджету сім'ї з бюджетів різних рівнів.

Аналіз різних джерел доходів родини розвиває в учнів фінансовий досвід, вміння застосовувати математичні закони для розрахунку власних грошей. Це показує, що рівень життя громадян залежить від їх діяльності. Напрошується висновок: чим більше в державі заможніх людей, тим багатшою є держава в цілому. Тому потрібно акцентувати увагу учнів на тому, що від особистої діяльності кожного з них як громадянина України залежить як фінансовий стан родини, так і загальний економічний розвиток держави.

Розглянемо як можна ознайомити учнів із статтями витрат сімейного бюджету на уроках математики.

У результат ознайомлення учнів із різними доходами та видатками родини узагальнюючим завданням виступає складання бюджету родини. Доречно запропонувати в дев‘ятому класі під час вивчення теми “Елементи прикладної математики” учням заповнити дома таблицю 2.20.

Таблиця 2.20

Сімейний бюджет

На наступному уроці, під час перевірки домашнього завдання, слід проаналізувати результати з’ясувати відповіді на такі запитання:

1. Як обчислюється відсоток доходів, який припадає на заробітну плату та на інші статті доходів?

2. Чим відрізняється обчислення доходів родини від обчислення видатків?

3. Коли можна вважати, що бюджет родини дефіцитний (видатки більші за доходи)? Профіцітний (доходи більші за видатки)? Збалансований?

4. Яким чином можна розпорядитись залишком коштів, якщо бюджет профіцитний? Як поповнити доходи, якщо бюджет дефіцитний?

5. Якого виду бюджету краще всього дотримуватись у родині, у державі в цілому?

Потім учням було роздано зведений бюджет України за 2003 рік та проведено аналіз наведених даних. Учням пропонувалося ввести свої пропозиції щодо покращення Державного бюджету.

Така робота навчає учнів робити аналіз числових даних та привчає їх корисно розпоряджатися власними коштами та державними коштами.

Ознайомлення учнів з елементами складання бюджету сприяє розумінню фінансових операцій родини, підприємства, фірми та держави в цілому. Учні навчаються ширше бачити можливості застосування власних математичних знань як в повсякденному житті, так і в науковому використанні математичного аналізу різних даних. Це привча робити правильні висновки та прогнозувати подальші власні дії в різних життєвих ситуаціях.

Система задач на сімейний бюджет, яка відображена в додатку Г. Ці задачі сприяють поступовому ознайомленню учнів основної школи з різними фінансовими термінами та поняттями, які важливі для складання розумного сімейного бюджету родини.

2.5. Задачі на страхування та їх особливості

Формування в Україні ринкової економіки та створення різних механізмів ринкових операцій загострює проблеми збереження власних коштів. Зростання ризику у всіх сферах людського життя та господарської діяльності обумовлене необхідністю захисту громадян від можливих витрат та збитків.

Страхування в умовах ринкової економіки ґрунтується на попередньому створенні страхових фондів зі страхових внесків та на відшкодуванні збитків потерпілим. Кожна людина повинна знати, як вона може зменшити свій ризик і скільки їй це коштуватиме. Отже, страхування – це спосіб захисту майнових інтересів громадян в умовах ринкової економіки.

У курс математики основної школи не можливо висвітлити всі особливості страхово справи, оскільки основні засади страхування пов’язані, в першу чергу, з економічним ризиком, який ґрунтується на поняттях теорії ймовірності. Розділ теорії ймовірності сьогодні не включено до програми основної школи, хоча деяк його засади розкриваються учням лише в старшій школі. Тому ознайомлення з усіма математичними розрахунками страхування в основній школі неможливе, але основн поняття та розрахунки страхування як напрямку фінансової сфери людсько діяльності, можуть бути відображені в задачах основної школи.

Страхування як система економічних відносин передбачає наявність двох суб’єктів – страховика та страхувальника. Страховик – це юридична особа (наприклад, акціонерне товариство), яка має право на здійснення страхової діяльності. Страхувальник це особа, яка страхує власне майно або власні інтереси, сплачує страхові внески та має право на отримання компенсації при настанні страхового випадку.

Законом України Про страхування” [41] визначено, що об'єктами страхування можуть бути майнові інтереси, що не суперечать законодавству України. Вони пов'язані з:

·           життям, здоров'ям, працездатністю та додатковою пенсією страхувальника або застрахованої особи (особисте страхування);

·           володінням, користуванням і розпорядженням майна (майнове страхування);

·           відшкодуванням страхувальником заподіяної ним шкоди особі або її майну, а також шкоди, заподіяної юридичній особі (страхування відповідальності).

Відповідно розрізняють страхування добровільне та обов’язкове. Добровільне страхування - це страхування, яке здійснюється на основі договору між страхувальником страховиком. Загальні умови і порядок здійснення добровільного страхування визначаються правилами страхування, що встановлюються страховиком самостійно. Видами добровільного страхування можуть бути: страхування життя; страхування від нещасних випадків; медичне страхування; страхування транспорту; страхування вантажів та багажу; страхування на випадок пожежі та стихійних явищ; страхування майна; страхування кредитів тощо. В Україні здійснюються так види обов'язкового страхування: медичне страхування; особисте страхування медичних працівників на випадок інфікування вірусом імунодефіциту людини при виконанні ними службових обов'язків; особисте страхування працівників пожежно охорони; страхування спортсменів вищих категорій; страхування життя і здоров'я спеціалістів ветеринарної медицини; особисте страхування від нещасних випадків на транспорті; страхування засобів водного транспорту; страхування врожаю; страхування цивільної відповідальності оператора ядерної установки за ядерну шкоду, яка може бути заподіяна внаслідок ядерного інциденту; страхування працівників, які беруть участь у наданні психіатричної допомоги; страхування тварин; страхування відповідальності суб'єктів туристичної діяльності; страхування відповідальності морського судновласника тощо.

Ознайомлення учнів із різними видами страхування та деякими їх особливостями може бути здійснене за допомогою навчальних математичних задач. Розглянемо, наприклад, такі задачі.

Задача 1. Визначити, яке страхове відшкодування отримає сільськогосподарський виробник, якщо він застрахує урожай за таких умов, що страхова компанія відшкодує збитки у розмірі 70% від недоотримання урожаю. Середня врожайність з 1га - 23 ц, а фактично отримали 20 ц з га. Площа посіву 200га. Закупівельна ціна пшениці за 1 ц дорівнює 50 грн.

Для розв’язання цієї задачі потрібно відповісти на запитання:

1.         Якою повинна бути ціна врожаю?

23 × 200 × 50 = 230 000 (грн.)

2.         Яка фактична ціна отриманого урожаю?

20 × 200 × 50 = 200 000 (грн.)

3.         Яка величина збитків?

230 000 – 200 000 = 30 000 (грн.)

4.         Яке страхове відшкодування?

30 000 × 0,7 = 21 000 (грн.)

Відповідь: 21 000 гривень.

Для слабких учнів можуть бути роздані картки де складений план розв’язування задачі. Сильніші учні самостійно складають план та розв’язують задачу.

Робота з такою задачею не лише вчить учнів обчислювати відсотки від певної фінансової суми, а й показує важливість страхування в реальних умовах життя.

В систем страхування застосовують кілька видів фінансових розрахунків та франшизи.

Для визначення величини страхового внеску в страховій практиці часто використовується страховий тариф, який визначається як ставка страхового внеску з одиниці страхово суми за визначений період страхування.

Задача 6. Страховий внесок за майно становив 300 грн. при страховому тарифі 0,2 %. Яка страхова сума застрахованого майна?

Для розв’язання цієї задачі важливо усвідомити, що страховий тариф показує відсоткове відношення між страховим внеском і страховою сумою, тобто 300 грн. є 0,2 % від страхової суми. Тому знаходження страхової суми полягає у знаходження числа за його частиною:

300 : 0,002 = 150 000 (грн.)

Відповідь: 150 000 грн.

У страхуванн майна найпоширенішим є страхування за дійсною вартістю майна, що визначається на день укладання договору. В цьому випадку страхове забезпечення дорівнює величині збитків, тобто повне покриття збитків страхувальника. Для відображення цього виду страхування під час вивчення теми Функція” учням може бути запропоновано задати функціональну залежність між збитками та страховим відшкодуванням і побудувати відповідний графік функції, якщо збитки дорівнюють а грн.

Це завдання не викликає труднощів, але показує механізм фінансових розрахунків у цій ситуації.

Наступний вид розрахунків – страхування за системою пропорційної відповідності. Воно передбачає виплату страхового відшкодування, яке розраховується за формулою 2.10:

, (2.10)

де Q страхове відшкодування ,

S - страхова сума за угодою (страховий внесок),

T вартісна оцінка об’єкта страхування,

W фактична сума збитків.

Це дуже поширений вид страхування. Учням пропонується з формули 2.10 знайти вирази, за яким обчислюється страхова сума за угодою, фактична сума збитків та вартісна оцінка об’єкта страхування. Це знайомить учнів із головними величинами страхової справи та показує математичні залежності між ними.

У 9 класі учням під час вивчення теми “Нерівності” можна запропонувати завдання, яке демонстру використання наведеної вище формули. Наведемо приклад.

Задача 2. Визначити, на яку суму варто застрахувати майно, якщо вартісна оцінка квартири становить 12 000 умовних одиниць, можлива сума збитків 10 000 у. о., а страхове відшкодування повинно бути більше за 8 000 у. о.

Розв’язування цієї задачі можна оформити таким чином.

Складаємо на основі формули 2.10 нерівність:

12 000 × (S/10 000) > 8 000.

Звідси маємо:

S/10 000 > 2/3;

S > 6 666,(6).

Відповідь: бажано застрахувати більше, ніж на 6667 у. о.

В ході аналізу отриманого результату учні спостерігають залежність: покриття збитків тим вище, чим менше різниця між вартісною оцінкою об’єкта страхування та страховою сумою.

Наступний вид – страхування за системою першого ризику. В цьому випадку відбувається виплата відшкодування у розмірі збитків, але в межах страхової суми.

На етап ознайомлення учнів із задачею, важливо пояснити, що під “першим ризиком” у страховій справі розуміють ризик, вартісна оцінка якого не перевищу страхової суми. При дії даної системи страхування, всі збитки у межах страхово суми відшкодовуються повністю. Збитки, які перевищують страхову суму (другий ризик), страховиком не відшкодовуються. Тому розв’язання цієї задачі полягає у виконанні наступної дії: 321 500 – 234 000 = 87 500 (грн.)

У страховій справі особиста участь страхувальника у покритті збитків виражається через франшизу. Франшиза - частина збитків, що не відшкодовується страховиком згідно з договором страхування, тобто це звільнення страховика від покриття збитків на певну суму. Вона може бути встановлена у відсотках або в абсолютних розмірах щодо страхової суми, вартісної оцінки об’єкту або розміру збитків.

Розрізняють умовну та безумовну франшизи. Умовна франшиза звільняє страховика від відповідальності за збитки, які не перевищують встановленої франшизи зобов’язує його покривати збитки повністю, якщо розмір їх перевищує франшизу.

Безумовна франшиза звільняє страховика від компенсації перших х % страхової суми, незалежно від величини збитків. За будь-яких умов вона вилучається з зобов’язань страховика, тому вона безумовна. В цьому випадку страхове відшкодування завжди дорівнює різниці між збитками та безумовною франшизою.

Під час вивчення теми “Функції та їх властивості” учням пропонується задати функцію та побудувати їх графік за такими даними задачі:

Задача 4. Задати функціональну залежність між збитками та страховим відшкодуванням, зробити порівняльний аналіз отриманих результатів, якщо:

1.         Страхова сума становить 200 тис. грн., а умовна франшиза становить 20% від страхової суми.

2.         Страхова сума становить 200 тис. грн., а безумовна франшиза становить 20% від страхової суми.

Міркування над даними задачі проводить до наступних результатів.

Нехай х – сума збитків, а у(х) – страхове відшкодування. В умові задачі франшиза становить 200 000 × 0,2 = 40 000 (грн.)

1.         У випадку умовної франшизи повинні виконуватись умови:

·           якщо величина збитків менше за 40000 грн., то страхове відшкодування дорівнює 0, тобто у = 0;

·           якщо величина збитків більше за 40000 грн., то страхове відшкодування дорівнює сум збитків, тобто у = х.

Врахування цих даних, приводить до такої функції:

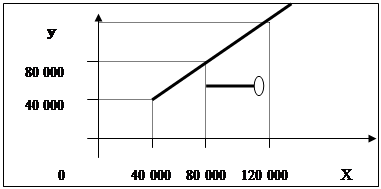
В отримано функції область визначення та область значення лише додатні числа, тому графік функції розташований лише в першій чверті координатної площини. Враховуючи все вище зазначене, отримаємо графік, який зображений на малюнку 2.14.

Мал.2.14. Графік страхових відшкодувань у випадку умовної франшизи

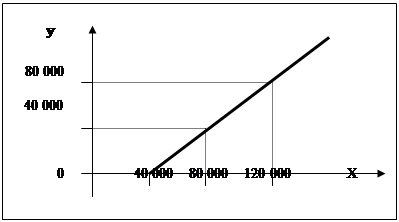
2.         У випадку безумовної франшизи страхове відшкодування завжди дорівню різниці між збитками та безумовною франшизою, тобто .(мал.2.15)

Мал.2.15. Графік страхових відшкодувань у випадку безумовної франшизи

У отримано функції область визначення та область значення лише додатні числа, тому графік функції розташований лише в перший чверті координатної площини (мал.2.15.)

Проводячи порівняльний аналіз отриманих графіків, треба звернути увагу учнів на відмінності, які виникли з особливостей кожного виду франшизи.

Надалі, учням пропонується самостійно задати числові характеристики для різних видів страхування та побудувати графіки функціональної залежності між збитками страховим відшкодуванням за цими умовами.

Для узагальнення дій різних видів страхування учням можуть бути запропоновані задачі, де відбувається страхування за декількома видами.

Задача 5. Обчислити страхові відшкодування за викрадений автомобіль вартістю 8200 грн., якщо він був застрахований у трьох різних компаніях на умовах: в першій - на суму 6 500 грн. за безумовною франшизою у розмірі 5 %, в другій - на суму 8 000 грн. за безумовною франшизою у розмірі 3 %, а в третій - на суму 8 100 грн. за умовною франшизою у розмірі 8 %.

В цьому приклад важливо звернути увагу учнів на те, що у випадку страхування в декількох місцях франшиза обчислюється від відсоткової вартості застрахованого об’єкта, яка попадає на даний договір страхування. Тому обчислення будуть відбуватись за такою схемою:

1.         Загальна страхова сума становить: 6 500+8 000+8 100 = 22 600 (грн.)

2.         Відповідно частки страховиків від загальної суми становлять:

(6 500 : 22 600) × 100 » 28,76 % – для першого,

(8 000 : 22 600) × 100 » 35,40 % – для другого,

(8 100 : 22 600) × 100 » 85,84 % – для третього.

3.         Страхов виплати з врахуванням франшизи становлять:

8 200 × (0,2876 - 0,05) = 1 948,32 (грн.) – для першого,

8 200 × (0,3540 - 0,03) = 2 656,8 (грн.) - для другого,

8 200 × (0,8584 - 0,08) = 6 382,88 (грн.) - для третього.

Відповідь: 1 948,32 грн., 2 656,8 грн., 6 382,88 грн.

Робота з такими даними показує учням особливості, які відбуваються при розрахунках у випадку одночасного страхування одного об’єкта в декількох місцях на різних умовах.

Таким чином, розв’язуючи математичні задачі на страхування учні усвідомлюють такі фінансов поняття, як:

·           страхове відшкодування - страхова виплата, яка здійснюється страховиком у межах страхової суми за договорами майнового страхування і страхування відповідальності при настанні страхового випадку;

·           страхова сума - грошова сума, в межах якої страховик відповідно до умов страхування, зобов'язаний провести виплату при настанні страхового випадку;

·           страховий внесок сума, яка сплачується страхувальником за страхування;

·           страховий тариф - ставка страхового внеску з одиниці страхової суми за визначений період страхування або відношення страхового внеску до страхової суми об’єкту страхування;

·           вартісна оцінка об’єкта страхування;

·           фактична сума збитків;

·           умовна та безумовна франшиза;

·           нші.

Особливост роботи з задачами на страхування в курсі математики основної школи полягають у трактуванні різних страхових термінів в ході розв’язування задач. Тод показується математична залежність в страховій системі. Учні вчаться застосовувати математичні знання у звичайних страхових ситуаціях, які відбуваються в повсякденному житті. Важливість страхової справи в умовах ринкової економіки підкреслюється та розкривається змістом математичних задач на страхування, як ми пропонуємо ввести в курс основної школи (додаток Д). Через систему задач на страхування в курсі математики основної школи відбувається ознайомлення учнів з різними страховими поняттями (додаток Є). Задачі на страхування в курс математики основної школи відображають можливий соціально-фінансовий напрямок захисту власних інтересів кожного громадянина українського суспільства.

2.6. Організація, проведення та аналіз результатів педагогічного експерименту

Основн теоретичні положення активізації пізнавальної діяльності при роботі з математичними задачами фінансового змісту, які висвітлені в роботі, були реалізовані під час проведення експериментального дослідження у шевченківській загальноосвітній школі. Для уточнення активізації пізнавальної діяльності було використано дослідження пізнавального інтересу учнів 9-А класу (14 учнів), його формування та розвиток, що виступає головним показником в процесі пізнавально діяльності учнів.

Робота проводилась з вересня 2006 по травень 2007 р.

Мета експерименту полягала в перевірці робочої гіпотези дослідження. Її перевірка вимагала, в першу чергу, виявлення ефективності впливу запропонованої системи задач на активізацію навчання та формування пізнавального інтересу до математики. В ході експерименту з‘ясовувались доступність та ефективність системи математичних задач фінансового змісту, яка спрямована на формування та розвиток пізнавального інтересу до математики, можливість використання різних прийомів і методів роботи з ними, роль запропонованих задач в процесі навчання математики та в процесі розширення фінансово-математичної обізнаності учнів.

Під час розв‘язання проблеми та перевірки гіпотези розв‘язувались як основні, так часткові завдання. Зокрема:

1.         З‘ясувати спрямованість інтересів учнів 9 класів до учбових предметів та місце математики серед них.

2.         З‘ясувати особливості пізнавального інтересу до математичних задач фінансового змісту.

3.         Визначити методи та засоби роботи з математичними задачами фінансового змісту, що сприяють формуванню та розвитку пізнавального інтересу учнів.

Дослідження проводилось протягом трьох етапів.

На першому етапі була сформульована робоча гіпотеза, визначались конкретні задач дослідження та розроблявся план дослідної роботи. На початковому етап дослідження особлива увага приділялась розгляду та вивченню літератури, аналізу психологічних, педагогічних та методичних праць з даної проблеми та розробц тестів, метою яких було виявлення пізнавального інтересу учнів до математичних задач фінансового змісту та математики в цілому.

На другому етапі проводився пошуковий педагогічний експеримент. В ході експерименту здійснювалась цілеспрямована робота з активізації пізнавальної діяльності учнів при розв’язуванні математичних задач фінансового змісту на уроках математики. В процесі відстежувались зміни у ставленнях учнів до математики та їх успішності. За допомогою різних методик досліджувались рівні пізнавального інтересу учнів.

На третьому етапі за допомогою тестів та анкет проводилось опитування учнів з метою порівняння даних в експериментальних та контрольних класах. Метою опитування було виявлення впливу спеціально підібраної системи математичних задач фінансового змісту та методики її використання на розвиток пізнавального інтересу учнів до математики.

Остаточна робота полягала в обробці, перевірці та уточненні даних, отриманих у процес експерименту, формулюванні висновків.

 Спостереження на уроках математики проводились за планом, який включав: аналіз використання математичних задач фінансового змісту та методів роботи з ними; спостереження за уважністю, самостійністю в теоретичній та практичній діяльності учнів; виявлення інтересу до вивчення математичних основ та, особливо, до роботи із запропонованими задачами.

У процес спостереження зверталась увага на питання, які ставлять учні до вчителів та товаришів, відповіді за власним бажанням, зацікавленість у роботі з математичними задачами фінансового змісту, прагнення зрозуміти життєве значення та застосування даних задач та прагнення поповнювати свої знання самостійно шляхом розв‘язування задач з додаткових джерел.

На початку експерименту за допомогою тестів було з‘ясоване питання про наявність та предметну спрямованість інтересів учнів, а також рівень їх сформованості.

Перший тест включав у себе завдання, де крім вибору відповіді на питання, в деяких випадках, потрібно ще й обґрунтувати свій вибір. (див. Додаток Ж.)

Серед професій, які вказували учні у відповідях на перше питання, зустрічалися такі як бухгалтер, фінансист, економіст, менеджер. Це свідчить про зацікавленість учнів у фінансових операціях та підтверджує ідею необхідності збільшення фінансово освіти в школі.

У відповідях на друге питання, на жаль мало хто з учнів знайшов реальне застосування власних математичних знань. Багато відповідей вказували на те, що учні не знаходять життєвого значення для математики: для допомоги виконувати домашні завдання молодшому брату, для отримання гарної оцінки тощо. Аналіз відповідей на наступні питання тесту подано у таблиці 2.21.

Таблиця 2.21

Аналіз тесту на виявлення рівня пізнавального інтересу до математичних задач фінансового змісту та рівня знань фінансово-математичних операцій і законів

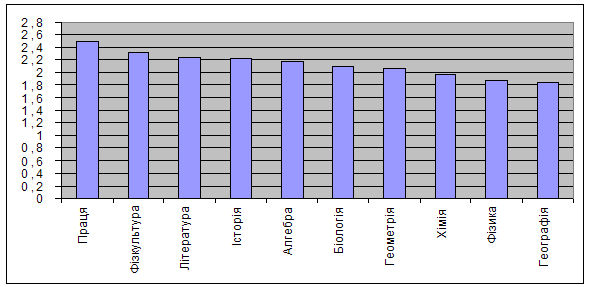
Данні таблиц показують, що у більшості учнів виникає інтерес до фінансової тематики, але програмою основної школи не передбачено ознайомлення учнів з цим напрямком життя. Тому для забезпечення первинних знань фінансових операцій, термінів, законів, ознайомлення з елементарними поняттями фінансового світу доцільно до задач, які розглядаються на уроках математики, включити математичні задач фінансового змісту.

Другий тест було побудовано за селективним методом, який потребував вибору однієї або декількох альтернатив із множини запропонованих (див. додаток З).

З метою виявлення предметної спрямованості інтересів учнів, було запропоновано перше завдання в тесті: "Виписати предмети, які Ви вивчаєте в стовпчик та напроти кожного поставити відповідне число: 3 – якщо Ви любите предмет; 2 якщо предмет Вам подобається; 1 - якщо Ви ставитись до нього байдуже; 0 – якщо Вам предмет зовсім не подобається." Обчисливши середній бал, отримали данні діаграми, які відображені на мал. 2.16.

Як видно з діаграми, алгебра займає п’яте місце серед шкільних предметів,

Мал. 2.16. Середній бал інтересу учнів до навчальних предметів

На запитання "Чим Вам подобається математика?" учні відповідали:

·           своїм науковим змістом, багато важливих та цікавих знань – 26 %;

·           тим, як веде урок вчитель – 37 %;

·           задачами, які ми розглядаємо –22 %;

·           легко вивчати та цікаво виконувати домашнє завдання – 14 % ;

·           математика допомагає мені в житті – 1 %.

На запитання "Що не подобається в математиці?" були такі відповіді:

·           не бачу застосування знань у житті, необхідності у вивченні -23 %;

·           багато не розумію, важко вчити -17 %;

·           не подобаються задачі, які ми розглядаємо - 13 %;

·           на уроках нецікаво - 27 %;

·           багато домашнього завдання - 20 % .

Цікавими виявились відповіді і на запитання: "Чим подобається займатися на уроках математики?". Тут учні назвали:

·           слухати викладача – 23 %;

·           розв‘язувати задачі та завдання разом із класом - 41 % ;

·           самостійно розв‘язувати задачі та працювати з підручником –14 % ;

·           виконувати самостійні та контрольні роботи – 13 %;

·           займатися зайвими справами, які не пов‘язані з математикою – 9 %.

Ці данн вказують на відсутність інтересу до математики, бо коли існує інтерес, то завдання виконуються легко та із задоволенням. Тоді учні використовують додаткову літературу, розв’язують нестандартні завдання і прагнуть до самостійного поширення знань, вмінь та навичок. Певним чином це позначилось і у відповідях на запитання "Які завдання подобається виконувати з математики?". Розподіл був такий:

·           13 % - легкі;

·           25 % - які потребують не дуже складних міркувань;

·           6 % - важкі, підвищеної складності;

·           11 % - на кмітливість та уважність;

·           45 % - пов‘язані з реальним життям.

Аналіз відповідей учнів на це питання ще раз підтверджує, що для підвищення інтересу учнів до вивчення математики необхідно в курс математики основної школи вводити задачі пов‘язані з життєвою реальністю, а не задачі, які не знаходять відображення у повсякденному житті.

Аналіз тестів дав можливість простежити рівень пізнавального інтересу учнів до вивчення математики та фінансових законів через певний проміжок часу. Підсумковий тест проводився в експериментальному класі на кінець проведення експерименту.

Підсумковий тест (див. додаток І) виявлення рівня інтересу учнів до математики та до розв‘язування математичних задач фінансового змісту показав, що в експериментальному класі математика вже стала займати третю позицію щодо інтересу учнів до шкільних предметів, а задач з фінансовим змістом серед всіх навчальних задач зайняли третє місце, після задач пов’язаних із життям та задач - жартів.

У процес дослідження було проведено аналіз підручників з математики, за якими відбувається навчання в основній школі, на наявність в них математичних задач фінансового змісту. Були отримані данні наведені в табл.2.22.

За результатами таблиці 2.22 можна зробити такі висновки:

·           кількість математичних задач фінансового змісту дуже обмежена в шкільному курс математики, серед них зустрічаються комерційні задачі на сімейний бюджет, банківські розрахунки, але зовсім відсутні задачі на податки та цінні папери;

·           кількість математичних задач фінансового змісту трохи збільшується при вивченні теми Елементи прикладної математики” в 9-ому класі, але майже всі вони стосуються складних відсотків нарахування грошей, але діти майже зовсім не ознайомлюються з математичними операціями, які використовуються в фінансових розрахунках;

·           рідко використовуються задачі з недостачею даних, із зайвими даними, не наводяться приклади математичних задач фінансового змісту із заданими даними у вигляд таблиць, графіків, діаграм;

·           відсутн задачі для самостійного фінансового обрахування життєвих даних, що знижує показ реальності математичних операцій та законів;

·           мала кількість математичних задач фінансового змісту, а при викладанні нового матеріалу їх відсутність, знижує інтерес учнів до вивчення абстрактних математичних понять та предмету математика в цілому.

Таблиця 2.22

Математичні задачі фінансового змісту в діючих підручниках з математики

Головне місце в ході дослідження займав експеримент, який включав у себе використання математичних задач фінансового змісту в процесі вивчення математики та різних методів роботи над ними. Це дало змогу виявити особливості пізнавального інтересу учнів до математичних задач фінансового змісту та організувати експериментальне навчання, яке проводилось у звичайних умовах без змін ходу учбового процесу, у відповідності до програм навчання математики.

Під час проведення формуючого експерименту ставилась задача комплексного використання математичних задач фінансового змісту різних видів з метою активізац пізнавальної діяльності учнів та розвитку пізнавального інтересу учнів до вивчення математики та перевірки гіпотези, яка була сформульована в результат спостережень та теоретичного аналізу проблеми.

Експериментальне навчання проводилось в окремому класі у відповідності з чинною програмою. Вивчення матеріалу відбувалось за діючими підручниками, проте робота була посилена по використанню математичних задач фінансового змісту та певних методів роботи з ними, що сприяло підвищенню інтересу учнів до вивчення математики та, в загальному, активізувало пізнавальну діяльність учнів.

Задачний матеріал було розроблено та розподілено майже за всіма темами, що вивчаються в курсі математики основної школи. Він відповідав зазначеним вимогам до змісту задач та методиці їх використання. Час для роботи над задачами даної групи з‘являвся за рахунок заміни типових задач підручника математичними задачами фінансового змісту. Крім того, велика кількість задач обговорювалась на уроці, а подальша робота виносилась на самостійне дослідження.

Результати експерименту показали, що використання задач фінансово-економічного змісту при вивченні математики в середній школі сприяє підвищенню інтересу учнів до математики та підвищенню їх успішності.

ВИСНОВКИ

Результати проведеного теоретичного дослідження та педагогічного експерименту дозволяють нам сформулювати висновки щодо їх практичного використання:

1.         Активізація пізнавальної діяльності учнів – це перехід до більш високого рівня активност та самостійності учнів у процесі навчання, який стимулюється розвитком пізнавального інтересу, та відбувається завдяки удосконаленню методів та прийомів навчального процесу.

2.         Показниками та ознаками прояву активності та інтересу учнів у процесі роботи над задачею є:

·           постановка запитань;

·           відстеження помилок в процесі роботи над задачею;

·           використання отриманих раніше знань;

·           прагнення розв’язувати нестандартні задачі;

·           пошук цікавих математичних фактів, використання набутих математичних знань у повсякденному житті;

·           самостійне створення задач;

·           допомога одноліткам у розв’язанні складніших завдань;

·           пошук альтернативних способів розв’язування задач тощо.

3.         Розв’язування математичних задач фінансового змісту та введення їх в учбову програму основно школи сприяє створенню необхідного емоційного настрою, активності учнів у навчанні та розширенню сфери практичного застосування вмінь та навичок учнів, отриманих у процесі вивчення математики.

4. Математичн прикладні задачі фінансового змісту виконують:

·           освітню функцію, оскільки їх використання спрямоване на формування у школярів системи знань, вмінь та навичок на різних етапах навчання;

·           розвиваючу функцію, бо робота з ними розвиває вміння осмислювати зміст понять, застосувати здобуті знання на практиці, аналізувати результати, робити відповідн узагальнення, порівняння та висновки;

·           виховну функцію, бо економічне та фінансове виховання на уроках математики може здійснюватися насамперед завдяки цим задачам;

·           контролюючу функцію як навчальні задачі.

5. Для досягнення активізац пізнавальної діяльності учнів при роботі з математичними задачами фінансового змісту потрібно дотримуватись виконання таких вимог до задач:

·           задача повинна бути правильно подана (вчитель пояснює важливість її розв‘язання для подальшої роботи та набуття відповідних вмінь);

·           задача повинна бути зрозуміла учням, тобто пояснені всі терміни, які зустрічаються в задачі, ситуація описана в задачі відома та цікава для учнів із життєво необхідності, вимога задачі повинна викликати інтерес;

·           задача повинна бути посильною учням, тобто учні повинні мати досвід роботи з такими задачами або можуть самостійно набути необхідних знань;

·           задача повинна викликати інтерес завдяки хоч одній умові: зовні цікавого формулювання, незвичної постановки запитання чи процесу розв’язування задачі;

·           задача повинна розвивати життєвий досвід учнів, показувати можливість використання шкільних знань у різних життєвих ситуаціях.

6. Система математичних задач фінансового змісту виступає ефективним засобом активізац пізнавальної діяльності учнів основної школи. Це відбувається на основ підвищення пізнавального інтересу учнів, досягається акцентуванням уваги на значенні знань в реальному житті та реалізується вибором методів, форм засобів навчання.

7.  Використання учителями математичних задач фінансового змісту потребує певної їх підготовки, а запропонована система задач можливе бути введена в курс математики основно школи завдяки заміні учбових задач та завдань із “застарілою” фабулою новими задачами фінансового змісту.

8.  Результати експериментальної перевірки та досвід впровадження системи математичних задач фінансового змісту в практику основної школи підтверджують правильність висунутої гіпотези. Зокрема, вони свідчать про її позитивний вплив на весь навчально-виховний процес, а саме: використання системи математичних задач фінансового змісту сприяє:

·          формуванню пізнавального інтересу учнів до вивчення математики;

·          підвищенню успішності та якості математичної підготовки учнів;

·          формуванню в учнів знань, вмінь та навичок використання математичних знань у фінансовій сфері людської діяльності;

·          розвитку логічного мислення, творчої активності та пізнавальної самостійності школярів.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1.         Ананьев Б.Г. Психология и проблемы человекознания : Избранные психологические труды. – М.: Изд-во Моск. псих.- соц. ин-та, 1996. – 384 с.

2.         Аристова Л.П. Активность учения школьника. - М.: Просвещение, 1968. - 210 с.

3.         Бабанский Ю.К. Проблемное обучение как средство повышения эффективности учения школьников. - Ростов- на-Дону: 1970. - 31 с.

4.         Бевз Г.П. Алгебра: Підручник для 7-9 кл. серед. шк. - К.: Освіта, 2003. - 303 с.

5.          Бевз Г.П. Методика викладання математики. - К.: Вища школа, 1989. - 376 с.

6.          Бевз Г.П. Методика розв'язування алгебраїчних задач у 6-8 класах. Посібник для вчителя. - К.: Рад. шк., 1975. - 204 с.

7.         Брушлинський А.В. Психология мышления и проблемного обучения. – М.: Знания, 1983. – 96 с.

8.         Буряк В.К. Самостоятельная работа учащихся. - М.: Просвещение, 1984. - 64с.

9.         Виготский Л.С. Собрание сочинений: В 6-ти томах. – М.: Педагогика, 1982. – Т.4 Детская психология / Под ред. Д.Б. Эльконина. – 432 с.

10.       Винокуров Е.Ф. Школьное экономическое образование и учитель математики // Математика в школе. – 2001.- №2. – С.23- 27.

11.       Габай Т. В. Учебная деятельность и ее средства. - М.: МГУ, 1988. - 255 с.

12.       Гнеденко Б.В. Математика и математическо образование в современном мире. - М.: Просвещение, 1985. - 190 с.

13.       Голанд Е.Я. О развитии самостоятельности и творческой активности учащихся в процесе обучения // Воспитание познавательной деятельности и самостоятельности учащихся. Ч.1. – Казань: 1969. – С.78 - 89.

14.       Груденов Я.И. Совершенствование методики роботы учителя математики. - М. : Просвещение, 1990. - 224 с.

15.       Гурова Л.Л. Психологический анализ решения задач. – Воронеж: 1976. – 340 с.

16.       Данилов М.А. Воститание у школьников самостоятельности и творческой активности. – Казань: Тат.кн.изд-во, 1963.- 96 с.

17.      Дубинчук Е.С. Активизация познавательной деятельности учащихся средних професионально-технических училищ в процесе обучения математике. - К.: Вища школа, 1987. - 101 с.

18.       Дутка Г.Я. Практикум з математики для економістів. - Л.: 1998. – 362 с.

19.       Есипов Б.П. Самостоятельная работа учащихся на уроках. - М.: Учпедгиз, 1961. - 239 с.

20.       Закон України “Про банки і банківську діяльність 2121-III від 07.12.2000

21.       Закон України “Про загальну середню освіту” // Освіта. – 1997. 20-27 серпня. – С.6-11.

22.       Закон України “Про оподаткування прибутку підприємств” від 12.08.1994

23.       Закон України “Про освіту” // Голос України. – 1996. – 25 квітня. – С.1-6.

24.      Закон України “Про податок на додану вартість” від 01.10.1997.

25.      Закон України “ Про страхування” від 7.03.1996

26.      Закон України “Про цінні папери і фондову біржу” (1991) Мін.фін. України № 04-305 від 30.09.1991 р.

27.       Зимняя И.А. Педагогическая психология: Учебник для вузов. – М.: Логос, 2001. – 384 с.

28.       Ігнатенко М.Я., Соколенко Л.О. Реалізація прикладної спрямованості шкільного курсу математики як засіб активізації навчально-пізнавальної діяльності учнів. Навчальний посібник. - К.: ІЗМН, 1997. - 76 с.

29.      Кабанова Меллер Е.Н. Формирование приемов умственной деятельности и умственное развитие учащихся. – М.: Просвещение, 1968. – 160 с.

30.      Колягин Ю.М. Задачи в обучении математике. Ч.1.Математические задачи как средство обучения и развития учащихся. - М.: Просвещение, 1977.- 110с.

31.      Колягин Ю.М. Задачи в обучении математике. Ч.2. Обучение математике через задачи и обучение решению задач. - М.: Просвещение, 1977. - 144 с.

32.       Конституція України. К.: Юрінком, 1996. – 80 с.

33.      Кордемский Б.А. Увлечь школьников математикой. - М.: Просвещение, 1981. - 112 с.

34.      Корсакова О.К. Методи навчання, що формують в учнів досвід перетворювальної діяльності. – К.: ФАДА ЛТД, 2000. – 28 с.

35.      Крутецкий В.А. Психология математических способностей школьников. - М.: Просвещение, 1968. - 432 с.

36.      Кудрявцев П.Д. Современная математика и ее преподавание. – М.: Наука, 1980. – 144с.

37.      Левинберг Л.М., Ібрагимов Р.А. Активизация познавательной деятельности младших школьников ( на материале математики). – Ташкент: Из-во “Фан” АН УзССР, 1991. – 216с.

38.      Матушкина З.П. Формирование умений решать задачи при обучении математике учащихся 4-5 классов. Дис… канд. пед. наук.: 13.00.02. - М.,1985. - 223 с.

39.      Матюшкин А.М. Проблемные ситуации в мышлении и обучении. - М.: Педагогика, 1972. - 208 с.

40.      Махмутов М.И. Организация проблемного обучения в школе. – М.: Просвещение, 1977. – 240с.

41.      Менчинская Н.А. Задачи в обучении / В кн. Педагогическая энциклопедия. Т.2 - М.: Просвещение, 1965. - С.3-16.

42.      Педагогічний словник / за ред. М.Д. Ярмаченка - К.: Пед. думка, 2001. - 516 с.

43.      Пидкасистый П.И. Самостоятельная деятельность учащихся. – М.: Педагогика, 1972. – 184 с.

44.      Податкова система України / За ред. Федосеева В.М. – К.: Либідь,1994. – 464 с.

45.      Пономарев Я.А. Психология творения: Избр. псих. труды – Воронеж: Модэк, 1999. – 480 с.

46.      Пономаренко О.І. Сучасний фінансовий аналіз і фінансові числення // У світі математики. - 1997. - т.3. в.1.– С. 28-42.

47.      Про затвердження інструкції “Про прибутковий податок з громадян.”// Все про бухгалтерський облік. - № 67 (492) від 24.07.2000. – С.12 – 38.

48.      Про податки і збори населенню України: Посібник / М.Я. Азаров, Г.І. Бондаренко, П.В. Мельник та інші – Ірпінь: Академія ДПС України, 2000. – 182 с.

49.      Психологические основы формирования личности в педагогическом процессе / Под ред. А. Коссановски, Х. Кюка, И. Ломпшер, Г. Розенфелда. Перевод с немецкого. – М.: Педагогика, 1981. 224 с.

50.      Ростовецкая Л.А. Самостоятельность личности в познании и общении. – Ростов-на-Дону: РГПИ, 1975. – 297с.

51.      Рубинштейн С.Л. Основы общей психологии. – М.: Педагогика, 1989. – 320с.

52.      Cкаткин М.Н. Совершенствование процесса обучения. Проблемы и суждения. – М.: Педагогика, 1971. – 206 с.

53.      Скрипченко О.В., Лисянська Т.М., Скрипченко Л.О. Довідник з педагогіки та психології. – К.: Видавництво Національного педагогічного університету імені М.П. Драгоманова, 2002. – 216 с.

54.      Cрода Г.В. Воспитание активности и самостоятельности учащихся в обучении. – М.: Изд-во АПН РСФСР, 1956. – 56 с.

55.      Статистичний збірник України за 2000 рік. - К.:, 2001. – 432 с.

56.      Фридман Л.М. Учитесь учиться математике: Кн. для учащихся. – М.: Просвещение, 1985. – с.112.

57.      Фридман Л.М. Логико-психологический анализ школьных учебных задач. – М.: Педагогика, 1977. – 208 с.

58.      Фридман Л.М., Кулагина И.Ю. Психологический справочник учителя. – М.:Просвещение, 1991. – 288с.

59.      Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи. – М.: Просвещение, 1984. – 175 с.

60.      Харламов И.Ф. Педагогика в вопросах и ответах. – М.: Гардарики, 2001. – 253 с.

61.      Харламов И.Ф. Педагогика. Минск: Універсітэцкае, 2000. – 560 с.

62.      Шамова Т.И. Активизация учения школьников. –М.: Педагогика, 1982 – 208 с.

63.      Шапиро И.М. Использование задач с практическим содержанием в преподавании математики. - М.: Просвещение, 1990. - 96 с.

64.      Шорох-Троцький С.Н. Методика арифметики для учителей начальных школ. – М.,1915. – 78 с.

65.      Щукина Г.И. Актуальные вопросы формирования интереса в обучении. – М.: Просвещение, 1984. 176 с.

66.      Щукина Г.И. Педагогические проблемы формирования познавательных интересов учащихся. – М.: Педагогика, 1988. – 203 с.

67.      Якиманская И.С. Знания и мышление школьника.– М.: Знание, 1985. – 78с.

68.      Якиманская И.С. Личностно ориентированное обучение в современной школе. – М.,1996. –96 с.