|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Дипломная работа: Економічна модель оптимізації закупівель та поставок кондитерських виробів на прикладі товариства з обмеженою відповідальністю "Гермес-Груп"Математична модель цієї задачі має вигляд: Визначити такі перемінні х1 і х2, що задовольняють наступним умовам c1x1+c2x2= b, (2.1.6) x1 ≥ 0, x2 ≥ 0 (2.1.7) при
яких функція Як правило, функція (2.1.7) може мати довільний нелінійний вид. Використовуючи класичні методи оптимізації, варто чітко уявляти собі розходження між локальним екстремумом функції, глобальним екстремумом і умовним екстремумом. При цьому корисно повторити визначення локального і глобального екстремумів для функц однієї перемінної. Поняття умовного екстремуму вводиться для випадку, коли число перемінних n не менше 2 (n≥2). Будемо
думати, що функція Точка Х*, у якій усі частки похідні функції z = f (X) рівні 0, називається стаціонарною точкою. Необхідна умова екстремуму. Якщо в точці Х* функція z = f (X) має екстремум, то частки похідні функції в цій точці рані нулеві:
Отже, точки екстремуму функції z = f (X) задовольняють системі рівнянь (1.5.5):
Як
у випадку одна перемінної, необхідне умова не є достатнім для того, щоб
стаціонарна точка була точкою екстремуму. Для одержання достатніх умов варто
визначити в стаціонарній точці знак диференціала другого порядку. Диференціал
другого порядку позначається d2 f (x1, x2,…,xn)
дорівнює сумі добутків часток похідних другого порядку на відповідні збільшення
аргументів. Якщо від частинної похідної
Достатн умови екстремуму: а)
у стаціонарній точці X0 функція 6)
якщо в)
якщо Для
функції двох перемінних Знайдемо значення часток похідних другого порядку в стаціонарній точці Х0(х01,х02):
(можна переконатися, що а12 = а21). Позначимо через ∆ визначник, складений з аij для i, j = 1,2:
Тод достатні умови екстремуму функції двох перемінних мають вигляд: а) якщо ∆ > 0 і а11 < 0 (а22 < 0), те в точц Х0 функція має максимум: якщо ∆ > 0 і а11 > 0 (а22 > 0), те в точці Х0 — мінімум (у цих випадках Х0 = Х '); б) якщо ? < 0, те екстремуму немає; в) якщо ∆ = 0, то питання про екстремум залишається відкритим. Схема визначення екстремуму функції n перемінних збігається з правилами визначення локального екстремуму функції однієї перемінної. Умовний екстремум. Нехай
необхідно знайти екстремум функції
Передбачається, що функції f і φi, мають безперервні частки похідні по всім перемінним. Рівняння (2.1.9) називають рівняннями зв'язку. Говорять,
що в точці Х0 = Легко помітити, що задача визначення умовного екстремуму збігається з задачею нелінійного програмування (2.1.4), (2.1.5). Один
зі способів визначення умовного екстремуму застосовується в тому випадку, якщо
з рівнянь зв'язку (2.1.9) n перемінних, наприклад
Підставивши
отримані вираження для
Задача
зведена до перебування локального (глобального) екстремуму для функції (2.1.11)
від n-m перемінних. Якщо в точці Х0 = Метод множників Лагранжа Інший спосіб визначення умовного екстремуму починається з побудови допоміжної функц Лагранжа, що в області припустимих рішень досягає максимуму для тих же значень перемінних х1, х2,..., хn, що і цільова функція z. Нехай
вирішується задача визначення умовного екстремуму функції Складемо функцію, що називається функцією Лагранжа.
де
Легко
помітити, що
Задача опуклого програмування (ОП) Нехай дана система нерівностей виду функція
причому
усі функції Усяка задача лінійного програмування є часткою случаємо задачі опуклого програмування (ОП). У загальному випадку задачі ОП є задачами нелінійного програмування. Виділення задач ОП у спеціальний клас порозумівається екстремальними властивостями опуклих функцій: усякий локальний мінімум опуклої функції (локальний максимум увігнутої функції) є одночасно і глобальним; крім того, задана на замкнутій обмеженій безлічі, досягає на цій безлічі глобального максимуму і глобального мінімуму. Звідси випливає, що якщо цільова функція Z є строго опуклою (строго увігнутої) і якщо область рішень системи обмежень не порожня й обмежена, то задача ОП завжди має єдине рішення. У цьому випадку мінімум опуклої (максимум увігнутої) функції досягається усередині області рішень, якщо там мається стаціонарна точка, або на границі цієї області, якщо усередині неї нема стаціонарної точки. (У загальному випадку можна затверджувати лише, що безліч оптимальних рішень будь-якої задачі ОП є опуклою безліччю). Наближене рішення задач опуклого програмування методом кусочно-лінійної апроксимації Функція
(не виключено, що Fi(xi) = 0 при деяких i). Нехай
у задачі ОП (2.1.15), (2.1.16) і функція мети Z, і всі обмеження
Ідея
методу кусочно-лінійної апроксимації полягає в тому, що всі fi,
всі Для побудови наближеної задачі розглянемо кусочно-лінійну апроксимацію функц одному перемінної h(х), заданої на відрізку [0, а]. Розіб'ємо цей відрізок на r частин точками х0 < х1 <...< хr так, щоб х0 = 0, хr = а (малюнок 2.1.1).
Рисунок 2.1.1 – Кусочно-лінійна апроксимація функції однієї перемінної Обчислимо значення функції hk(x), у цих точках. З'єднаємо попарно точки (хk; hk) і (хk+1; hk+1) відрізками прямих. Складена з цих відрізків ламана h(х) апроксимує функцію h(х) на відрізку [0, а]. (Не розглядаючи тут оцінку точності наближення, відзначимо тільки, що точність можна збільшити за рахунок більш дрібної розбивки відрізка). Рівняння
ділянки ламаної
(рівняння
прямої по двох точках). Якщо кожне з відносин у цій рівності позначити через причому
Відзначимо,
що для кожного
де (Рівняння (2.1.20) називаються параметричними рівняннями відрізка. Якщо h(x)=0, те друге з цих рівнянь звертається в тотожність 0 = 0. Таким
чином, для будь-якого
причому
завжди відмінні від нуля тільки два значення Повертаючи
до задачі ОП із сепарабельними функціями, відзначимо, що насамперед (у
залежності від системи обмежень) потрібно визначити інтервал зміни кожно
перемінної хj. Потім кожен цей інтервал розбивається на частин
точками хjk і з використанням формул (2.1.21) будується
кусочно-лінійна апроксимація для функцій fj і знайти максимум функції
при обмеженнях
Оскільки
наближена задача (2.1.22) є задачею лінійного програмування і ми звичайно
вирішуємо її симплексним методом, умови незаперечності перемінних записуються
окремо від інших обмежень. Відмінність отриманої задачі (2.1.22) від звичайно
задачі лінійного програмування полягає в тому, що для кожного xj мається
не більш двох сусідніх ненульових 2.2 Дослідження об’ємів закупівель та продажів В даному підпункті необхідно дослідити стан закупівель та продажів підприємства, обчислити недоотриману виручку від реалізації за минулий рік, обчислити відсоток втрат по кожному виробу кожного підприємства. Зробити висновки щодо подальшої політики діяльності фірми. ТОВ «Гермес-Груп» відповідно до статуту займається оптовою торгівлею продуктами харчування. В основному, це кондитерські вироби. Головними постачальниками є: київська кондитерська фабрика «Київград», ТМ «Росічі», ТМ «Кремінь», ТМ «Буринь», Київський кондитерський завод з виробництва пряників. Проведений фінансовий аналіз показав, що підприємство у 2008 році було неплатоспроможним. Активи підприємства були ліквідними, загрози попасти в тяжкий фінансовий стан не було. Але розрахований коефіцієнт обертання дебіторської заборгованості показав, що гроші за відвантажений товар перераховуються не вчасно, тому підприємство не може правильно скоригувати свою діяльність, свої об'єми закупівель. Кожна гривня обєму реалізації приносить 3.5 % прибутку за рік в цілому. Багато показників вказують на те, що підприємство неефективно використовує свої активи для отримання прибутку. Підприємство спочатку закуповувало товар на підприємствах-виробниках, а потім продавало його підприємствам- споживачам. Розрахунки з постачальниками були після доставки товарів одразу. А розрахунки зі споживачами проводилися невчасно. Внаслідок цього підприємство мало багато поверненого, неоплаченого товару, тобто мало збитки. Необхідно порівняти усі об’єми продажів та закупівель у 2008 році та розрахувати втрати виробництва. Втрати обчислюються як різниця між закупівлями та продажами. Відсоток втрат по одному виробу обчислюється за формулою 2.2.1:
Відсоток втрат повинен бути не більше 9-10%. Збільшення цього відсотку свідчить про те, що підприємство працює в збиток собі. Закупівля та продаж кондитерських виробів ООО «Гермес-Груп» у 2008 році складали об’єми, які приведені в зведеній таблиц 2.2.1. Таблиця 2.2.1 – Об’єми продажів та закупівель у 2008 році
В таблиці 2.2.1 показано, що від невірно сформованих закупівель ООО «Гермес-Груп» втрачає 10654 кг кондитерських виробів за рік. І недоотримує за рік 97554,60 грн. Тобто частину цих 10654 кг воно змушене повертати заводам-виробникам, частину продавати з великими знижками або робити розпродаж з ціллю отримання прибутку. Розглянемо рисунки 2.2.1, 2.2.2, 2.2.3, 2.2.4, 2.2.5 на яких зображені відсотки втрат кожного кондитерського виробу від загальних втрат.
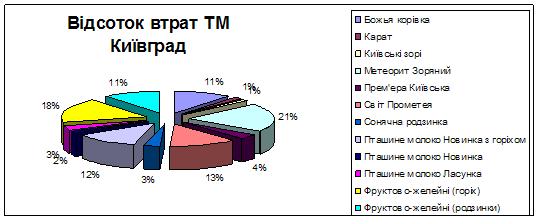
Рисунок 2.2.1 – Відсоток втрат ТМ Київград З рисунка 2.2.1 легко помітити, що необхідно приділити увагу закупівлі таких видів продукції, як Метеорит Зоряний (21 %), Фруктово-желейні (горіх) (18 %), Світ прометея (13 %), Пташине молоко Новинка з горіхом (12%).
Рисунок 2.2.2 – Відсоток втрат ТМ Росичі З рисунка 2.2.1 видно, що практично ні один з видів кондитерських виробів не вигідно закуповувати. Тобто політику роботи з цією торгівельною маркою треба передивитися та прийняти заходи по підвищенню продажів виробів ТМ Росичі.
Рисунок 2.2.3 - Відсоток втрат ТМ Кремінь З рисунка 2.2.3 легко помітити, що з маркою Кремінь працювати досить вигідно. Не варто закуповувати лише цукерки Злагода. Вони складають 31 % втрат в загальному.
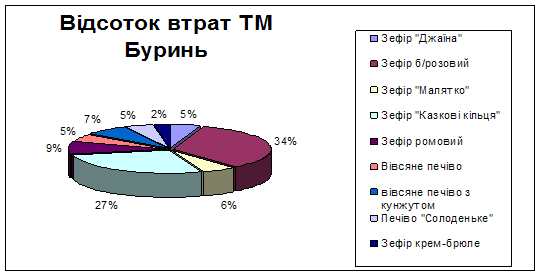
Рисунок 2.2.4 – Відсоток втрат ТМ Буринь Рисунок 2.2.4 вказує на те, що підприємству необхідно приділити увагу закупівлям виробів: зефір Зефір б/рожевий (34%), Зефір Казкові кільця (27%).
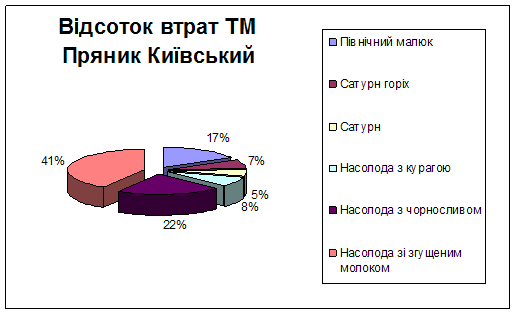
Рисунок 2.2.5 – Відсоток втрат ТМ Пряник Київський На роботу з цією маркою необхідно привернути увагу. Більша кількість виробів має великий відсоток втрат. Відсотки втрат дуже великі, тому необхідно запропонувати такі умови, які б підвисили б об’єми продажів на підприємстві з мінімальними втратами. З проведеного аналізу закупівель та продажів видно, що підприємство мало б отримати від продажу кондитерських виробів за рік на 97000 гривень більше, аніж отримало. З проведеного аналізу рентабельності продажів видно, що кожна гривня об’єму реалізації приносить 0% прибутку за перший квартал, 5.5 % за 9 місяців діяльності підприємства, 3.5 % за рік в цілому. З проведених досліджень видно, що необхідно скласти таку модель оптимізації, яка б максимізувала прибуток підприємства та виражала б найкращі умови і для виробників, і для споживачів. На величину прибутку впливають обсяги закупівель та продажів. Шляхом підвищення прибутку буде визначення оптимального обсягу закупівель та продажів на підприємстві при гнучкій системі цін. 2.3 Постановка задач оптимізації закупівель Підхід до побудови математичної моделі може бути індуктивним і дедуктивним. При використанні індуктивного методу модель того чи іншого економічного процесу будується за допомогою часткового моделювання, що охоплює більш прості змінн економічного процесу, з переходом від них до загальної моделі всього процесу. При дедуктивному методі спочатку будується загальна модель і лише на її основ конструюються часткові моделі, встановлюються алгоритми конкретних математичних розрахунків. Економіко-математичні моделі будуть найбільш обґрунтованими, якщо при їхньому конструюванні методи індукції і дедукції використані в єдності. У цих умовах забезпечується більша «подібність» моделі на реальний економічний процес; вона в більшій мірі буде відображати об'єктивно існуючі економічн явища і закономірності[4]. При проведенні досліджень було виявлено, що підприємство веде неправильну політику при вирішенні обсягів закупівл товарів на заводах-виробниках. Також результати опитань та досліджень показали, що на ринку продажу кондитерських виробів існує висока конкуренція. Тому споживачів необхідно заохочувати пільгами та вигідними пропозиціями при купівл кондитерських виробів. При підвищенні обсягів закупівель продукції споживачами вигідно знизити ціни, щоб збільшити обсяг закупівель у виробників і тим самим збільшити обсяг продажу виробів. Іноді вигідно знизити ціни, щоб збільшити об’єми продажів. Для заохочення споживачів необхідно створити таку систему цін продажів товару, яка б залежала від обсягу закупівель з боку споживачів. Необхідно розробити економіко-математичну модель, яка б розраховувала максимальний прибуток при оптимальному обсяз закупівель. Завод і випускає та прода продукцію j в об’ємі x. Підприємство закупає цю продукцію в об’ємі х та продає її в об’ємі у. Шляхом аналізу необхідно поставити головну умову розробки економіко-математичної моделі: процес закупівлі попереджається замовленням необхідних обсягів на підприємствах-виробниках. В подальшому викладенні ці замовлення-закупівлі будемо називати закупівлями. x = y або обсяг закупівель дорівнює обсягу продажів. Тобто для досягнення максимального прибутку на підприємстві необхідно прийняти таку умову – закупівлі підприємства повинні дорівнювати продажам споживачам. Розробимо таку систему цін, щоб задовольнити потреби споживачів. Побудуємо графік залежності обсягу закуповано продукції від цін (рисунок 2.3.1).
Рисунок 2.3.1 – Графік залежності обсягу продажів від ціни На рисунку 2.3.1 y – обсяг закупованої продукції; x – ціна. З вище наведеного графіка легко побачити, що при закупівлі продукції в об’ємі y1 ціна ц закупівлі буде максимальна – х4, а при максимальному обсяз закупівлі у4 ціна буде мінімальною – х1. Тобто підприємство закуповує кондитерськ
вироби за цінами Відпускна ціна i-го заводу, j-ї продукц
( Відпускна ціна залежить від обсягів
закупівель, тобто Така залежність знаходиться по статистичним даним як рівняння регресії: |
|

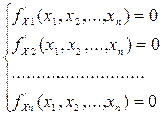 (2.1.8)
(2.1.8)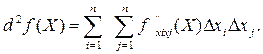
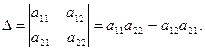
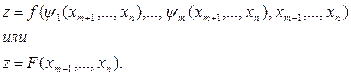 (2.1.11)
(2.1.11) (2.1.13)
(2.1.13)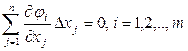 (2.1.14)
(2.1.14)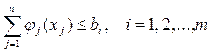 (2.1.18).
(2.1.18).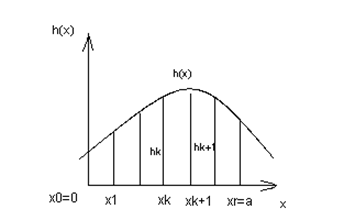

 (2.1.19)
(2.1.19)  (2.1.20)
(2.1.20)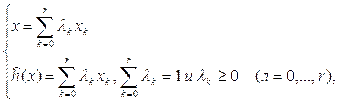 (2.1.21)
(2.1.21)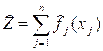
 (2.1.22)
(2.1.22)