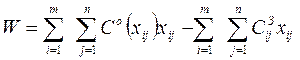|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Дипломная работа: Економічна модель оптимізації закупівель та поставок кондитерських виробів на прикладі товариства з обмеженою відповідальністю "Гермес-Груп"
де a і b – коефіцієнти. Вони знаходяться з рівняння прямої, яка проходить через дві задані точки [].
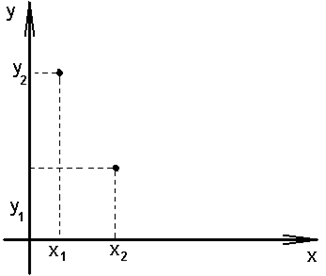
Також їх можна знайти, виходячи з графіка, представленого на рисунку 2.3.2.
Рисунок 2.3.2 - Графік для знаходження рівнянь двох точок
y1 = ax1 + b
b = y1 - ax1, де х1 і х2 – обсяги продажів 1 і 2; у1 і у2 – відпускн ціни при об’ємах закупівель 1 і 2. Прибутком підприємства (W) є різниця між відпускними цінами та закупівельними, які пов’язані з обсягом закупівлі. З вищеоговореного складемо економіко-математичну модель максимізації прибутку (2.3.2).
Підставимо (2.3.1) в (2.3.2), отримаємо (2.3.3) та (2.3.3.а):
Дана функція має ряд обмежень. Підприємства-виробники обмежують ряд закупівель, які повинно замовити підприємство. Обсяги закупівлі xij підприємства обмежен можливостями підприємств-виробників (2.3.4). Цільова функція – параболічна. Залишкова дисперсія в неї нижче аніж у лінійної функції, тому що вона краще описує об’єкт дослідження та моделювання. Але дослідженнями було доказано, що закупівельні ціни – це не всі витрати, які залежать від обсягів закупівель – це тільки частина. Закупівельна ціна містить в собі відсоток втрат. Відсоток втрат встановлюється шляхом дослідження. Таке дослідження може бути застосовано для підприємств оптової торгівлі. Закупівельні ціни можна використовувати як ндикатор втрат, розуміючи під Сз закупівельні ціни плюс втрати. 2.4 Вибір методу оптимізації закупівель Сформульована математична задача може бути вирішена одним з розроблених математичних методів. Методи елементарної математики використовуються в звичайних традиційних економічних розрахунках при обґрунтуванні потреб у ресурсах, обліку витрат на виробництво, розробці планів, проектів, при балансових розрахунках і т.д. Ці методи використовуються не тільки в рамках інших методів, але й окремо. Існу безліч методів рішення поставленої задачі. Розглянемо деякі з тих, за допомогою яких можна вирішити запропоновану модель. Метод покоординатного спуску Цей метод є найбільш простим із прямих методів пошуку мінімуму функції декількох перемінних. Викладемо ідею методу для випадку функції двох перемінних f (x, y). Виберемо початкове наближення M0 (х0, у0). Зафіксуємо в0 і знайдемо мінімум функції однієї перемінної f (x, y0). Нехай він досягається при х = х1. Уздовж прямій, рівнобіжній осі ОХ, здійснюємо спуск у точку Mt (х1, у0). Фіксуємо х1 і знаходимо мінімум функції однієї перемінної f (х1, у). Нехай це буде в1. З точки М1 (х1, у0) рухаємося уздовж прямій, рівнобіжній осі OY, до точки М2 (.x1, у1). Потім знову здійснюємо спуск із точки М2 уздовж прямої рівнобіжної осі ОХ і т.д. (рисунок 2.4.1).
Рисунок 2.4.1 – Метод покоординатного спуска Відомо, що якщо функція f (х, у) має безупинні друг похідні в околиці мінімуму, то при відповідному виборі початкового наближення (х0, у0) спуск по координатах сходиться до мінімуму. Зокрема, метод сходиться, якщо в області D, обмеженою лінією рівня, що проходить через точку М0 {х0, у0), виконуються умови:
Частки похідні функції прагнуть до нуля. Метод сходиться зі швидкістю геометрично прогресії. Метод градієнтного спуску Метод визначення мінімуму функції f(х), х=(x1, x2,..., хп), називаний методом градієнтного чи найшвидшого спуска, запропонованийі Коши. Для мінімізації по методу спуска вибирається початкова точка х0= (х01, х02,..., х0n) (звичайно відповідно до фізичного змісту задачі). Функція f (x) = f (х0) визначає в n-мірному просторі гіперповерхня, градієнт якого вказує напрямок найшвидшого зростання функції. Тому в напрямку — grad f(х0) функція швидше за все убуває при нескінченно малому русі з даної точки. Спуск по цьому напрямку до мінімуму визначає нове наближення х1.. У цій точц знову визначається градієнт здійснюється спуск у напрямку антиградієнта. Випадок п = 2 представлений на рисунку 2.4.2
Малюнок 2.4.2 – Метод градієнтного спуску для n=2 Вектор х, який було необхідно знайти послідовно уточнюється на k-й ітерації методу градієнтного спуска по формулі 2.4.2.
де hk — оптимальний крок для k -й ітерації. Таким чином, на кожнім кроці градієнтного спуска потрібно
вирішувати ще задачу мінімізації функції одним перемінної яким-небудь чисельним
методом. Зокрема, можна розкласти функцію в ряд Тейлора, обмеживши членами
другого порядку, і визначити hk. Однак такий метод приводить до дуже громіздких
обчислень. При цьому необхідно враховувати також трудомісткість обчислення
значень функції f(х) і її градієнта в точках хк. Тому на практиці часто h
вибирають емпіричним шляхом. Здійснюється спуск при довільному hk; якщо
значення функції f (хk+1) зменшиться, те переходимо до наступного кроку спуска,
якщо ж
f (хk+1) не убуває, те зменшуємо крок hk. Варто
враховувати, що якщо hk вибрати дуже малим, те це приводить
до істотного збільшення обсягу обчислень, якщо hk занадто
велике, те це може привести до проскакування через мінімум функції. Обчислення
по формулі (2.4.2) проводимо доти, поки функція f(х) практично перестане
убувати, тобто до виконання для наперед заданого ε нерівності Критерієм закінчення ітераційного процесу пошуку мінімуму можна вибрати також умова:
Метод Ньютона Описаним вище методам властивий один загальний недолік повільна збіжність, якщо поверхні (лінії) рівня мінімізуємої функції витягнуті, сильно відрізняються від сфер (окружностей). У методі Ньютона мінімізац функції декількох перемінних цей недолік усувається обліком значень других похідних, однак застосуємо цей метод для більш вузького класу функцій. Нехай в околиці стаціонарної точки х* функція f (x)= f (х1,..., хп) двічі безупинно дифференцируема і її матриця Гессе
позитивно визначена. Тоді, застосовуючи для рішення системи
(2.4.3) метод Ньютона, або модифікований метод Ньютона, одержимо тераційний процес для мінімізації функції або
Позитивна визначеність матриці Н (х) забезпечу збіжність методу Ньютона до рішення системи (2.2.3), причому збіжність буде квадратичної, а при застосуванні модифікованого методу Ньютона — лінійної. Приведемо на рисунку 2.2.3 блок-схему рішення вищевикладеного методу Ітераційний процес (2.4.4) називають методом Ньютона (модифікованим методом Ньютона) мінімізації функції f(х) п перемінних х = (x1, x2,..., хп). Варто врахувати, що в методі Ньютона на погрішність накладається погрішність звертання матриці H(xk). У зв'язку з цим для функції п перемінних при великому п застосовують модифікований метод Ньютона (2.4.4). Відзначимо, що для квадратичної форми метод Ньютона дає точний результат при першій терації.
|
| Наименование изделия | Закупочная цена, Сз | Отпускная цена Со1 | Отпускная цена Со2 | Объем продаж в кг при Со1 | Объем продаж в кг при Со2 |
| Абрикос с орехом | 30.20 | 33.55 | 33.82 | 100.00 | 10.00 |
| Желейная с орехом (абрикос) | 16.22 | 16.09 | 16.22 | 100.00 | 10.00 |
| Желейная с орехом (слива) | 16.22 | 16.09 | 16.22 | 100.00 | 10.00 |
| Лесовик | 32.95 | 36.61 | 36.90 | 100.00 | 10.00 |
| Праздничный десерт | 26.89 | 26.68 | 26.89 | 100.00 | 10.00 |
| Чернослив с орехом | 26.17 | 29.08 | 29.31 | 100.00 | 10.00 |
| Божья коровка | 14.86 | 15.15 | 15.27 | 260.00 | 100.00 |
| Карат | 23.96 | 24.42 | 24.62 | 260.00 | 100.00 |
| Киевские зори | 29.14 | 29.70 | 29.94 | 260.00 | 100.00 |
| Метеорит звездный | 21.15 | 21.56 | 21.73 | 260.00 | 100.00 |
| Премьера Киевская | 15.43 | 15.73 | 15.86 | 260.00 | 100.00 |
| Свет Прометея | 22.55 | 22.99 | 23.17 | 260.00 | 100.00 |
| Солнечная изюминка | 23.96 | 24.42 | 24.62 | 260.00 | 100.00 |
| Птичье молоко "Новинка с орехом" | 16.08 | 16.39 | 16.52 | 260.00 | 100.00 |
| Птичье молоко "Новинка" | 15.86 | 16.17 | 16.30 | 260.00 | 100.00 |
| Птичье молоко "Лакомка" | 16.08 | 16.39 | 16.52 | 260.00 | 100.00 |
| Фруктово-желейные (орех) | 14.73 | 15.02 | 15.14 | 260.00 | 100.00 |
| Фруктово-желейные (изюм) | 14.73 | 15.02 | 15.14 | 260.00 | 100.00 |
| Злагода | 10.13 | 10.33 | 10.41 | 160.00 | 60.00 |
| Лукум с изюмом | 7.20 | 7.34 | 7.40 | 160.00 | 60.00 |
| Лукум молочный | 6.99 | 7.13 | 7.19 | 160.00 | 60.00 |
| Рахат-лукум цветной | 6.34 | 6.46 | 6.51 | 160.00 | 60.00 |
| Рахат-лукум в кунжуте | 7.10 | 7.24 | 7.30 | 160.00 | 60.00 |
| Весна (мармелад) | 7.87 | 8.02 | 8.09 | 160.00 | 60.00 |
| Нуга орех с кунжутом | 9.87 | 10.06 | 10.14 | 160.00 | 60.00 |
| Нуга "Загадка" | 11.00 | 11.22 | 11.31 | 160.00 | 60.00 |
| Кос-халва "Белоснежка" | 8.74 | 8.91 | 8.98 | 160.00 | 60.00 |
| Шербет арахис. с курагой | 7.74 | 7.89 | 7.95 | 160.00 | 60.00 |
| Шербет восточн.сюрприз | 7.54 | 7.68 | 7.75 | 160.00 | 60.00 |
| Шербет Фараон | 7.56 | 7.70 | 7.77 | 160.00 | 60.00 |
| Шербет арахис. с черносливом | 7.34 | 7.48 | 7.54 | 160.00 | 60.00 |
| Шербет Султан | 7.47 | 7.61 | 7.67 | 160.00 | 60.00 |
| Шербет Самаркандский | 7.54 | 7.68 | 7.75 | 160.00 | 60.00 |
| Шербет Эмир | 7.93 | 8.09 | 8.15 | 160.00 | 60.00 |
| Дайма-ойла шоколад (вост.сладости) | 9.21 | 9.38 | 9.46 | 160.00 | 60.00 |
| Дайма-ойла земфира (вост.сладости) | 9.80 | 9.99 | 10.07 | 160.00 | 60.00 |
| Дайма-ойла шоколадно-фруктовая (вост.сладости) | 9.27 | 9.45 | 9.52 | 160.00 | 60.00 |
| Дайма-ойла Кременчукская (вост.сладости) | 8.44 | 8.60 | 8.67 | 160.00 | 60.00 |
| Зефир "Джаина" | 6.57 | 6.70 | 6.75 | 65.00 | 15.00 |
| Зефир б/розовый | 6.13 | 6.25 | 6.30 | 65.00 | 15.00 |
| Зефир "Малятко" | 6.57 | 6.70 | 6.75 | 65.00 | 15.00 |
| Зефир "Сказочные кольца" | 6.32 | 6.44 | 6.49 | 65.00 | 15.00 |
| Зефир ромовый | 6.29 | 6.41 | 6.46 | 65.00 | 15.00 |
| Овсяное печенье | 4.01 | 4.09 | 4.12 | 65.00 | 15.00 |
| Овсяное печенье с кунжутом | 4.44 | 4.53 | 4.57 | 65.00 | 15.00 |
| Печенье "Сладенькое" | 6.99 | 7.13 | 7.19 | 65.00 | 15.00 |
| Северный малыш | 3.98 | 4.06 | 4.09 | 65.00 | 15.00 |
| Сатурн орех | 4.71 | 4.80 | 4.84 | 65.00 | 15.00 |
| Сатурн | 3.98 | 4.06 | 4.09 | 65.00 | 15.00 |
| Насолода с курагой | 4.82 | 4.91 | 4.95 | 65.00 | 15.00 |
| Насолода с черносливом | 4.82 | 4.91 | 4.95 | 65.00 | 15.00 |
| Насолода со сгущенным молоком | 4.82 | 4.91 | 4.95 | 65.00 | 15.00 |
Розрахуємо коефіцієнти a і b та функцію відпускної ціни за даними таблиці 2.5.1, яка знаходиться в таблиці 2.5.2. Коефіцієнти a і b знаходяться з рівнянь, які отримані з рівняння прямої, яка проходить через дв точки.
![]()
b = y1 - ax1
![]()
Таблиця 2.5.2 – Розрахунок функції відпускної ціни
| Наименование изделия | a | b | Со(х)=ах+в |
| Абрикос с орехом | -0.00298 | 34.06 | 33.82 |
| Желейная с орехом (абрикос) | -0.00143 | 16.26 | 16.22 |
| Желейная с орехом (слива) | -0.00143 | 16.26 | 16.22 |
| Лесовик | -0.00325 | 38.20 | 36.90 |
| Праздничный десерт | -0.00237 | 26.96 | 26.89 |
| Чернослив с орехом | -0.00258 | 29.39 | 29.31 |
| Божья коровка | -0.00076 | 15.29 | 15.27 |
| Карат | -0.00122 | 25.10 | 24.62 |
| Киевские зори | -0.00149 | 30.53 | 29.96 |
| Метеорит звездный | -0.00108 | 22.16 | 21.75 |
| Премьера Киевская | -0.00079 | 15.88 | 15.86 |
| Свет Прометея | -0.00115 | 23.63 | 25.18 |
| Солнечная изюминка | -0.00122 | 25.10 | 24.62 |
| Птичье молоко "Новинка с орехом" | -0.00082 | 16.85 | 16.52 |
| Птичье молоко "Новинка" | -0.00081 | 16.32 | 16.30 |
| Птичье молоко "Лакомка" | -0.00082 | 16.81 | 16.52 |
| Фруктово-желейные (орех) | -0.00075 | 15.16 | 15.14 |
| Фруктово-желейные (изюм) | -0.00075 | 15.16 | 15.14 |
| Злагода | -0.00083 | 10.74 | 10.41 |
| Лукум с изюмом | -0.00059 | 7.42 | 7.40 |
| Лукум молочный | -0.00057 | 7.20 | 7.19 |
| Рахат-лукум цветной | -0.00052 | 6.53 | 6.51 |
| Рахат-лукум в кунжуте | -0.00058 | 7.32 | 7.30 |
| Весна (мармелад) | -0.00064 | 8.15 | 8.09 |
| Нуга орех с кунжутом | -0.00081 | 10.47 | 10.14 |
| Нуга "Загадка" | -0.00090 | 11.67 | 11.31 |
| Кос-халва "Белоснежка" | -0.00071 | 9.27 | 8.98 |
| Шербет арахис. с курагой | -0.00063 | 7.97 | 7.95 |
| Шербет восточн.сюрприз | -0.00061 | 7.76 | 7.75 |
| Шербет Фараон | -0.00062 | 7.78 | 7.77 |
| Шербет арахис. с черносливом | -0.00060 | 7.56 | 7.54 |
| Шербет Султан | -0.00061 | 7.69 | 7.67 |
| Шербет Самаркандский | -0.00061 | 7.76 | 7.75 |
| Шербет Эмир | -0.00065 | 8.41 | 8.15 |
| Дайма-ойла шоколад (вост.сладости) | -0.00075 | 9.76 | 9.46 |
| Дайма-ойла земфира (вост.сладости) | -0.00080 | 10.39 | 10.07 |
| Дайма-ойла шоколадно-фруктовая (вост.сладости) | -0.00076 | 9.82 | 9.52 |
| Дайма-ойла Кременчукская (вост.сладости) | -0.00069 | 8.94 | 8.67 |
| Зефир "Джаина" | -0.00107 | 7.18 | 6.75 |
| Зефир б/розовый | -0.00100 | 6.49 | 6.30 |
| Зефир "Малятко" | -0.00107 | 7.18 | 6.75 |
| Зефир "Сказочные кольца" | -0.00103 | 6.90 | 6.49 |
| Зефир ромовый | -0.00103 | 6.87 | 6.46 |
| Овсяное печенье | -0.00065 | 4.14 | 4.12 |
| Овсяное печенье с кунжутом | -0.00072 | 4.59 | 4.57 |
| Печенье "Сладенькое" | -0.00114 | 7.64 | 7.19 |
| Северный малыш | -0.00065 | 4.161042 | 6.7536 |
| Сатурн орех | -0.000768 | 5.0304 | 6.3 |
| Сатурн | -0.00065 | 4.218798 | 6.7536 |
| Насолода с курагой | -0.000786 | 5.14568 | 6.49152 |
| Насолода с черносливом | -0.000786 | 5.14568 | 6.46128 |
| Насолода со сгущенным молоком | -0.000786 | 5.14568 | 4.12272 |
Дослідженнями було доказано, що закупівельні ціни – це не всі витрати, які залежать від обсягів закупівель – це тільки частина. Закупівельна ціна містить в собі відсоток втрат. Відсоток втрат встановлюється шляхом дослідження. В таблиці 2.5.3 приведемо відсотки втрат, які додаються до закупівельної ціни по кожному з заводів-споживачів.
Таблиця 2.5.3 – Відсоток втрат в закупівельній ціні
| Наименование предприятия | Процент потери |
| Росичи | 12% |
| Киевград | 9% |
| Креминь | 8.50% |
| Бурынь | 9% |
| Пряник Киевский | 9% |
При отриманих даних про коефіцієнти, розрахуємо оптимальний об’єм закупівель та максимальний прибуток підприємства. Результати обчислень представимо в таблиці 2.5.4.

 (2.3.2)
(2.3.2)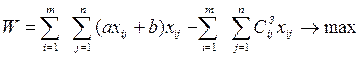 (2.3.3.)
(2.3.3.)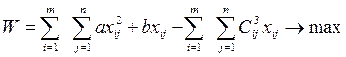 (2.3.3.а)
(2.3.3.а)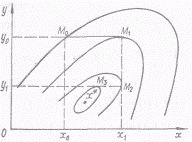
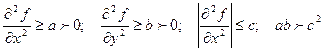 (2.4.1)
(2.4.1)
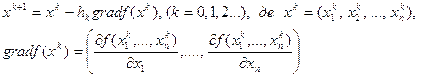 ,
, 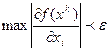

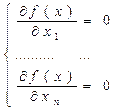
 (2.4.4)
(2.4.4)
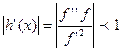 навколо xN. Якщо xN
простим коренем, то виконуються співвідношення f’(xN) ≠ 0 та
h’(xN) = 0. Тобто, для початкового значення х(0) повинна
виконуватися нерівність
навколо xN. Якщо xN
простим коренем, то виконуються співвідношення f’(xN) ≠ 0 та
h’(xN) = 0. Тобто, для початкового значення х(0) повинна
виконуватися нерівність , де (2.4.5.)
, де (2.4.5.)