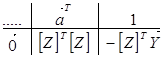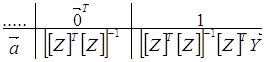|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Курсовая работа: Економіко-математичне моделювання в управлінні підприємством аграрно-промислового комплексуКурсовая работа: Економіко-математичне моделювання в управлінні підприємством аграрно-промислового комплексуЗміст Вступ 1. Економіко-математичне моделювання 1.1 Основні типи моделювання 1.2 Етапи побудови економіко-математичних моделей 1.3 Особливості побудови математично моделі економічного явища чи процесу 1.4 Методи економіко-математичного моделювання 1.4.1 Множинна лінійна регресія. Множинна лінійна регресія в стандартизованому масштабі 1.4.2 Множинна нелінійна регресія 1.4.3 Метод Брандона 1.5 Важливість моделювання для підприємств аграрно-промислового комплексу 1.6 Постановка завдання 2 Аналіз собівартості для планування урожайност сільскогосподарської продукції 2.1 Аналіз собівартості сільськогосподарської продукції 3. Економіко-математичне моделювання в управлінн підприємством 3.1 Економіко-математичне моделювання урожайност сільськогосподарської продукції методом Брандона. 3.2 Комп’ютерна реалізація методу Брандона 3.3 Функціональні можливості програми прогнозування урожайності Висновок Перелік використаної літератури ВступУ останн десятиліття в економічній науці і господарській практиці все ширше застосовується математика. Як основна причина швидкого розповсюдження економіко-математичних методів і моделей перш за все необхідно назвати різке ускладнення сучасної економічної практики, викликане високим рівнем розвитку продуктивних сил, глибокою спеціалізацією виробництва, збільшенням темпів науково-технічного прогресу. Всі ці чинники, доповнені вимогою підвищення ефективності використання природних ресурсів, кількість яких далеко не безмежно, а також необхідність усвідомлення близьких і віддалених екологічних наслідків господарської діяльності людства, приводять до зростання вимог, що пред'являються до якості рішень, що приймаються в народному господарстві. Використання методів економіко-математичного моделювання на базі широкого розповсюдження обчислювальної техніки є одним з найважливіших важелів підвищення якост економічних рішень. Господарська діяльність завжди була пов'язана з необхідністю проведення хоч би найпростіших арифметичних або геометричних розрахунків. Більш того, математика виникла на основі практичних господарських потреб. Тому розрахункова робота близька зрозуміла економістам і господарникам, так що поява електронної обчислювально техніки, яка на перший погляд мало відрізнилася від звичайних арифмометрів (хіба що була більш швидкодіючою) само по собі не могло змінити методів ухвалення господарських рішень: просто традиційні розрахунки, що займали раніше багато годин і днів, стали здійснюватися за секунди. При цьому, поступово зрозуміли, що збільшення швидкості розрахунків на декілька порядків дозволяє вирішувати такі розрахункові завдання, про які раніше і думати було нічого. Так, замість одного варіанту господарського рішення стало можливим оцінити, декілька варіантів. Результати цих розрахунків, представлені господарникові, відповідальному за ухвалення рішення (як прийнято говорити, особі, що ухвалю рішення (ОУР)), дали йому можливість вибрати з розглянутих варіантів рішення найбільш відповідний. В процесі вибору рішення за допомогою обчислювальної техніки на основі оцінки його декількох варіантів і у господарника, і у дослідника виникають наступні питання. Чи проглянути всі цікаві варіанти. рішень? Які міркування покладені в основу оцінки наслідків можливих варіантів рішення? Як сформулювати показники, що характеризують ефективність функціонування системи, щодо якої ухвалюються рішення? Як вибрати найбільш відповідне рішення? Для того, щоб відповісти на ці питання, аналізовану проблему необхідно описати точно. Мовою, найбільш відповідною для цього, є мова математики. Опис системи, що вивчається, на мові математики - це і є її математична модель. Окрім засобів опису, математика надає засоби аналізу моделі, які дозволяють досліджувати властивості і вибрати найбільш відповідне рішення. Таким чином, процес впровадження в економічну практику обчислювальної техніки як засоби обробки нформації неминуче приводить до принципово нового етапу - побудови. математичних моделей економічних об'єктів і їх аналізу. Цим дослідженням, які прийнято називати економіко-математичним моделюванням, присвячена дана робота. 1. Економіко-математичне моделювання1.1 Основні типи моделюванняРозвиток науки тісно пов'язаний з побудовою і використанням різноманітних моделей. Хоча зараз число вже побудованих моделей важко оцінити навіть приблизно, питання про визначення поняття "модель" до цих пір викликає суперечки. Більш того, протягом останніх двох-трьох десятиліть, коли про моделі, стали говорити буквально всі - хіміки і лінгвісти, астрономи і логіки, біологи і економісти, розбіжності в тлумаченні цього терміну ще більш збільшилися. Надалі ми обмежимось тим розумінням слова "модель", яке використовується в широко поширеному методі дослідження, званому моделюванням. Моделювання - це вивчення об'єктів дослідження не безпосередньо, а непрямим шляхом, за допомогою аналізу деяких допоміжних об'єктів, які прийнято називати моделями. Цього визначення дотримуватимемося надалі; воно є загальноприйнятим як в природних науках, так в економічних дослідженнях. Моделювання як спосіб віддзеркалення дійсності зародилося ще в античну епоху одночасно з виникненням наукового пізнання. Зараз важко назвати ту область науки, де б воно не використовувалося. У економічних дослідженнях методи моделювання також грають найважливішу роль. [4] Класифікацію методів моделювання і моделей можна проводити по різних ознаках: по сфер додатку, по характеру модельованих об'єктів, по ступеню подробиці моделей і т.д. Моделі класифікуватимуться по засобах моделювання. Такий вибір пов'язаний з тим, що нас перш за все цікавить можливість використання різних засобів для аналізу економічних систем. По засобах моделювання методи моделювання діляться на дві великі групи: методи матеріального моделювання і методи ідеального моделювання (див. Додаток). Матеріальним моделювання називається у тому випадку, коли дослідження ведеться на моделях, зв'язок яких з досліджуваними об'єктами існує об'єктивно, має матеріальний характер. Моделі в цьому випадку або будуються дослідником, або відбираються їм в навколишньому його світі. У матеріальному моделюванні можна умовно виділити три основні підгрупи методів: просторове, фізичне і аналогове моделювання. У просторовому моделюванні використовуються моделі, призначені для того, щоб відтворити або відобразити просторові властивості об'єкту, що вивчається. Моделі в цьому випадку геометрично подібні до об'єкту дослідження. У якості прикладом такої групи можна назвати макети різноманітних типів. Моделі, використовувані у фізичному моделюванні, призначені для відтворення динаміки процесів, що відбуваються в науковому об'єкті, причому спільність процесів, що відбуваються в об'єкті дослідження і моделі, ґрунтується на схожості їх фізичної природи. Цей метод моделювання, особливо широко поширений в техніці, де фізичне моделювання використовується для проектування технічних систем різного типу. Мабуть, найбільш відомим прикладом використання фізичного моделювання є дослідження літальних апаратів на основі експериментів в аеродинамічній трубі. Третя підгрупа методів матеріального моделювання зв'язана з використанням матеріальних моделей, що мають іншу фізичну природу, але що описуються тими ж математичними співвідношеннями, що і об'єкт, що вивчається. Таке моделювання називається аналоговим і ґрунтується на аналогії в математичному описі моделі і об'єкту. Найбільш простій приклад аналогового моделювання - вивчення механічних коливань за допомогою електричної системи, що описується тими ж диференціальними рівняннями, але зручнішою для проведення експериментів. У всіх випадках матеріального моделювання модель - це матеріальне віддзеркалення початкового об'єкту. Дослідження полягає в матеріальній дії на неї, тобто в експерименті з моделлю. Таким чином, матеріальне моделювання, але своїй природ експериментальним методом. Від матеріального моделювання принципово відрізняється ідеальне моделювання, що ґрунтується не на матеріальній аналогії між моделлю і об'єктом, що вивчається, а на ідеальному, мислимому зв'язку між ними. Методи ідеального моделювання можна (досить умовно) розбити на дві підгрупи: формалізоване і неформалізоване (інтуїтивне) моделювання. У формалізованому моделюванні моделями служать системи знаків або образів, разом з якими задаються правила їх перетворення і інтерпретації. Якщо в якість моделей використовуються системи знаків, то таке моделювання називається знаковим. Знаков системи бувають різними - це можуть бути креслення, графіки, схеми, формули і т.д. Найважливішим видом знакового моделювання є математичне моделювання. При використанні математичного моделювання модель записується у вигляді сукупност формул, перетворення яких здійснюється на основі правил логіки і математики. Роль математичного моделювання як в розвитку науки, так і в практичній діяльності величезна, приклади його застосування добре відомі кожному з шкільних часів. Іншою формою формалізованого моделювання є образне моделювання, в якому моделі будуються з таких наочних елементів, як пружні кулі, потоки рідини, траєкторії руху тіл. Аналіз образних моделей здійснюється в думках і може бути віднесений до формалізованого моделювання у тому випадку, коли правила взаємодії образів, використовуваних в моделі, чітко фіксовані. Наприклад, в ідеальному газ зіткнення двох молекул розглядається як пружне зіткнення куль; при цьому результат зіткнення мислиться усіма однаково. Моделі такого типу широко використовуються у фізиці при проведенні досліджень, які прийнято називати уявними експериментами. Перейдемо до розгляду неформалізованого моделювання. До нього можна віднести такий аналіз проблем різноманітного типу, коли модель не формулюється, а замість не використовується не деяке зафіксоване точне уявне віддзеркалення реальності, що служить основою для міркування і ухвалення рішень. Таким чином, всяке міркування, що не використовує формалізовані моделі, можна (якщо, звичайно, той, що мірку має хоч якесь уявлення про предмет міркування) вважати неформалізованим моделюванням, оскільки в цьому випадку у того, що говорить, пише або мислячого; ндивідуума є деякий образ об'єкту дослідження, який можна інтерпретувати як неформалізовану модель реальності. Дослідження економічних процесів і явищ протягом довгого часу проводилося тільки на основі таких невизначених уявлень, та і в даний час аналіз неформалізованих моделей залишається найбільш поширеним методом економічного дослідження: всяка людина, що ухвалює економічне рішення без використання математичних моделей, вимушена керуватися тим або іншим описом ситуації, заснованим на досвіді (своєму або чужому) і на інтуїції. Основним недоліком такого підходу, є те, що рішення може виявитися малоефективним або навіть помилковим. У буденному житті така помилка може бути допустимою, але при ухваленні економічних рішень крупного масштабу втрати будуть дуже великі. Використання виключно неформалізованого моделювання стримує і розвиток економічної науки, оскільки одна і та ж модель різними дослідниками може розумітися по-різному приводити не тільки до не співпадаючих, але ледве чи по до протилежних виводів. Звичайно, неформалізоване моделювання має і важливі достоїнств, дякуй яким воно залишається (і залишиться в досяжному майбутньому) основним засобом ухвалення рішень у величезній більшості буденних ситуації. Аналіз ситуації на основі досвіду і інтуїції можна проходити швидко, зрозуміло для того, що ухвалює рішення і часто вельми ефективно. Зараз методи математичного моделювання в економіці ще не можуть конкурувати з неформалізованими методами по швидкості, легкості і дешевизн дослідження. Крім того, в багатьох моделях не враховуються важливі чинники, ясні для ОУР, але що погано формалізуються. Тому в даний час ведуться нтенсивні роботи по побудові людино-машинних систем, в яких досвід і інтуїція ОУР доповнюються точним розрахунком на основі математичних моделей. [1] В процес використання перед дослідником неминуче виникає наступна проблема: чому по властивостях моделей можна судити про властивості досліджуваних об'єктів? Загальна відповідь на це питання відсутня: цю проблему доводиться ретельно аналізувати у кожному конкретному випадку, особливо гостро вона стоїть при використанн методів ідеального моделювання. Основною особливістю ідеального моделювання (і формалізованого, і інтуїтивного) є те, що для дослідження, взагалі кажучи, байдуже, яка матеріальна основа вибрана для запису моделі. Одна і та ж модель може бути записана олівцем на папері, крейдою на дошці, реалізована у вигляді програми на обчислювальній машині або лише в думках сформульована дослідником. Часто одні і ті ж операції з моделлю можна проводити і за допомогою олівця або крейди, і за допомогою ЕОМ, і в думках. Таким чином, деякий реальний процес, що є матеріальною основою операцій, що проводяться з моделлю, не має ніякого відношення ні до виводів, зроблених на основі моделі, ні до модельованого об'єкту. Тому ідеальні моделі стоять від об'єкту, що вивчається, значно далі, ніж моделі матеріального моделювання, дослідження яких полягає в матеріальній дії па природні процеси. Дослідження за допомогою ідеальних моделей носять теоретичний характер, оскільки в них дія па модель не пов'язано з дією на природу. Який-небудь об'єктивний матеріальний зв'язок між моделлю і досліджуваним явищем відсутній, тому за допомогою деального (зокрема математичного) моделювання можна легко отримати результати, що не мають ніякого відношення до досліджуваного явища, що робить питання про відповідність моделі об'єкту, що вивчається, центральним питанням ідеального моделювання. [4] Які ж достоїнства методу моделювання примушують постійно удаватися до нього як в наукових дослідженнях, так і в практичній діяльності, не дивлячись на складну проблему оцінки відповідності між моделлю і об'єктом, що вивчається? На це питання можна дати дві відповіді, доповнюючи один одного. Перш за все, використання моделей має чисто практичну основу: моделі завжди будуються так, щоб вони були зручніш для дослідження, чим початкові об'єкти (тобто були простіше, мали зручніш параметри і т.д.). Більш того, деякі явища вдається вивчити тільки на їх моделях. Є, проте, і інша відповідь на питання про роль методів моделювання: у моделях відтворюються лише основні, найбільш важливі в даному дослідженн сторони об'єкту, що вивчається, тому моделювання дозволяє виявити істотн чинники, відповідальні за ті або інші властивості явищ, що вивчаються. У цьому сенсі розвиток методів моделювання визначає розвиток науки і має величезне практичне значення, оскільки достатньо ясне уявлення про властивості процесів в природі і суспільстві служить основою для отримання правильних відповідей на запити практики. Особливо важливу роль має ідеальне моделювання. Розвиток будь-якої науки можна трактувати у вельми загальному, але цілком розумному сенсі як побудова ідеальних моделей. Уміння будувати ідеальні, особливо математичні моделі, достатньо властивості реальних процесів і систем, що точно описують і пояснюючі, служить ознакою зрілост науки. Розглянемо питання про те, якою мірою методи моделювання можуть бути використані для аналізу економічних процесів. Почнемо з матеріального моделювання. Геометричні форми різних економічних об'єктів - далеко не головна характеристика економічних систем, так що методи просторового моделювання при аналізі економічних процесів широкого розповсюдження отримати не змогли. Цікавіше питання про такий метод матеріального моделювання, який був би близький по ідеї до фізичного моделювання, широко використовуваного в природних науках і техніці. Модель об'єкту, що вивчається, в цьому випадку повинна мати ту ж матеріальну природу, що і економічний об'єкт, що вивчається, тобто технологічні процеси повинн моделюватися технологічними процесами, а поведінка людей в економічному процесі, що вивчається - також діями людей. Для вивчення функціонування якого-небудь крупного підприємства можна було б використовувати невелике підприємство, проведення дослідження на якому обійшлося б дешевшим. Для аналізу діяльності великої групи підприємств можна було б узяти одне підприємство, а потім результати дослідження перенести на всю групу. Ця ідея виглядає дуже принадною. Спроби її реалізувати виявилися в наший країні в так званих "економічних експериментах", які почали проводитися з другої половини шістдесятих років. Метою цих досліджень був аналіз різних конкретних форм систем стимулювання виробництва, їх дії на підвищення ефективності діяльності підприємств. Найбільшу популярність здобули дослідження нових типів систем матеріального стимулювання (в Щекинськом об'єднанні " Азот" і в Главмосавтотрансе). Виника питання про те, чи можна подібні дослідження вважати експериментами на основ матеріальних моделей або вони є дослідженнями якого-небудь іншого типу. Для відповіді на це питання доцільно порівняти "економічні експерименти" з експериментами в природних науках. Проводячи дослідження моделі літака в аеродинамічній трубі, дослідник знає, які параметри літака і потоку набігаючого газу впливають на результати експерименту, яким чином відмінність цих параметрів в модельному експерименті від параметрів літака і атмосфери пов'язана з відмінністю в його силах, що цікавлять, і температурах і т.д. В "економічних експериментах" справа йде інакше. Звичайно, значна частина виробничий-технологічних чинників, що впливають на виробництво (кількість основних фондів, чисельність трудящих і їх кваліфікація, вартість продукції, що випускається, і її номенклатура в укрупнених показниках), ясні, і під час переходу підприємства до підприємства вплив зміни цих величин можна врахувати. Але окрім таких спостережуваних величин є та інші, приховані від зовнішнього спостерігача. По-перше, це виробничий-технологічні чинники типу неповного використання устаткування, втрат робочого часу, можливості зміни якост сировини і номенклатури вироблюваної продукції. Величини цих чинників можуть бути (з величезними витратами зусиль дослідників-економістів) встановлені для одного підприємства, але проводити такий аналіз для всіх підприємств, на як переноситимуться результати "економічного експерименту", просто неможливо. Але найголовніше навіть не в цьому, а в тому, що є ще і інші, так би мовити, людські чинники виробництва: відносини між людьми в колективі, відносини керівництва підприємства з суміжними підприємствами, місцевими властями і вищестоящою організацією. Ці чинники, дуже виробництва, що сильно впливають на ефективність, вивчаються "соціологією" проте поки успіхи в цій області науки ще не достатні для того, щоб на їх основі зміряти людськ чинники виробництва. Наявність соціально-економічних чинників, які не можуть бути зміряні і проконтрольовані в "економічному експерименті", не дозволяє рахувати таке дослідження модельним експериментом, його швидше можна зіставити з польовим випробуванням в техніці. Третій тип матеріального моделювання - аналогове моделювання - викликав великі над дослідників економічних систем в сорокових - п’ятдесятих роках. Ці над рунтувалися на кібернетичних принципах, головне місце в яких займає ідея про аналогію процесів управління в системах різної природи. Робилися спроби побудувати такі електричні схеми, динаміка фізичних величин в яких нагадувала б поведінку економічних величин. Аналізуючи ці схеми, дослідники сподівалися виявити закономірності економічних процесів. Незабаром, проте, стало ясно, що ці надії не виправдалися. Звичайно, економічні явища мають деякі риси, як можна інтерпретувати на основі тих, що набули широкого поширення кібернетичних понять (скажімо, таких як зворотний зв'язок і т.д.), проте аналогія між економічними системами і електричними схемами виявляється поверхневою даремною, оскільки в економічних процесах зворотні зв'язки реалізуються значно складнішими механізмами, ніж в електричних схемах. У зв'язку з цим аналогове моделювання в даний час в економіці практично не використовується, а кібернетичні ідеї реалізуються на основі математичних моделей Отже, матеріальне моделювання може застосовуватися для аналізу економічних явищ в украй обмеженому об'ємі. На відміну від матеріального, ідеальне моделювання економічних процесів використовується широко і постійно. Теоретичн дослідження, направлені на вивчення економічних явищ, протягом довгого часу рунтувалися на неформалізованому моделюванні, яке залишалося головним і єдиним засобом аналізу. Поява формалізованих образних моделей, а потім і математичних моделей створило передумови для точного опису економічних явищ і їх строгого аналізу за допомогою методів математики і логіки. Масове використання досягнень математики в гуманітарних науках, таких як економіка, соціологія, психологія, тільки починається. Лише у XX столітті з'явилися розділи математики, ведучі своє походження від проблем гуманітарних наук; найбільш відомий з них - теорія ігор. З кожним десятиліттям математика все глибше проникає в методи вивчення процесів, що відбуваються в людському суспільстві, , треба думати, використання математичних моделей в гуманітарних науках знаходитиме все більш широке застосування. Необхідно, проте, підкреслити, що на шляху проникнення математичних методів в гуманітарні науки, в економіку зокрема, зустрічаються об'єктивні труднощі, які і пояснюють той факт, що успіхи застосування математичного моделювання в економіці не так великі, як хотілося б, особливо але порівнянню з природними павуками. Дослідження математичної моделі дає змогу діставати характеристики реального економічного об’єкта чи системи. Тип математичної моделі залежить як від природи системи, так і від задач дослідження. У загальному випадку математична модель системи містить опис множини можливих станів останньої та закон переходу з одного стану до іншого (закон функціонування). Розглянемо основн типи економіко-математичних моделей, які класифікують за різними критеріями. За цільовим призначенням економіко-математичні моделі поділяються на теоретико-аналітичні, застосовувані для дослідження загальних властивостей і закономірностей економічних процесів (наприклад, модель Кейнса), та прикладні, призначені для розв’язування конкретних економічних задач (моделі економічного аналізу, прогнозування, управління тощо). Економіко-математичн моделі можуть бути призначені для дослідження як різних функціональних складових економіки (виробничо-технологічної, соціальної, територіально структури), так і його окремих частин. Розглядають моделі всієї економіки в цілому та її підсистем - секторів, галузей, регіонів, комплексів моделей виробництва, споживання, формування та розподілу прибутків, трудових ресурсів, ціноутворення, фінансових зв’язків тощо. Згідно із загальною класифікацією математичних моделей вони поділяються на функціональн та структурні, охоплюючи проміжні форми (структурно-функціональні). У дослідженнях на макрорівні найчастіше використовуються структурні моделі, оскільки для планування та управління велике значення мають взаємозв’язки підсистем. Типовими структурними моделями є моделі міжгалузевих зв’язків. Функціональн моделі широко застосовуються в економічному регулюванні, коли на поводження об’єкта ("вихід") впливають, змінюючи "вхід". Прикладом може бути модель поведінки споживачів за умов товарно-грошових відносин. Один той самий об’єкт може описуватися водночас як структурною, так і функціональною моделлю. За характером відображення причинно-наслідкових зв’язків розрізняють детерміновані моделі та моделі, що враховують випадковість і невизначеність - стохастичні. Залежно від урахування часового чинника економіко-математичні моделі поділяються на статичні та динамічні. У статичних моделях усі залежності стосуються одного моменту або періоду часу. Динамічні моделі характеризують зміни економічних процесів у часі. За тривалістю періоду часу, що розглядається, розрізняють моделі короткострокового (до року), середньострокового (до 5 років), довгострокового (10-15 і більше років) прогнозування та планування. Час в економіко-математичних моделях може змінюватися безперервно або дискретно. Тому розрізняють неперервні та дискретні моделі Моделі економічних процесів надзвичайно різноманітні за формою математичних залежностей. У загальному випадку виокремлюють лінійні та нелінійні моделі. Особливо важливим клас лінійних моделей, найзручніших для аналізу й розрахунків, завдяки чому вони набули великого поширення. Відмінності між лінійними та нелінійними моделями істотні не лише з математичного, а й з теоретико-економічного погляду. Адже численні залежності в економіці як на макро-, так і на мікро-рівні мають принципово нелінійний характер: вплив податкової та грошово-кредитної політики на економічних суб’єктів, ефективність використання ресурсів з розширенням виробництва, зміна обладнання, модел управління запасами тощо. Теорія "лінійної економіки" істотно відрізняється від теорії "нелінійної економіки". Від того, якими - опуклими чи не опуклими - вважаються множини виробничих можливостей підсистем (галузей, підприємств), істотно залежать висновки про можливості поєднання централізованого планування та господарської самостійності економічних підсистем. За співвідношенням екзогенних і ендогенних змінних, які включаються до моделей, останні поділяють на відкриті і замкнені. Повністю відкритих моделей не існує; модель повинна мати хоча б одну ендогенну змінну. Повністю замкненими (такими, що не містять жодної екзогенної змінної) економіко-математичні моделі бувають надзвичайно рідко. Загалом економіко-математичні моделі різняться за ступенем відкритості. Макроекономічн моделі поділяють на агреговані та деталізовані. Залежно від того, чи містять ц моделі просторові чинники та умови, чи ні, розрізняють моделі просторові та точкові. Отже, загальна класифікація економіко-математичних моделей охоплює понад десять основних ознак. З розвитком економіко-математичних досліджень проблема класифікац застосовуваних моделей дедалі ускладнюється. Поряд з появою нових типів моделей (особливо мішаних типів) і нових ознак їх класифікації відбувається інтеграція моделей різних типів у складніші модельні конструкції. Розглянемо основн етапи економіко-математичного моделювання. Процес моделювання передбача наявність трьох структурних елементів: об’єкта дослідження; суб’єкта (дослідник); модель, яка опосередковує відносини між суб’єктом і об’єктом. Побудова економіко-математичних моделей у загальному випадку складається з розглянутих далі етапів. 1.2 Етапи побудови економіко-математичних моделей1. Постановка економічної проблеми та її якісний аналіз. Головне - чітко сформулювати сутність проблеми (цілі дослідження), припущення, які приймаються, і т питання, на які необхідно одержати відповіді. Цей етап включає виокремлення найважливіших рис і властивостей об'єкта, що моделюється, і абстрагування від другорядних; вивчення структури об'єкта і головних залежностей, що поєднують його елементи; формулювання гіпотез, що пояснюють поведінку і розвиток об'єкта. 2. Побудова математичних моделей. Це - етап формалізації економічної проблеми, вираження у вигляді конкретних математичних залежностей і відношень (функцій, рівнянь, нерівностей тощо). Спочатку зазвичай визначається основна конструкція (тип) математично моделі, а потім уточнюються деталі цієї конструкції (конкретний перелік змінних параметрів, форма зв'язків). Однак надмірна складність і деталізованість моделі утруднює процес дослідження. Однією з важливих особливостей математичних моделей є потенційна можливість їх використання для вирішення різноманітних проблем. Тому, навіть зустрічаючись з новою економічною задачею спочатку необхідно спробувати застосувати для розв'язання цієї задачі вже відомі модел (адаптувати їх до задачі). У процесі побудови моделі здійснюється зіставлення двох систем наукових знань - економічних і математичних. Треба прагнути до того, щоб одержати модель, яка належить до добре вивченого класу математичних задач (напр. шляхом деякого спрощення вихідних положень моделі), Однак можлива й така ситуація, коли формалізація економічної проблеми приводить до невідомо раніше математичної структури. 3. Математичний аналіз моделі. Метою цього етапу є з'ясування загальних властивостей моделі. Найважливіший момент доведення існування рішень у сформованій моделі (теорема існування). Якщо математична задача не має рішення, то необхідність у наступній роботі відпадає; слід скоригувати чи постановку економічної задачі, чи модифікувати математичну формалізацію. Аналітичне дослідження моделі порівняно з емпіричним (числовим) має ту перевагу, що одержувані висновки зберігають свою силу за різноманітних конкретних значень зовнішніх і внутрішніх параметрів моделі. І все-таки моделі складних економічних об'єктів з великими труднощами піддаються аналітичному дослідженню. У тих випадках, коли аналітичними методами не вдається з'ясувати загальні властивості моделі, а спрощення модел спричиняється до недопустимих (неадекватних) результатів, переходять до числових методів дослідження. 4. Підготовка вихідної інформації. Моделювання висуває жорсткі вимоги до системи інформації. Водночас реальні можливості одержання інформації обмежують вибір моделей, як пропонуються до практичного використання. До уваги береться не лише можливість підготовки інформації, але й витрати на підготовку відповідних інформаційних масивів. Ці витрати не повинні перевищувати ефект від використання додатково нформації. до уваги У процесі підготовки інформації широко використовуються методи теорії ймовірностей, теоретичної і математичної статистики. 5. Числов розв'язки. Цей етап включає розробку алгоритмів для числового розв'язування задачі, складання програм на ЕОМ і безпосереднє проведення розрахунків. Труднощ цього етапу зумовлені передусім великою розмірністю економічних задач, необхідністю опрацювання значних масивів інформації. Звичайно розрахунки на підставі використання економіко-математичної моделі мають багатоваріантний характер. Дослідження, які проводяться за допомогою числових методів, можуть стати суттєвим доповненням до результатів аналітичного дослідження. 6. Аналіз числових результатів та їх використання. На цьому етапі виникає питання про правильність повноту результатів моделювання, про рівень практичного застосування останніх. Математичні методи перевірки можуть виявляти некоректність підходу до побудови моделі. Неформальний аналіз теоретичних висновків і числових результатів, як одержують за допомогою моделі, зіставлення їх із знаннями, якими володіємо, фактами дійсності також дозволять знаходити недоліки постановки економічно задачі, сконструйованої математичної моделі. Тому спершу перевіряють адекватність моделі за тими властиво-тями, що було взято за найістотніші. Тобто потрібно виконати верифікацію і валідацію моделі, оскільки головна мета моделювання полягає в розв’язуванні практичних задач (аналіз економічних об’єктів, економічне прогнозування, вироблення управлінських рішень т. ін). Верифікація модел - перевірка правильності структури (логіки) моделі. Валідація моделі - перевірка відповідності здобутих у результаті моделювання даних реальному процесу в економіці. Перелічені етапи економіко-математичного моделювання перебувають у тісному взаємозв’язку, зокрема можуть існувати зворотні зв’язки між етапами. Так, на етапі побудови моделі може з’ясуватися, що постановка задачі суперечлива чи призводить до занадто складної математичної моделі. Тоді вихідну постановку доводиться коригувати. [10] Найчастіше потреба повернутися до попереднього етапу постає на етапі підготовки вихідно нформації. Якщо необхідної інформації немає або її пошук тягне за собою велик витрати, доводиться повертатися до етапу формалізації і пристосовуватися до наявної інформації. Отже, моделювання являє собою циклічний процес. За останнім етапом необхідно переходити до першого й уточнювати постановку задачі згідно зі здобутими результатами, потім - до другого й уточнювати (коригувати) математичний модуль, далі - до третього т.д. 1.3 Особливост побудови математичної моделі економічного явища чи процесуМатематична модель економічного явища чи процесу - це його спрощений образ, поданий у вигляд сукупності математичних співвідношень (рівнянь, нерівностей, логічних співвідношень, графіків тощо). Модель ма адекватно описувати реальні технологічні та економічні процеси. У моделі потрібно враховувати все істотне, суттєве в досліджуваному явищі чи процесі, нехтуючи всім другорядним, неістотним у ньому. Математичне моделювання - це мистецтво, вузька стежка між переспрощенням та переускладненням. Справді, прості моделі не забезпечують відповідної точності, і "оптимальні" розв’язки за такими моделями, як правило, не відповідають реальним ситуаціям, дезорієнтують користувача, а переускладнені моделі важко реалізувати на ЕОМ як з огляду на неможливість їх інформаційного забезпечення, так і через відсутність відповідних методів оптимізації. Модель має бути зрозумілою для користувача, зручною для реалізації на ЕОМ. Необхідно, щоб множина змінних xj була не порожньою. З цією метою в економіко-математичних моделях за змоги слід уникати обмежень типу "=", а також суперечливих обмежень. Наприклад, ставиться обмеження щодо виконання контрактів, але ресурсів недостатньо, аби їх виконати 1.4 Методи економіко-математичного моделювання1.4.1 Множинна лінійна регресія. Множинна лінійна регресія в стандартизованому масштабіДля дослідження статистичної залежності лінійну регресію можна записати в стандартизованій формі. Розглянемо два методи оцінки параметрів множинної лінійної регресії в стандартизованому масштабі. Перший метод одержання оцінок параметрів лінійної регресії в стандартизованому масштабі Для цього величини показника і факторів приводяться до стандартизованого виду.
У стандартизованому масштабі спрощується лінійне стохастичне співвідношення між показником і факторами. Регресія не має вільного члена і в стандартизованому масштаб набуває вигляду.
Якщо для оцінки параметрів стандартизованої лінійної регресії використати МНК, то система нормальних рівнянь набуде вигляду.
……………………………………………………,
Якщо врахувати, що
……………………………….,
Якщо для
розв'язування системи нормальних рівнянь застосувати правило Крамера, то для
оцінки стандартизованого параметра
Аналогічно знаходиться оцінка для i-го стандартизованого коефіцієнта регресії.
Звідки легко
отримати зв'язок між стандартизованими оцінками параметрів і параметрів
регресії Якщо відома оцінка
параметра регресії Зміна фактора Другий метод одержання оцінок параметрів лінійної регресії в стандартизованому масштабі. Якщо розглядати множинну регресію в n-мірному просторі, то вона проходить через n-мірну точку з координатами середніх статистичних значень факторів і показника.
Розділимо рівняння
(1.5 7) на.
Враховуючи відношення між стандартизованими величинами і параметрами, запишемо в стандартизованому масштабі лінійну множинну регресію у вигляді. [18]
1.4.2 Множинна нелінійна регресіяНайбільш досконалою і вивченою серед усіх багатовимірних регресивних моделей є лінійна. Лише деякі природні та економічні процеси можна моделювати за допомогою лінійно моделі. її вибір залежить від процесу і тривалості спостереження за ним. Деяк процеси при нетривалому спостереженні за ними можна з певним наближенням моделювати за допомогою лінійної багатофакторної моделі. Для повного опису процесу, Як правило, необхідно використовувати нелінійні регресійні залежності. В економіці для деяких процесів такі залежності відомі. Як приклад можна назвати виробничу функцію Кобба-Дугласа. Використання ЕОМ дає змогу по-новому підійти до вивчення процесів, що залежать від багатьох факторів. Як і для парного регресійного аналізу, для багатофакторного регресійного аналізу можна розглядати два типи моделей: лінійні відносно оцінюваних параметрів та нелінійні відносно оцінюваних параметрів. [19] Багатофакторн регресійні моделі першого типу представлена у вигляді рівняння.
Де
Оцінки параметрів прогнозу і надійних інтервалів знаходять спочатку для лінійної моделі, а потім переходять до нелінійної моделі. Окрем багатофакторні, нелінійні відносно параметрів, моделі можна зводити до багатофакторних лінійних регресійних моделей. Прикладом таких багатофакторних моделей може бути модель
Регресіями такого виду можна описувати процеси, що залежать від досягнутого рівня прогресу без стотних обмежень на ці процеси. Логарифмуванням і наступною заміною змінних таку модель можна звести до лінійної. Для прикладу розглянемо регресію такого вигляду.
Для приведення регресії (1.5 13) до лінійної прологарифмуємо її:
Величини показника
Для загальност
запису системи нормальних рівнянь введемо позначення
Для оцінки параметрів регресії (1.5 15) система нормальних рівнянь має вигляд
……. ………………………………………………………………, (1.5 16)
Якщо det Запишемо систему нормальних рівнянь (1.5 16) у вигляді симплекс-таблиці в матричній формі
Якщо визначник det
1.4.3 Метод БрандонаПо цьому методу рівняння регресії записується у вигляді:
Де Порядок
розташування чинників |
|

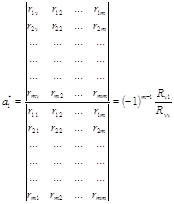 . (1.5 5)
. (1.5 5)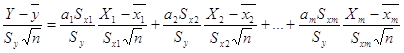 . (1.5 8)
. (1.5 8)