|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Курсовая работа: Економіко-математичне моделювання в управлінні підприємством аграрно-промислового комплексу
Обчислюємо середн квадратичне відхилення.
Далі ми обчислюємо коефіцієнт регресії
Тому: Обчислюємо параметри моделей:
Модель має вигляд:
Тепер вважаємо, що А3 обчислили неточно і обчислимо прогнозні значення. Зводимо розрахунок в таблицю.
Судячи з
розрахунків модель
Проводимо ти ж самі розрахунки що і раніше і отримуємо:
Вважаємо що А1 обчислений неточно і обчислимо прогнозні значення:
Обчисливши
значення
другий
Краще визначати другим методом (середньогеометричним) він простіший так як розрахунок проводиться через логарифм.
Тоді Після всіх розрахунків прогнозна модель буде мати вигляд.
Розрахунок прогнозу зручно привести у вигляді таблиці.
Тепер розраховуємо
залежність показника Для розрахунку
методом Брандона вибираємо таке значення Тоді:
де:
Знаходимо середн квадратичне відхилення.
Тепер обчислюємо коефіцієнт регресії:
Обчислення такі:
Наступна операція: Обчислення параметрів моделі:
За нашими розрахунками модель має вигляд:
Визначимо значення
А2 И
Припустимо, що А2 обчислили неточно, обчислюємо прогнозні значення. Запишемо їх у таблицю.
Наступним фактором
за ступенем зменшення коефіцієнта парної кореляції є Залишимо
позначення змінних U і Z такими ж, але значення цих змінних будуть іншими. Обчислимо
Розрахунок запишемо у таблицю:
Визначаємо середн значення:
Знаходимо середн квадратичне відхилення.
Обчислюємо
коефіцієнт регресії для
Обчислюємо параметри моделей:
Тоді модель ма вигляд:
Далі з U і Z
проробляємо ту ж операцію і обчислюваний А3 і.
Якщо з
обчислимо:
Або То
Тому:
Тепер вважаємо, що А3 обчислили неточно і обчислимо прогнозні значення: розрахунок зводимо у таблицю.
Третя зміна за ступенем зменшення коефіцієнта парної кореляції - х1. Залишимо позначення змінних U і Z такими ж, але значення цих змінних будуть іншими. Наші розрахунки запишемо у таблицю:
З наших попередніх
розрахунків видно що модель
Проводимо ти ж самі розрахунки що і раніше і отримуємо:
Вважаємо що А1 обчислений неточно і обчислимо прогнозні значення: Обчисливши
значення Його можна визначити двома способами. Перший спосіб: за допомогою формули
другий
Краще визначати другим методом (середньогеометричним) він простіший так як розрахунок проводиться через логарифм.
Тоді
Після всіх розрахунків прогнозна модель буде мати вигляд.
Розрахунок прогнозу зручно привести у вигляді таблиці.
3.2 Комп’ютерна реалізація методу БрандонаСистемні вимоги. Мінімальним системними вимогами є: Microsoft Excel 2000, що функціонує під керуванням операційних систем Windows 98/ME/NT/2000/XP. Опис програмних засобів Щоб провести сво розрахунки за методом Брандона я використовував комп'ютер, Microsoft Office Excel 2003 і VISUAL BASIC for Applications. Розрахунок методом Брандона складається з декількох операцій. При запуску файлу Brandon. xls на екрані з'явиться головне вікно (рисунок 3.1.1)
Рисунок 3.1.1 Головне вікно. На рисунку 3.1.1 вказан показники і фактори економіко-математичні моделі за допомогою яких буде відбуватися прогнозування. Кнопка "Початкові дані" дозволяє перейти у наступне вікно програми для введення вхідної статистики.
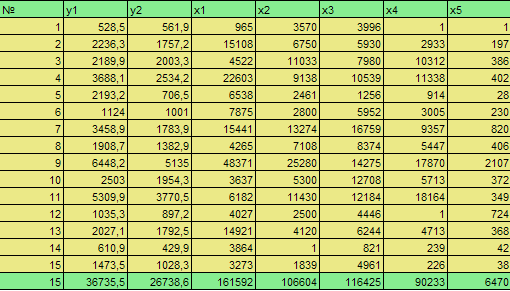
Рисунок 3.1.2 Вікно з початковими даними. На рисунку 3.1.2 зображена таблиця з початковими даними (рисунок 3.1 3).
Рисунка 3.1.3 Таблиця з початковими даними. При натисканні на кнопку "Прогноз для Y1" ми переходимо до вікна в якому відображень результат розрахунків для Y1 - валова продукція по собівартості за рік. (рисунок 3.1.4)
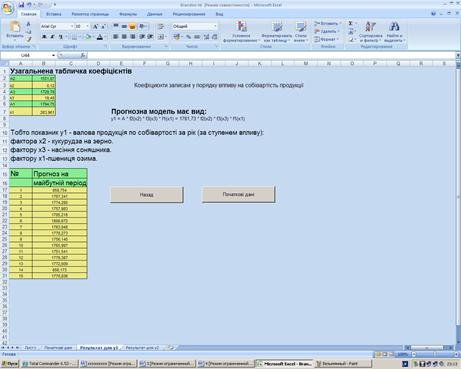
Рисунок 3.1.4 Вікно з результатами розрахунку для Y1. Аналогічно при натисканні на кнопку "Прогноз для Y2" ми переходимо до вікна в якому відображень результат розрахунків для Y2 - доход від реалізації. (рисунок 3.1.5)
Рисунок 3.1.5 Вікно з результатами розрахунку для Y2. Це дуже зручно для тих людей кому важливий тільки результат, і для тих яким не цікавий сам процес розрахунку. Розрахунки представлені у вигляді таблиці (рисунок 3.1 6)
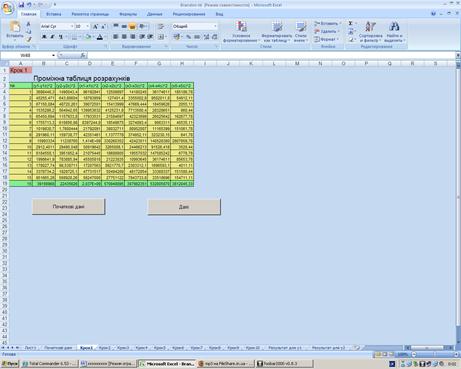
Рисунок 3.1.6 Таблиця з результатами розрахунків. На рисунках 3.1.4 3.1.5 знаходиться кнопка "ПОЧАТКОВІ ДАНІ". За допомогою якої ми можемо повернутися у вікно з початковими даними. Ввести нові дані і знову виконати розрахунок. На рисунку 3.1.2 знаходяться кнопки "РОЗРАХУНОК ДЛЯ Y1" і "РОЗРАХУНОК ДЛЯ Y2" за допомогою яких ми можемо проглянути покрокове виконання розрахунків даного методу для Y1 - валова продукція по собівартості за рік, і для Y2 - доход від реалізації. Всього у даному методі 17 кроків. При натисненні на кнопку "Розрахунок" на екрані відкривається вікно в якому відображено процес розрахунку представлений на рисунку 3.1.7
Рисунок 3.1 7 Друге вікно розрахунків. Також у цьому вікні знаходяться кнопки "Назад" і "Далі". За допомогою яких ми можемо повернутися у попереднє вікно, або перейти у наступне вікно розрахунків. Як мовилося раніше, таких вікон у розрахунках сімнадцять, і у кожному вікні є кнопки "НАЗАД" "ДАЛІ", за допомогою яких ми чи повертаємось у попереднє вікно, чи переходимо у наступне. 3.3 Функціональні можливості програми прогнозування урожайностіУ даній систем користувач сам здійснює введення інформації, а саме значення фінансових результатів за певний період, а також фактори. що мають вплив на цей показник. Програма знаходить оцінки параметрів побудованої регресійної моделі, а потім за бажанням користувача, визначає значення прогнозу будує графік, що дає можливість візуально побачити зміну показника за обраний період та зробити висновки своєї господарсько діяльності Введена інформація підлягає візуальному контролю, який полягає у перегляді на екрані набраної інформації і звірення її з первинними документами ВисновокСучасна економіка не буде працювати на потрібному рівні без ефективного керування. Успіх керування багато в чому визначається ефективністю прийняття рішень, що враховують самі різнобічні фактори і тенденції динаміки їхнього розвитку. Зрозуміло, для розкриття всіх потенційних можливостей, що несе в собі використання ресурсів, необхідно застосовувати економіко-математичне моделювання щоб знайти оптимальний варіант застосування можливостей підприємства. У випускній робот була проаналізована економічна діяльність підприємств, визначено значення економіко-математичного моделювання в управлінні підприємства, проаналізований ринок сільськогосподарської продукції і зроблений висновок про необхідність використання економіко-математичного моделювання в управлінні підприємства аграрно-промислового комплексу. Методом Брандона проведене прогнозування урожайності. Інформація, яку містять данні розрахунки можуть бути використана для прогнозування економічно діяльності через визначення впливу окремих видів продукції на загальну валову продукцію по собівартості, і на загальний дохід від реалізації. Перелік використаної літератури1. Бусленко Н.П. Моделирование сложных систем, - Главная редакция физико-математической литература изд-ва "Наука". - М., 1968, 356 с. 2. Девятков В. Построение моделей с помощью ПК. - "Компьютерра" №21 от 11 июля 2003 года. 3. Савицкая Г.В. Анализ хозяйственной деятельности предприятия: 4-е изд., перераб. и доп. - Минск: ООО "Новое знание", 1999. - 688 с. 4. Лотов А.В. Введение в экономико-математическое моделирование. - Главная редакция физико-математической литература изд-ва "Наука". - М., 1984, 392 с. 5. Томашевский В.Н., Жданова Е.Г., Жолдаков А.А. Решение практических задач методами компьютерного моделирования. - Киев: "Корнейчук", 2001. - 268 с. 6. Костенко Ї.Д., Підгора Є.О., Рижиков В.С., Панков В.А. Герасимов А.А., Ровенська В.В. Економічний аналіз і діагностика стану сучасного підприємства: Навчальний посібник. Київ, 2005. - 400 с. 7. Бочаров В.В. Финансовый анализ. Учебное пособие. Питер. 2004. - 240с. 8. Моделювання та методи системного аналізу в економіці. - К.:, 1999. - 120с. 9. Єріна Антоніна Михайлівна Статистичне моделювання та прогнозування. - К.: КНЕУ, 2001. - 170с. 10. Економіко-математичне моделювання соціально-економічних систем: Збірник наук. праць. Вип.3. - К., 2002. - 133с. - 6.80 11. Бахрушин, Володимир Євгенович Математичне моделювання: Навч. посіб. - Запоріжжя: ГУ "ЗІДМУ", 2004. - 140с. - 7.00 12. Потрашкова, Людмила Володимирівна. Моделювання управління розвитком підприємства: Спец.: 08.03.02; Автореф. дис. канд. екон. наук. - Харків, 2002. - 20с. 13. Управління підприємницькою діяльністю: оцінка, організація, прогнозування. - Суми: Університетська книга, 1999. - 333с. 14. Новаківський, Ігор Іванович Інформаційний потенціал системи управління підприємством: Спец.08.06.01. Автореф. Дис. на здоб. Наук. Ступ. Канд. Економ. Наук. - Львів, 2002. - 20с. 15. Касьяненко Володимир Олексійович, Старченко Людмила Володимирівна Моделювання та прогнозування економічних процесів. - Суми: Університетськя книга, 2006. - 356с 16. Глонь Ольга Віталіївна, Дубовий Володимир Михайлович Моделювання систем керування в умовах невизначеності. - Вінниця: Універсум, 2005. - 170с. 17. Кафаров В.В. Методы кибернетики в химии и химической технологии. - Москва издательство "Химия" 1976 462с. 18. Толбатов Ю.А. Економетрика. - Київ "Четверта хвиля", 1997. - 319с. 19. С.І. Наконечний, Т.О. Терещенко, Т.П. Романюк. Економетрія. Київ 1997. - 351с. 20. Наконечный C.И., Андрийчук В.Г. Математическое моделирование экономических процессов сельскохозяйственного производства. Учеб. Пособие. - Киев: КИНХ, 1982. - 106 с. 21. Голицина О.Л., Максимов Н.В., Попов И.И. Базы данных: Учебное пособие. - М.: ФОРУМ: ИНФРА-М, 2003. - 352 с. 22. Джексон Г. Проектирование реляционных баз данных для использования с микроЭВМ. - М.: Мир, 1991. - 252 с. 23. Карпова Т.С. Базы данных: модели, разработка, реализация. - СПб.: Питер, 2002. - 304 с. 24. Кириллов В.В. Структуризованный язык запросов (SQL). - СПб.: ИТМО, 1994. - 80 с. |

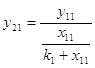 ;
; 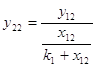 ;
;  и т.д.
и т.д. 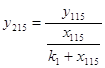 ;
;