|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Дипломная работа: Анализ режимов работы электрических сетей ОАО "ММК им. Ильича" и разработка адаптивной системы управления режимами электропотребленияДипломная работа: Анализ режимов работы электрических сетей ОАО "ММК им. Ильича" и разработка адаптивной системы управления режимами электропотребленияМинистерство образования и науки Украины Приазовский государственный технический университет Факультет информационных технологий Кафедра автоматизации энергетических систем и электропривода Специальность “Системы управления производством и распределением электроэнергии” МАГИСТЕРСКАЯ РАБОТА по специальности 8.090615 “Системы управления производством и распределением электроэнергии” на тему: Анализ режимов работы электрических сетей ОАО "ММК им. Ильича" и разработка адаптивной системы управления режимами электропотребления Студент Трубчанинова Анна Васильевна Руководитель Нормоконтроль Рецензент Проект рассмотрен на заседании кафедры и допущен к защите в ГЭК Зав. кафедрой АЭС и ЭП В.Н. Кравченко Мариуполь 2006 г "УТВЕРЖДАЮ" Зав. кафедрой АЭС и ЭП _____________ В.Н. Кравченко ЗАДАНИЕ на аттестационную работу магистра Трубчанинова Анна Васильевна 1. Тема работы Исследование режимов работы электрических сетей ОАО "ММК им. Ильича" и разработка адаптивной системы управления режимами электропотребления Тема утверждена приказом по ПГТУ №12-05 от 1 февраля 2006 г. 2. Цель исследования Определение оптимальных режимов работы электрических сетей. Разработка программного обеспечения для расчета оптимальных режимов работы электрических сетей. 3. Исходные данные (характеристика объекта, условий исследования и др.) Однолинейные схемы замещения электрических сетей. Графики нагрузок подстанций. 4. Основные задачи исследования: Определить диапазон изменения параметров электрических сетей и нагрузок в рабочих и типовых аварийных режимах. Исследовать и выбрать наиболее эффективные методы оптимизации режимов сетей. 5. Срок представления работы к защите - 1 июня 2006 г. 6. Дата выдачи задания - 1 сентября 2005 г. Научный руководитель _______________________ Задание принял к выполнению _________________ Календарный план
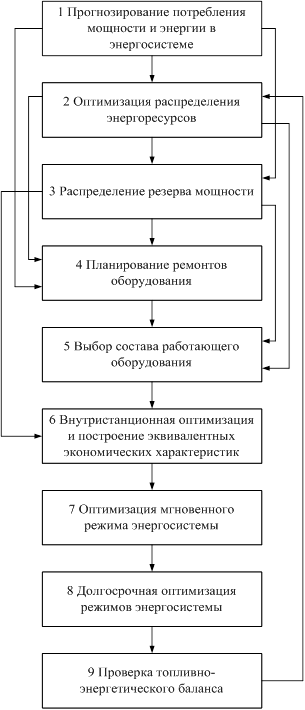
Студент _____________________________ Руководитель проекта _________________ Реферат Пояснительная записка: 96 страниц, 25 рисунков, 21 таблица, 3 приложения, 14 источников. Объект исследования: электрическая сеть ОАО ММК им. Ильича Рассмотрены вопросы оптимизации текущего режима электропотребления по реактивной мощности и разработки адаптивной системы управления режимами электропотребления. Разработано программное обеспечение по определению оптимальных режимов работы электрических сетей. Предложена система автоматизации процесса распределения реактивной мощности, реализованная на оборудовании фирмы Allen-Bradley. Разработанная система автоматизации производит сбор необходимых параметров, рассчитывает текущий режим, определяет оптимальные мощности компенсирующих устройств и передает управляющие воздействия на устройства, регулирующие мощности компенсирующих устройств. ОПТИМИЗАЦИЯ, ЭЛЕКТРОПОТРЕБЛЕНИЕ, РЕАКТИВНАЯ МОЩНОСТЬ, АКТИВНАЯ МОЩНОСТЬ, ПОТЕРИ МОЩНОСТИ, АВТОМАТИЗАЦИЯ Abstract Explanatory note: 96 page, 25 drawings, 21 tables, 3 exhibits, 14 sources. Object of research: electric network OAO MMK im. Iliicha Considereded questions of optimization current mode electroconsumptions on reactive power and development adaptive managerial system by modes of electroconsumption. Designeded software on determination of optimum states of working electric networks. Offereded system to automation of process of distribution reactive power marketed on equipping the company Allen-Bradley. Designeded system to automations produces the collection of necessary parameters, calculates the current mode, defines the optimum power compensating device and will send (pass) controlling influences on device, regulative power compensating device. OPTIMIZATION, ELECTROCONSUMPTION, REACTIVE POWER, ACTIVE POWER, LOSS a POWER, AUTOMATION Содержание Введение........................................................................................................... 9 1 Исследование методов оптимизации. 17 1.1 Основные понятия и определения оптимизации. 17 1.3 Методы решения оптимизационных задач. 19 1.3.1 Общая характеристика методов решения задач нелинейного программирования 19 1.4.1.3 Описание алгоритма метода. 24 1.4.3 Методы случайного поиска. 27 1.4.4 Метод покоординатного спуска. 29 1.5.1 Градиентный метод с постоянным шагом. 31 1.5.2 Метод скорейшего спуска. 32 1.5.3 Метод проектирования градиента. 35 1.6 Метод штрафных функций. 38 1.7 Методы полиномиальной аппроксимации. 39 1.7.1 Квадратичная аппроксимация. 40 1.7.2 Кубическая интерполяция. 43 1.7.3 Квадратичные функции. 46 1.9 Метод неопределенных множителей Лагранжа. 54 1.10 Выбор метода оптимизации. 56 2 Разработка метода оптимизации по реактивной мощности. 58 3 Разработка программного обеспечения метода оптимизации. 66 4. Разработка адаптивной системы управления режимами электропотребления 73 4.1 Функции автоматизированной системы.. 73 4.2 Описание работы системы.. 73 4.2.1 Ввод системы в работу. 73 4.2.2 Работа системы в нормальном режиме. 74 4.2.3 Работа системы в случае изменения конфигурации сети. 75 4.3 Требования к оборудованию и программному обеспечению.. 77 4.4 Выбор оборудование для адаптивной системы.. 78 4.4.1.1 Устройства мониторинга PowerMonitor 79 4.4.1.2 Программное обеспечение RSEnergy для контроля электропотребления 80 4.4.2 Процессор для диспетчерского пункта. 80 4.4.3.1 Основные преимущества. 83 4.4.3.2 Минимальные требования RSLinx: 84 4.4.3.3 Различия между разными версиями программного обеспечения RSLinx 84 4.4.3.4 Версия программного обеспечения RSLinx Lite. 84 4.4.3.5 Версия программного обеспечения RSLinx OEM.. 85 4.4.3.6 Версия программного обеспечения RSLinx Professional 86 4.4.3.7 Версия программного обеспечения RSLinx Gateway. 87 4.4.3.8 Версия программного обеспечения RSLinx SDK.. 88 4.4.3.9 Графические функции SuperWho и RSWho. 89 5 Исследование и получение оптимальных режимов для ОАО "ММК им. Ильича" 90 5.1 Расчет параметров схемы замещения. 90 5.1.1 Теоретические положения. 90 5.1.2 Расчет параметров схем замещения линий. 93 5.1.3 Расчет параметров схем замещения трансформаторов. 93 5.2 Расчет сети при различных нагрузках. 100 Выводы........................................................................................................ 103 Перечень ссылок.......................................................................................... 104 Приложение А............................................................................................. 106 Приложение Б.............................................................................................. 118 Введение При исследовании режимов электрических сетей необходимо обратить особое внимание на явления, связанные с передачей реактивной мощности по сети, а также на способы ее компенсации. В отличие от активной мощности реактивная мощность, потребляется элементами сети и электроприемниками в соизмеримых количествах. При этом она может генерироваться не только на электрических станциях, но и в сети. В частности, генерация реактивной мощности емкостью линий является вынужденной. Реактивная мощность является практически удачной формой учета условий протекания периодических процессов в цепи переменного тока. Поскольку для обеспечения условий их протекания при допустимых параметра режима приходится применять специальные компенсирующие устройства, то возникает задача их наивыгоднейшего использования в условиях эксплуатации сети. При решении этой задачи целесообразно прежде всего выяснить, с какими дополнительными явлениями связана передача реактивной мощности по элементам сети и какое влияние эти явления оказывают на технико-экономические показатели работы систем электроснабжения. Как известно, передача реактивной мощности приводит к увеличению потерь напряжения в сети. С передачей реактивной мощности непосредственно связано увеличение нагрузки в соответствующих элементах сети. Отсюда следует также и увеличение потерь активной мощности в элементах системы электроснабжения, которое должно учитываться в балансе по системе, т. е. компенсироваться соответствующей дополнительной установленной мощностью оборудования электрических станций. Одновременно увеличиваются потери энергии за любой промежуток времени. Дополнительный расход электроэнергии означает дополнительный расход энергоносителей, практически — топлива, что связано с дополнительными денежными и материальными расходами. Это означает, что для выполнения поставленной вначале задачи в действительности требуется генерация соответственно большей реактивной мощности, т. е. практически установка дополнительных компенсирующих устройств. Следует обратить внимание и на вторичное явление. Указанное выше увеличение потерь напряжения при неограниченной величине высшего допустимого напряжения приводит к снижению его низшего значения у приемного конца сети. А это приводит к увеличению значений токов при тех же значениях передаваемой мощности и к дополнительной потере активной и реактивной мощности, а также к дополнительной потере энергии. При наличии соответствующих компенсирующих устройств целесообразно компенсировать реактивную мощность на месте, по возможности устраняя передачу ее по элементам сети на большие расстояния. Однако надо иметь в виду, что включение в работу новых устройств или увеличение нагрузки уже работающих иногда приводит к увеличению потерь активной мощности в них. Наивыгоднейшее решение заранее может быть неизвестно и получается путем расчета. В распределительных сетях, особенно в промышленности, обычно имеет место потребление реактивной мощности в больших количествах. Основными потребителями реактивной мощности являются асинхронные двигатели, только намагничивающий ток которых составляет от 40 до 60% номинального. Компенсирующие устройства (батареи конденсаторов), устанавливаемые в распределительных сетях, могут быть использованы для регулирования напряжения. Это сокращает потребность в местных регулирующих устройствах. Поэтому экономичность работы компенсирующих устройств в распределительных сетях следует рассматривать с учетом воздействия на режим напряжений. При этом потери энергии в сети не обязательно получаются наименьшими, так же как и в случае распределения активной мощности между электрическими станциями в энергетической системе. Наибольшим должен быть результирующий экономический эффект. Другое положение получается при использовании реактивной мощности, генерируемой синхронными двигателями, которые могут быть установлены в промышленной распределительной сети. Генерация реактивной мощности синхронными двигателями приводит к аналогичном эффекту регулирования напряжения, но связана со значительными потерями активной мощности, а следовательно, и энергии в самих двигателях. Поэтому регулирование напряжения автоматическим изменением тока возбуждения синхронных двигателей не всегда экономически обосновано. Обычно использование для этого синхронных двигателей малой мощности экономически не оправдывается. В питающей сети, на всех приемных подстанциях которой имеются регулирующие устройства с достаточным регулировочным диапазоном, распределение реактивной мощности можно осуществлять по условиям экономичности работы самой питающей сети. Определяющими здесь являются условия минимума потерь активной мощности в сети при заданных ограничениях по наибольшему допустимому напряжению и рабочей реактивной мощности источников питания. В послеаварийных режимах перераспределением реактивной мощности в сети часто удается улучшить параметры режима. При этом экономичность режима приходится рассматривать как факт второстепенный. Комплексная проблема определения оптимальных условий эксплуатации энергосистем или энергообъединений должна решаться на основе использования экономического критерия минимизации приведенных народнохозяйственных затрат на производство и распределение электрической и тепловой энергии. Решение этой проблемы в настоящее время осуществляется на основе рассмотрения ряда взаимосвязанных задач, условно представленных на рисунке ниже. Каждая из перечисленных задач характеризуется своими частичным экономическим критерием и математической моделью поведения энергосистемы, которым отвечают определенные алгоритмы, наиболее полно учитывающие специфику задачи. В процессе решения используются различные исходные данные, в значительной мере вероятностные и неравноточные. Под задачей оптимизации текущего режима энергосистемы или энергообъединения понимают наивыгоднейшее распределение генерируемых активных и реактивных мощностей между электростанциями, а также другими регулируемыми источниками реактивной мощности — синхронными компенсаторами, управляемыми реакторами и батареями статических конденсаторов, которому отвечает минимум эксплуатационных издержек И на производство и распределение электрической и тепловой энергии в топливном или стоимостном выражениях: И(Z)=min. Целевая функция И зависит от вектора переменных Z, включающего в себя всю совокупность параметров режима. В зависимости от принятой математической модели
оптимизации, определяемой частичной задачей оптимизации и допущениями при
составлении модели, в состав Z могут входить активные и реактивные мощности
электростанций
Рис. Взаимосвязь различных задач оптимизации режимов Составляющие вектора Z связаны между собой рядом конкретных условий, накладываемых свойствами электрической сети, техническими характеристиками и условиями надежной работы оборудования. Сюда относятся обеспечение баланса мощностей, ограничение напряжений в узлах, ограничение тока и передаваемой мощности по линиям электропередачи, допустимость режимов по устойчивости параллельной работы электростанций, ограничение мощности электростанций по характеристикам оборудования и т. п. В такой общей постановке задача оптимизации текущего режима является многоэкстремальной задачей нелинейного математического программирования и для произвольного вида функции И(Z) строгие методы ее решения не разработаны. Из изложенного следует, что определения оптимального рабочего режима электрической сети в процессе ее текущей эксплуатации нужно значительное количество информации о параметрах режима и требуется выполнение достаточно сложных расчетов по ее обработке и получению ответа. В некоторых случаях задача должна решаться одновременно для всей энергетической системы. Для этого требуется достаточно сложное программное и аппаратное обеспечение, осуществляющее получение и обработку информации, а также управление всеми автоматизированными устройствами, имеющимися в системе. В своем дипломном проекте я оптимизирую текущий режим энергосистемы, а именно, минимизирую целевую функцию путем решения задачи нелинейного программирования на языке программирования С++. Задача безусловной минимизации (минимизации без ограничений) состоит в поиске минимума min f(х) , где функция f: R"®R - является по крайней мере непрерывной. Процедуры безусловной минимизации подразделяются на 3 категории: оперирующие функцией одной переменной; работающие с функцией нескольких переменных; использующие нелинейный метод наименьших квадратов. В случае функции одной переменной предполагается, что на исследуемом отрезке она имеет один экстремум. В противном случае осуществляется поиск локального минимума. Поиск минимума функции нескольких переменных можно выполнить квазиньютоновским методом, модифицированным алгоритмом Ньютона, методом сопряженных градиентов и методом деформируемого многогранника. Перечисленные процедуры обеспечивают поиск локального минимума. Если же функция имеет несколько локальных минимумов и необходимо найти наилучший, то следует испытать разные начальные точки и интервалы поиска. С процедурами, использующими только значения функции, следует употреблять двойную точность. Также полезно использовать процедуры контроля производной, обеспечивающие проверку работы пользовательских процедур, оценивающих производные. Как уже указывалось, в настоящее время не существует единообразного подхода к задаче оптимизации мгновенного режима энергосистемы. Все многообразие практических методов использования ЦВМ можно классифицировать по некоторым главным направлениям. Основными задачами расчетов могут являться: а) комплексная оптимизация распределения активных и реактивных генерируемых мощностей и коэффициентов трансформации по условию минимума суммарного расхода или стоимости топлива в системе; б) оптимальное распределение активных мощностей между электростанциями с приближенным учетом потерь в сети по условию минимума суммарного расхода или стоимости топлива; в) оптимальное распределение реактивных мощностей между электростанциями и синхронными компенсаторами и выбор оптимальных коэффициентов трансформации регулируемых трансформаторов по минимуму потерь в сети. В расчетах в качестве математической модели установившегося режима используются либо полные уравнения установившегося режима, обычно уравнения узловых напряжений в форме баланса мощностей в узлах, либо упрощенные уравнения баланса активной мощности в целом по системе
1. Исследование методов оптимизации 1.1 Основные понятия и определения оптимизации Показатель, по величине которого оценивают, является ли решение оптимальным, называется критерием оптимальности.[1] В качестве критерия оптимальности наиболее часто принимается экономический критерий, представляющий собой минимум затрат (финансовых, сырьевых, энергетических, трудовых) на реализацию поставленной задачи. При заданной или ограниченной величине указанных затрат экономический критерий выражается в получении максимальной прибыли. В электроэнергетике в зависимости от требований поставленной задачи могут применяться и другие критерии оптимальности, в частности: критерий надежности электроснабжения; критерий качества электроэнергии; критерий наименьшего отрицательного воздействия на окружающую среду (экологический критерий). Решение оптимизационной задачи включает в себя следующие этапы: сбор исходной информации (исходных данных); составление математической модели, под которой понимается формализованное математическое описание решаемой задачи; выбор метода решения, определяемого видом математической модели; выполнение математических вычислений, поручаемое, как правило, компьютеру; анализ решения задачи. Математическая модель Математическая модель – формализованное математическое описание оптимизационной задачи.[1,2] Математическая модель включает в себя: целевую функцию; ограничения; граничные условия. Целевая функция представляет собой математическую запись критерия оптимальности. При решении оптимизационной задачи ищется экстремум целевой функции, например минимальные затраты или максимальная прибыль. Обобщенная запись целевой функции имеет следующий вид:
где n - общее количество переменных. Зависимость между переменными в целевой функции (1.1) может быть линейной или нелинейной. Ограничения представляют собой различные технические,
экономические, экологические условия, учитываемые при решении задачи[1,2].
Ограничения представляют собой зависимости между переменными
Общее количество ограничений равно m. Граничные условия устанавливают диапазон изменения искомых переменных
где di и Di - соответственно нижняя и верхняя границы диапазона изменения переменной хi. Методы решения оптимизационных задач Для решения подавляющего большинства оптимизационных задач используются методы математического программирования, позволяющие найти экстремальное значение целевой функции (1.1) при соотношениях между переменными, устанавливаемых ограничениями (1.2), в диапазоне изменения переменных, определяемом граничными условиями (1.3). Математическое программирование представляет собой, как правило, многократно повторяющуюся вычислительную процедуру, приводящую к искомому оптимальному решению.[2,3] Выбор метода математического программирования для решения оптимизационной задачи определяется видом зависимостей в математической модели, характером искомых переменных, категорией исходных данных и количеством критериев оптимальности. Общая характеристика методов решения задач нелинейного программирования Когда целевая функция (1.1) и ограничения (1.2) нелинейны и для поиска точки экстремума нельзя или очень сложно использовать аналитические методы решения, тогда для решения задач оптимизации применяются методы нелинейного программирования. Как правило, при решении задач методами нелинейного программирования используются численные методы с применением ЭВМ[3,4,5,6]. В основном методы нелинейного программирования могут быть охарактеризованы как многошаговые методы или методы последующего улучшения исходного решения. В этих задачах обычно заранее нельзя сказать, какое число шагов гарантирует нахождение оптимального значения с заданной степенью точности. Кроме того, в задачах нелинейного программирования выбор величины шага представляет серьезную проблему, от успешного решения которой во многом зависит эффективность применения того или иного метода. Разнообразие методов решения задач нелинейного программирования как раз и объясняется стремлением найти оптимальное решение за наименьшее число шагов. Большинство методов нелинейного программирования используют идею движения в n-мерном пространстве в направлении оптимума. При этом из некоторого исходного или промежуточного состояния Uk осуществляется переход в следующее состояние Uk+1 изменением вектора Uk на величину DUk, называемую шагом , т.е.
В ряде методов шаг ,т.е. его величина и направление определяется как некоторая функция состояния Uk
Следовательно, согласно (1.4) новое состояние Uk, получаемое в результате выполнения шага (1.5) может рассматриваться как функция исходного состояния Uk
В некоторых методах DUk обусловлен не только состоянием Uk, но и рядом предшествующих состояний
Естественно, что алгоритмы поиска типа (1.8) являются более общими и принципиально могут обеспечить более высокую сходимость к оптимуму, т.к. используют больший объем информации о характере поведения оптимальной функции. В настоящее время для решения подобных задач разработано значительное число методов, однако нельзя отдать предпочтение какому- либо одному. Выбор метода определяется сложностью объекта и решаемой задачей оптимизации. Методы решения задач нелинейного программирования (условной многопараметрической оптимизации) подразделяют следующим образом: методы прямого поиска; градиентные методы; методы штрафных функций; методы полиномиальной аппроксимации. Методы прямого поиска Одними из методов нахождения минимума функции n-переменных являются методы прямого поиска. Методы прямого поиска являются методами, в которых используются только значения функции[1,7]. В методах прямого поиска ограничения учитываются в явном виде. Необходимость разработки этих методов связана с тем, что в инженерных приложениях часто приходится сталкиваться с случаями, когда целевые функции не заданы в явном виде. Эти методы строятся на интуитивных соображениях, не подкреплены строгой теорией и, следовательно, не гарантируется их сходимость. Несмотря на это, в силу своей логической простоты эти методы легко реализуются. Перед непосредственным применением методов прямого поиска необходимо провести ряд мероприятий по подготовке задачи к решению, а именно исключить ограничения в виде равенств; определить начальную допустимую точку. Простейший способ исключения ограничений в виде равенств заключается в решении его относительно одной из переменных с последующим исключением этой переменной путем подстановки полученного выражения в соотношения, описывающие задачу. При этом следует учитывать, что границы значений исключаемых переменных сохраняются в задаче в виде ограничений - неравенств. Несмотря на то, что подстановка является самым простым способом исключения ограничений - равенств, не всегда оказывается возможным ее осуществить. В этом случае проблема решается путем численного решения уравнения относительно зависимых переменных при заданных значениях независимых оптимизирующих переменных. Для определения начальной допустимой точки целесообразно использовать процедуру случайного поиска, основная идея которого будет рассмотрена ниже. После проведения процедуры подготовки задачи к решению следует приметить один из методов условной оптимизации[5,6]. Рассмотрим методы прямого поиска: модифицированный метод Хука-Дживса; метод комплексов; метод случайного поиска; метод покоординатного спуска. 1.4.1 Метод Хука-Дживса Одним из методов прямого поиска есть метод Хука-Дживса[5,7], который был разработан в 1961г, но до сих пор является весьма эффективным и оригинальным. Метод Хука-Дживса характеризуется несложной стратегией поиска, относительной простотой вычислений и невысоким уровнем требований к памяти ЭВМ. Это один из первых алгоритмов, в котором при определении нового направления поиска учитывается информация, полученная на предыдущих итерациях. Процедура Хука-Дживса представляет собой комбинацию исследующего поиска с циклическим изменением переменных и ускоряющего поиска по образцу. 1.4.1.1 Исследующий поиск Для проведения исследующего поиска необходимо знать величину шага, которая может быть различной для разных координатных направлений и изменяться в процессе поиска. Исследующий поиск начинается в некоторой исходной точке. Если значение целевой функции в пробной точке не превышает значение в исходной точке, то шаг поиска рассматривается как успешный. В противном случае надо вернуться в предыдущую точку и сделать шаг в противоположном направлении с последующей проверкой значения целевой функции. После перебора всех n- координат исследующий поиск завершается. Полученную в результате точку называют базовой точкой. 1.4.1.2 Поиск по образцу Поиск по образцу [5,6] заключается в реализации единственного шага из полученной базовой точки вдоль прямой, соединяющей эту точку с предыдущей базовой точкой. Новая точка образца определяется в соответствии с формулой Xp(k+1)=X(k)+(X(k)-X(k-1)). (1.9) Как только движение по образцу не приводит к уменьшению целевой функции, точка Xp(k+1)фиксируется в качестве временной базовой точки и вновь проводится исследующий поиск. Если в результате получается точка с меньшим значением целевой функции, чем в точке X(k), то она рассматривается как новая базовая точка X(k+1). С другой стороны, если исследующий поиск неудачен, необходимо вернуться в точку X(k) и провести исследующий поиск с целью выявления нового направления минимизации. В конечном счете возникает ситуация, когда такой поиск не приводит к успеху. В этом случае требуется уменьшить величину шага путем введения некоторого множителя и возобновить исследующий поиск. Поиск завершается, когда величина шага становится достаточно малой. Последовательность точек, получаемую в процессе реализации метода, можно записать в следующем виде: X(k) - текущая базовая точка, X(k-1)- предыдущая базовая точка, Xp(k+1)- точка, построенная при движении по образцу, X(k+1)- следующая (новая) базовая точка. Приведенная последовательность характеризует логическую структуру поиска по методу Хука-Дживса. 1.4.1.3Описание алгоритма метода Шаг 1. Выбрать начальную базисную точку b1 и шаг длиной hj для каждой переменной xj, j=1,2,...,n. Шаг 2. Вычислить f(x) в базисной точке b1 с целью получения сведений о локальном поведении функции f(x). Функция f(x) в базисной точке b1 находится следующим образом: Вычисляется значение функции f(b) в базисной точке b1. Каждая переменная по очереди изменяется прибавлением длины шага. Таким образом, мы вычисляем значение функции f(b1+h1*e1), где e1-единичный вектор в направлении оси х1. Если это приводит к уменьшению значения функции, то d1 заменяется на b1+h1*e1. В противном случае вычисляется значение функции f(b1-h1*e1), и если ее значение уменьшилось, то b1 заменяем на b1-h1*e1. Если ни один из проделанных шагов не приводит к уменьшению значения функции, то точка b1 остается неизменной и рассматриваются изменения в направлении оси х2, т.е. находится значение функции f(b1+ h2*e2) и т.д. Когда будут рассмотрены все n-переменныx, мы будем иметь новую базисную точку b2. Если b2=b1, т.е. уменьшение функции не было достигнуто, то исследование повторяется вокруг той же базисной точки b1, но с уменьшенной длиной шага. Если b2 Шаг 3. При поиске по образцу используется информация, полученная в процессе исследования, и минимизация функции завершается поиском в направлении, заданном образцом. Эта процедура производится следующим образом: Разумно двигаться из базисной точки b2 в направлении b2-b1, поскольку поиск в этом направлении уже привел к уменьшению значения функции. Поэтому вычислим функцию в точке образца P1=b1+2*(b2-b1). (1.10) В общем случае Pi=bi+2*(b(i+1)-bi). (1.11) Затем исследование следует продолжать вокруг точки P1(Pi). Если наименьшее значение на шаге B,2 меньше значения в базисной точке b2(в общем случае b(i+1)), то получают новую базисную точку b3 (b(i+2)), после чего следует повторить шаг B,1 . В противном случае не производить поиск по образцу из точки b2(b(i+1)), а продолжить исследования в точке b2(b(i+1)). |
|

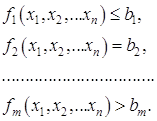 (1.2)
(1.2)