|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Дипломная работа: Анализ режимов работы электрических сетей ОАО "ММК им. Ильича" и разработка адаптивной системы управления режимами электропотреблениягарантирует вашим приложениям высокую эффективность и надежную передачу данных; позволяет вашим приложениям совместно использовать коммуникационные драйверы со средствами программирования фирмы Rockwell Software и HMI. 4.4.3.9 Графические функции SuperWho и RSWho Пункт меню Communications/Super Who выводит на экран все доступные/активные станции коммуникационной сети в окне SuperWho. Основное назначение SuperWho – это показать вам вашу сеть. В режиме Normal (нормальный) или Fast (быстрый) SuperWho представляется в текстовом виде. В графическом (Graphical) режиме SuperWho представляется как графический взгляд на вашу сеть. Вы можете видеть станции в сети, их номера и имена проектов. Поддерживаются следующие сети: Data Highway Plus, Data Highway 485 и Ethernet. SuperWho действует как инструмент диагностики, когда есть проблемы со связью с определенной станцией. Используя окно SuperWho, можно вывести на экран счетчики диагностики для любой станции, можно открыть окна счетчиков диагностики для нескольких станций в одной коммуникационной сети. RSWho - это новый интерфейс просмотра RSIinx, заменивший более ранний интерфейс SuperWho. Он позволяет вам просматривать все активные связи на одном экране (см. рис. 4.3). 5. Исследование и получение оптимальных режимов для ОАО "ММК им. Ильича" 5.1 Расчет параметров схемы замещения 5.1.1 Теоретические положения
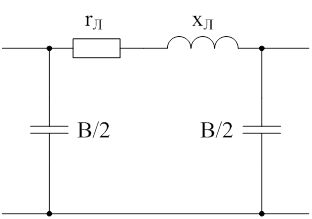
Рисунок 5.1 – Схема замещения линии 110-220 кВ Активное, реактивное сопротивления линии и емкостная проводимость соответственно рассчитываются по формулам[9,13]:
где
Рисунок 5.2 – Схема замещения двухобмоточного трансформатора
Рисунок 5.3 – Схема замещения трехобмоточного трансформатора Расчет активных сопротивлений:
Отсюда
Расчет реактивных сопротивлений:
Опыт холостого хода проводится аналогично опыту для двухобмоточного трансформатора, поэтому активные и реактивные проводимости в трехобмоточном трансформаторе рассчитываются по тем же формулам (5.7) и (5.8). 5.1.2 Расчет параметров схем замещения линий Кабель АСБГ 4(3*240) длина 540 м: r=70.2 Ом. АС-240 длина 604 м: r=78,52 Ом, x=241.6 Ом; В=1721,4*10-6 См. АС-400 длина 634 м: r =50,72 Ом, x=240,9 Ом; В=1902*10-6 См. АС-240 длина 686 м: r =89,18 Ом, x=274,4 Ом; В=1955*10-6 См. 5.1.3 Расчет параметров схем замещения трансформаторов Таблица 5.1 – Номинальные параметры трехобмоточного трансформатора п/ст Ильич
Согласно формулам (5.9), (5.11) имеем: rT=1,5 Ом, х1=56,9 Ом, х2=0, х3=35,7 Ом. Согласно (5.6)-(5.7): GT=0.0023, BT=0.013. Таблица 5.2 – Номинальные параметры двухобмоточного трансформатора п/ст Ильич
Согласно формулам (5.4) - (5.7) имеем: rT=1,42 Ом, хТ=34,7 Ом, GT=0.0027, BT=0.02. Таблица 5.3 – Номинальные параметры двухобмоточного трансформатора Т1 п/ст 28, Т2 п/ст 37
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=0.92 Ом, хТ=23 Ом, GT=0.0038, BT=0.0272. Таблица 5.4 - Номинальные параметры двухобмоточного трансформатора Т2 п/ст 28, Т1 и Т2 п/ст 20.
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=0.87 Ом, хТ=22 Ом, GT=0.0045, BT=0.0286. Таблица 5.5 - Номинальные параметры двухобмоточного трансформатора п/ст 32
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=1,42 Ом, хТ=34,7 Ом, GT=0.0027, BT=0.0197. Таблица 5.6 - Номинальные параметры двухобмоточного трансформатора Т1 п/ст 33
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=1,42 Ом, хТ=34,7 Ом, GT=0.0027, BT=0.0197. Таблица 5.7 - Номинальные параметры двухобмоточного трансформатора Т2 п/ст 33
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=1,9 Ом, хТ=44 Ом, GT=0.0045, BT=0.0167. Таблица 5.8 - Номинальные параметры трехобмоточного трансформатора п/ст 6, п/ст 42, Т1 - Т2 п/ст 41
Согласно формулам (5.9), (5.11) имеем: rT=0,8 Ом, х1=35,5 Ом, х2=0, х3=22,3 Ом. Согласно (5.6)-(5.7): GT=0.0033, BT=0.0181. Таблица 5.9 - Номинальные параметры двухобмоточного трансформатора Т1 п/ст 44
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=1,42 Ом, хТ=34,7 Ом, GT=0.0027, BT=0.0197. Таблица 5.10 - Номинальные параметры двухобмоточного трансформатора Т2 п/ст 44, п/ст 43
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=1,9 Ом, хТ=44 Ом, GT=0.0045,BT=0.0167. Таблица 5.11 - Номинальные параметры двухобмоточного трансформатора Т1 п/ст 34, п/ст 46
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=4,38 Ом, хТ=86,7 Ом, GT=0.0014, BT=0.0085. Таблица 5.12 - Номинальные параметры двухобмоточного трансформатора Т2 п/ст 34, п/ст 2
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=1,9 Ом, хТ=44 Ом, GT=0.0045, BT=0.0167. Таблица 5.13 - Номинальные параметры двухобмоточного трансформатора п/ст 38
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=1,42 Ом, хТ=34,7 Ом, GT=0.0027, BT=0.0197. Таблица 5.14 - Номинальные параметры двухобмоточного трансформатора Т1 п/ст 37
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=1,42 Ом, хТ=34,7 Ом, GT=0.0027, BT=0.0197. Таблица 5.15 - Номинальные параметры двухобмоточного трансформатора п/ст 40
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=1,9 Ом, хТ=44 Ом, GT=0.0045, BT=0.0167. Таблица 5.16 - Номинальные параметры двухобмоточного трансформатора п/ст 31: ТДНГ-40500/110/10
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=1,42 Ом, хТ=34,7 Ом, GT=0.0027, BT=0.0197. Таблица 5.17 - Номинальные параметры двухобмоточного трансформатора Т3, Т4 п/ст 41
Подставив номинальные параметры в (5.4) - (5.7) получим: rT=0,87 Ом, хТ=22 Ом, GT=0.0045, BT=0.0286. 5.2 Расчет сети при различных нагрузках На первом этапе (см. рис. 3.1) с помощью разработанного
программного обеспечения были рассчитаны неоптимальные режимы работы сети ОАО
"ММК им. Ильича" с компенсацией реактивной мощности при коэффициенте
реактивной мощности Таблица 5.18 - Оптимальный режим сети при номинальных нагрузках
Проведя расчет оптимального режима сети ОАО "ММК им.
Ильича" при номинальных нагрузках, было получено минимальное значение потерь
активной мощности в сети ΔРопт=84500 кВт. Эффект разработанного
программного обеспечения оценивается по снижению потерь активной мощности на
величину Таблица 5.19 – Оптимальный режим сети при максимальных нагрузках
Проведя расчет оптимального режима сети ОАО "ММК им.
Ильича" при максимальных нагрузках, было получено минимальное значение
потерь активной мощности в сети ΔРопт=89320 кВт. Эффект разработанного
программного обеспечения оценивается по снижению потерь активной мощности на
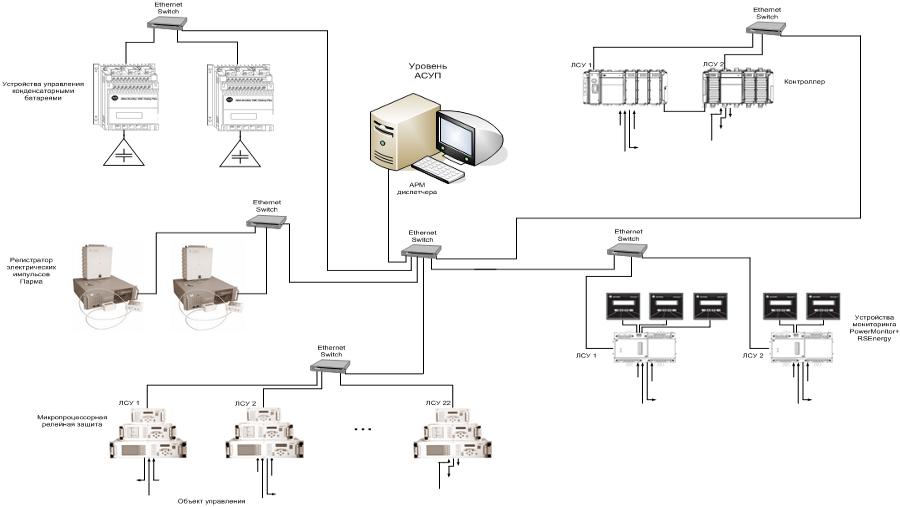
величину Выводы Разработанное программное обеспечение позволяет решить комплекс проблем, связанных с оптимальным распределением реактивной мощности по сети. Разработанная адаптивная система управления позволяет осуществлять постоянный контроль над нагрузками подстанций и конфигурацией сети, оперативно реагировать на какие-либо изменения и производить точный расчет для нового режима. Внедрение представленного комплекса, состоящего из программного обеспечения и адаптивной системы управления, на любое предприятие с любой сложно замкнутой сетью, в данном случае, на ОАО "ММК им. Ильича" позволяют: значительно уменьшить потери энергии; поддерживать постоянный уровень напряжения у приемного конца сети; значительно уменьшить денежные затраты на потребление и генерацию реактивной мощности. Минимум аппаратного обеспечения, необходимого для информационного режима работы адаптивной системы управления, и совместимость системы с любым оборудованием, уже установленного на подстанциях, позволяет сделать вывод о целесообразности применения разработанного программного обеспечения на ОАО "ММК им. Ильича" и других крупных промышленных предприятий. Перечень ссылок 1. В.Н. Костин.: Оптимизационные задачи электроэнергетики: Учеб. пособие. – СПб.: СЗТУ, 2003 – 120с. 2. В.Г. Карманов. Математическое программирование. – М.: Наука, 1980 – 256с. 3. Дж. Деннис, Р. Шнабель. Численные методы безусловной оптимизации и решения нелинейных уравнений. – М.: Мир, 1988 – 440с. 4. З.Н. Бененсон, М.Р. Елистратов, Л.К. Ильин и др. Моделирование и оптимизация на ЭВМ радиоэлектронных устройств. – М.: Радиосвязь, 1981 – 272с. 5. С. Гилл, У. Мюррей. Численные методы условной оптимизации. – М.: Мир, 1977 – 339с. 6. Васильев С.П. Численные методы решения экстремальных задач. – М.: Наука, 1980 – 518с. 7. И.Т. Черноруцкий. Методы оптимизации в теории управления, С.-П.: Питер, 2004 – 226с. 8. В.Е. Болконин, П.И. Чинаев. Анализ и синтез систем автоматического управления на ЭВМ. Алгоритмы и программы. – М.: Радио и связь, 1986 – 248с. 9. В.Н. Костин, Е.В. Распопов, Е.А. Родченко. Передача и распределение электроэнергии: Учеб. пособие. – СПб.: СЗТУ, 2003 – 147с. 10. Барзам А.Б. Системная автоматика. – М.: Энергоатомиздат, 1989. – 446с. 11. Баркан Я.Д., Орехов Л.А. Автоматизация энергосистем: учебное пособие для студентов вузов. – М.: Высш. школа, 1981. – 271с. 12. А. А. Черносвитов. Курс MCSD Visual C++ 6.0 и MFC, С.-П.: Питер, 2000 – 554с. 13. Веников В.А. Управление переходными режимами в электрических системах. – М.: Высшая школа, - 1972. – 352с. Приложение А Программа расчета оптимальных режимов #include <stdio.h> #include <complex.h> #include <iostream.h> #include <conio.h> #include <math.h> int luc ( int, complex [][31], int [], double ); void rluc ( int, complex [][31], int [], complex [] ); void gauss ( int n, complex [][31], complex [], complex * ); void rasis ( int, int, complex [], complex [], complex [], int [], int [] ); void start ( int, int, int, complex [][31], complex [], complex [], int [], int [], int [], int ); void vard ( int, int, int, complex [][31], complex [], complex [], int [], int [], int [] ); void varm ( int, int, int, complex [][31], complex [], complex [], int [], int [], int [] ); void prejc ( int, int, int, complex [], complex [] ); void rasis ( int, int, complex [], complex [], complex [], int [], int [] ); void pryzc ( int, complex [], int [], int [], int ); void foryzc ( int, int, complex [][31], complex [], int [], int [] ); double w; void main ( void ) { complex a[30][31], b[30], yz[90], tok[90], s; int imax[90], imin[90], irow[30]; int n, nyz, nej, istop, i, j; double f; do { clrscr ( ); scanf ( "%i4 %i4 %i4 %i4", &f, &n, &nyz, &nej, &istop ); w = 2 * M_PI * f; start ( n, nyz, nej, a, b, yz, imax, imin, irow, 0 ); for ( i = 0; i < nyz; i++ ) { yz[i] = 1.0 / yz[i]; cout << yz[i]; if ( ! ( i % 4 ) ) cout << '\n'; } for ( i = 0; i < nyz; i++ ) cin >> imax[i] >> imin[i]; cin >> n; vard ( n, nyz, nej, a, b, yz, imax, imin, irow ); rasis ( n, nyz, b, yz, tok, imax, imin ); } while ( istop ); //for ( i = 0; i < n; i++ ) //for ( j = 0; j <= n; j++ ) //cin >> a[i][j]; //for ( i = 0; i < n; i++ ) //b[i] = a[i][n]; //for ( i = 0; i < n; i++ ) //{ //for ( j = 0; j <= n; j++ ) //cout << a[i][j]; //cout << '\n'; //} //for ( i = 0; i < n; i++ ) //cout << b[i]; //luc ( n, a, irow, 0.00001 ); //rluc ( n, a, irow, b ); //cout << '\n'; //gauss ( n, a, b, &s ); //for ( i = 0; i < n; i++ ) //cout << b[i]; } int luc ( int n, complex a[][31], int irow[], double eps ) { int i, i1, j, k, l, n1; complex prom; for ( i = 0; i < n; i++ ) irow[i] = i; n1 = n - 1; for ( i = 0; i < n1; i++ ) { i1 = i + 1; l = i; for ( k = i1; k < n; k++ ) if ( abs ( a[k][i] ) > abs ( a[l][i] ) ) l = k; if ( abs ( a[l][i] ) < eps ) return 0; if ( l > i ) { for ( j = 0; j < n; j++ ) { prom = a[i][j]; a[i][j] = a[l][j]; a[l][j] = prom; } irow[i] = l; } for ( j = i1; j < n; j++ ) a[i][j] = a[i][j] / a[i][i]; for ( k = i1; k < n; k++ ) for ( j = i1; j < n; j++ ) a[k][j] -= a[k][i] * a[i][j]; } return 1; } void rluc ( int n, complex a[][31], int irow[], complex b[] ) { int i, j; complex sum; for ( i = 0; i < n; i++ ) if ( i != irow[i] ) { sum = b[i]; b[i] = b[irow[i]]; b[irow[i]] = sum; } for ( i = 0; i < n; i++ ) { sum = b[i]; for ( j = 0; j < i; j++ ) sum -= a[i][j] * b[j]; b[i] = sum / a[i][i]; } for ( i = n - 2; i >= 0; i-- ) { sum = b[i]; for ( j = i+1; j < n; j++ ) sum -= a[i][j] * b[j]; b[i] = sum; } } void gauss ( int n, complex a[][31], complex x[], complex *s ) { int i, j, k, l, k1, n1; complex r; n1 = n + 1; for ( k = 0; k < n; k++ ) { k1 = k + 1; *s = a[k][k]; j = k; for ( i = k1; i < n; i++ ) { r = a[i][k]; if ( abs ( r ) > abs ( *s ) ) { *s = r; j = i; } } if ( *s == complex ( 0.0, 0.0 ) ) break; if ( j != k ) for ( i = k; i < n1; i++ ) { r = a[k][i]; a[k][i] = a[j][i]; a[j][i] = r; } for ( j = k1; j < n1; j++ ) a[k][j] /= *s; for ( i = k1; i < n; i++ ) { r = a[i][k]; for ( j = k1; j < n1; j++ ) a[i][j] -= a[k][j] * r; } } if ( *s != complex ( 0.0, 0.0 ) ) for ( i = n - 1; i >= 0; i-- ) { *s = a[i][n]; for ( j = i + 1; j < n; j++ ) *s -= a[i][j] * x[j]; x[i] = *s; } return; } void start ( int n, int nyz, int nej, complex a[][31], complex b[], complex yz[], int imax[], int imin[], int irow[], int iy ) { int i; pryzc ( nyz, yz, imax, imin, iy ); for ( i = 0; i < nyz; i++ ) { cout << yz[i]; if ( ! ( i % 4 ) ) cout << '\n'; } vard ( n, nyz, nej, a, b, yz, imax, imin, irow ); } void vard ( int n, int nyz, int nej, complex a[][31], complex b[], complex yz[], int imax[], int imin[], int irow[] ) { int i, j; foryzc ( n, nyz, a, yz, imax, imin ); //for ( i = 0; i < n; i++ ) //{ //for ( j = 0; j < n; j++ ) //cout << a[i][j]; //cout << '\n'; //} if ( luc ( n, a, irow, 1.0e-5 ) ) varm ( n, nyz, nej, a, b, yz, imax, imin, irow ); else printf ( "\nв®з®Ґ аҐиҐЁҐ Ґ ў®§¬®¦®" ); return; } void varm ( int n, int nyz, int nej, complex a[][31], complex b[], complex yz[], int imax[], int imin[], int irow[] ) { int i; prejc ( n, nej, nyz, b, yz ); for ( i = 0; i < n; i++ ) { cout << b[i]; if ( ! ( i % 4 ) ) cout << '\n'; } rluc ( n, a, irow, b ); for ( i = 0; i < n; i++ ) { cout << b[i]; if ( ! ( i % 4 ) ) cout << '\n'; } return; } void pryzc ( int nyz, complex yz[], int imax[], int imin[], int iy ) { int i, indrlc; complex rlc; for ( i = 0; i < nyz; i++ ) { cin >> rlc >> indrlc >> imax[i] >> imin[i]; yz[i] = rlc; if ( indrlc == 2 ) yz[i] = complex ( 0.0, -1000000 / ( w * imag ( rlc ) ) ); if ( indrlc == 1 ) yz[i] = complex ( 0.0, w * imag ( rlc ) * 0.001 ); if ( indrlc == 3 ) yz[i] = polar ( real ( rlc ), imag ( rlc ) ); cout << "YZ[" << i+1 << "]= " << yz[i]; } } void foryzc ( int n, int nyz, complex a[][31], complex yz[], int imax[], int imin[] ) { int i, j, k, kolstr; for ( i = 0; i < n; i++ ) { for ( j = 0; j < n; j++ ) a[i][j] = complex ( 0.0, 0.0 ); //cout << '\n'; } for ( k = 0; k < nyz; k++ ) { i = imax[k]; j = imin[k]; a[i-1][i-1] += yz[k]; if ( j ) { a[j-1][j-1] += yz[k]; a[i-1][j-1] -= yz[k]; a[j-1][i-1] = a[i-1][j-1]; } } clrscr(); cout << "YZ[i][j]="; kolstr = 0; for ( i = 0; i < n; i++ ) { for ( j = 0; j < n; j++ ) { cout << "\nYZ[" << i+1 << "][" << j+1 << "]= " << a[i][j]; kolstr++; if ( kolstr == 22 ) { kolstr = 0; getchar ( ); clrscr(); cout << "YZ[i][j]="; } } } return; } void prejc ( int n, int nej, int nyz, complex b[], complex yz[] ) { int i, ind1, ind2, imin, imax, iyz; complex ej; for ( i = 0; i < n; i++ ) b[i] = complex ( 0.0, 0.0 ); for ( i = 0; i < nej; i++ ) { cin >> ej >> iyz >> imax >> imin >> ind1 >> ind2; if ( ind1 ) ej = polar ( real ( ej ), imag ( ej ) ); if ( ind2 ) ej *= yz[iyz-1]; cout << "ei= " << ej; b[imax-1] += ej; if ( imin ) b[imin-1] -= ej; } return; } void rasis ( int n, int nyz, complex b[], complex yz[], complex tok[], int imax[], int imin[] ) { int i, j, k; for ( k = 0; k < nyz; k++ ) { i = imax[k]; j = imin[k]; if ( j ) tok[k] = ( b[i-1] - b[j-1] ) * yz[k]; else tok[k] = b[i-1] * yz[k]; } for ( k = 0; k < nyz; k++ ) cout << "I["<< k+1 << "]=" << tok[k]; return; } Приложение Б Структурная схема системы управления
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 , (5.4)
, (5.4) (5.5)
(5.5)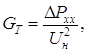 (5.6)
(5.6)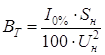 . (5.7)
. (5.7)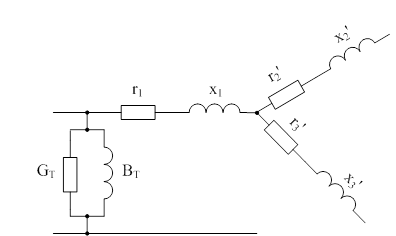
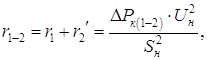
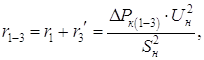
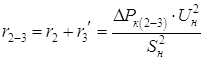 . (5.8)
. (5.8)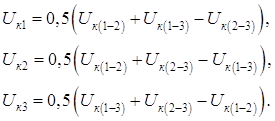 (5.10)
(5.10)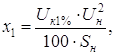
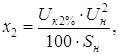
 (5.11)
(5.11)