|
Рефератыполиграфия и этнографии москвоведению и спорту языку |
Дипломная работа: Анализ режимов работы электрических сетей ОАО "ММК им. Ильича" и разработка адаптивной системы управления режимами электропотребленияШаг 4. Завершить этот процесс, когда длина шага (длины шагов) будет уменьшена до заданного малого значения. 1.4.2 Метод комплексов Алгоритм [7]: Заданы границы значений всех переменных xiL, xiU, i=1,2,..., N (размерность задачи), допустимая точка xo, параметр отображения a (рекомендуется a =1,3) и параметры окончания вычислений и d . Шаг 1. Построение начального комплекса, состоящего из P допустимых точек (рекомендуется P=2N). Для каждой точки p = 1, 2,...,P-1 случайным образом определить координаты xp; если xp - недопустимая точка, то найти центр тяжести xцт уже найденных точек и положить xp = xp + (xцт - xp); повторять процедуру до тех пор, пока xp не станет допустимой; если xp - допустимая точка, повторять до тех пор, пока p=P; вычислить W(xp) для p=0,1,...,P-1. Шаг 2. Отражение комплекса: выбрать точку xR, для которой W(xR) = max W(xp) = Wmax (решается задача минимизации); найти центр тяжести xцт и новую точку xm = xцт + a (xцт - xR); если xm - допустимая точка и W(xm)< Wmax, уменьшить в два раза расстояние между xm и центром тяжести xцт, продолжать поиск, пока W(xm)<Wmax; если xm - допустимая точка и W(xm)<Wmax, то перейти к шагу 4; если xm - недопустимая точка, то перейти к шагу 3. Шаг 3. Корректировка для обеспечения допустимости: если xim<xiL(нижняя граница допускаемой области), то положить xim = xiL; если xim>xiU(верхняя граница допускаемой области), то положить xim = xiU; если xm - недопустимая точка, то уменьшить в два раза расстояние до центра тяжести; продолжать до тех пор, пока xm не станет допустимой точкой. Шаг 4. Проверка условий окончания вычислений: положить
и
если
и
то вычисления прекратить; в противном случае перейти к шагу 2a. 1.4.3 Методы случайного поиска Наиболее простой процедурой случайного поиска [3,5] является прямая выборочная процедура, заключающаяся в разыгрывании на ЭВМ последовательности точек с координатами xi = xiL +ri (xiU - xiL), i=1,2,...,N, (1.12) где ri - случайная величина, равномерно распределенная на интервале [0,1]. После проверки каждой точки на допустимость вычисляются
значения целевой функции, которые сравниваются с наилучшим значением,
полученным к данному моменту. Если текущая точка дает лучшее значение, то она
запоминается, в противном - отбрасывается. Процесс прекращается после заданного
числа итераций N или по исчерпанию заданного машинного времени. Для получения
90% доверительного интервала величиной i (xiU - xiL), где 0<
<1, для переменной xi совместный случайный поиск требует Значительного увеличения эффективности процедуры случайного поиска можно достигнуть путем группировки выборок в серии. При этом наилучшая точка в каждой серии используется как начальная точка следующей серии, точки которой уже выбираются из интервала меньшей величины. Данная процедура получила название выборки со сжатием пространства поиска. Рассмотрим более подробно ее алгоритм. Заданы границы значений всех переменных xiL, xiU, i=1,2,..., N (размерность задачи), начальные допустимая точка xo и интервал поиска D xo = xiU - xiL, количество серий Q, количество точек в серии P и параметр окончания вычислений . Для каждой из серий, начиная с q = 1, необходимо выполнить следующие действия. Шаг 1. Для i = 1,2,...,N вычислить xip = xiq-1 +ri D xq-1, (1.13) где ri - случайная величина, равномерно распределенная на интервале [-0,5;0,5]. Шаг 2. если xp - недопустимая точка и p < P, то повторить шаг 1; если xp - допустимая точка, то запомнить xp и W(xp) и если p < P, то повторить шаг 1; если p = P, то найти среди всех допустимых точек xp точку с наименьшим значением W(xp) и положить ее равной xq. Шаг 3. Уменьшить интервал поиска, полагая D∙xiq = i∙D∙xiq-1. Шаг 4. Если q > Q, то закончить вычисления. В противном случае увеличить q=q+1 и продолжить вычисления, начиная с шага 1. 1.4.4 Метод покоординатного спуска
Рисунок 1.1 - Метод покоординатного спуска Рассмотрим функцию двух переменных. Ее линии уровня представлены на рис. 1.1, а минимум лежит в точке (x1*,x2*). Простейшим методом поиска является метод покоординатного спуска[3,4]. Из точки А произведем поиск минимума вдоль направления оси х1 и, таким образом, находим точку В, в которой касательная к линии постоянного уровня параллельна оси х1. Затем, производя поиск из точки В в направлении оси х2, получаем точку С, производя поиск параллельно оси х2, получаем точку D, и т.д. Таким образом, мы приходим к оптимальной точке. Очевидным образом эту идею можно применить для функции n переменных. Теоретически данный метод эффективен в случае единственного минимума функции. Но на практике он оказывается слишком медленным. Поэтому были разработаны более сложные методы, использующие больше информации на основании уже полученных значений функции. 1.5 Градиентные методы Как следует из названия, эти методы решения нелинейных
оптимизационных задач используют понятие градиента функции[3,5,7]. Градиентом
функции
где Величина этого вектора определяется по выражению
Из (1.14) и (1.15) видно, что функция, градиент которой определяется, должна быть дифференцируемой по всем n переменным. Физический смысл градиента функции в том, что он
показывает направление (1.14) и скорость (1.15) наибольшего изменения функции в
рассматриваемой точке. Если в некоторой точке 1.5.1 Градиентный метод с постоянным шагом Сущность градиентных методов решения нелинейных
оптимизационных задач [1,5,7] поясним для случая отыскания абсолютного минимума
функции двух переменных
Рисунок 1.2 – Иллюстрация градиентного метода с
постоянным шагом В соответствии с граничными условиями (1.3), в
большинстве практических оптимизационных задач они принимают только
положительные или нулевые значения, областью Выполним шаг единичной длины ( Далее вычислительная процедура повторяется: последовательно получаем 2-е, 3-е и 4-е приближения – точки с координатами х12, х22; х13, х23 и х14, х24. Значения целевой функции в этих точках соответственно составляют Z2, Z3 и Z4. Из рис. 1.2 видно, что в результате вычиcлительного
процесса последовательно осуществляется "спуск" к минимуму функции Z.
Вычислительная процедура заканчивается, когда относительное изменение целевой
функции на предыдущем i-м и последующем (i+1)-м шагах оказывается меньше
заданной точности вычислений
Рассмотренная вычислительная процедура носит название
градиентного метода с постоянным шагом. В этом методе все шаги выполнялись
одинаковой длины Для получения более точного результата необходимо выбрать шаг меньшей длины. При этом объем вычислений (количество шагов) увеличится. Таким образом, точность и объем вычислений в градиентном методе с постоянным шагом определяются величиной этого шага. 1.5.2 Метод скорейшего спуска Как было отмечено выше, при увеличении длины шага объем вычислений (количество шагов) уменьшается, однако уменьшается и точность определения минимума целевой функции. При уменьшении длины шага точность увеличивается, однако объем вычислений (количество шагов) возрастает. Поэтому вопрос о выборе рациональной длины шага в градиентных
методах является своего рода оптимизационной задачей. Один из способов
определения оптимальной длины шага
Рисунок 1.3 – Иллюстрация метода скорейшего спуска (а) и параболическая аппроксимация целевой функции для выбора оптимального шага (б) В методе наискорейшего спуска желательно использовать
рассмотренное свойство направления градиента. Поэтому, если мы находимся в
точке хi на некотором шаге процесса оптимизации, то поиск минимума функции
осуществляется вдоль направления -
где λi - значение λ, минимизирующее функцию.
Значение λi может быть найдено с помощью одного из методов одномерного поиска (например, методом квадратичной интерполяции). В приложении приведена программа, позволяющая реализовать метод наискорейшего спуска. В ней множитель Лагранжа обозначен через h. Вектор di является единичным. Для поиска минимума функции
в направлении di из точки xi используется метод квадратичной интерполяции. В точке
Данный оператор for(i=0;i<n;i++) g2+=g[i]*d[i]; - вычисляет выражение
Оператор if (ff[2]>=ff[0] || g2>=0) проверяет условие "перекрытия" минимума, которое выполняется при выполнении либо одного, либо другого условия. Если минимум не попал в отрезок (0,λ), то λ удваивается, и это повторяется столько раз, сколько необходимо для выполнения условия "перекрытия". Удостоверившись, что отрезок (0,λ) содержит минимум, в качестве третьей точки возьмем точку λ/ 2. Минимальную точку сглаживающего квадратичного полинома находим в соответствии с соотношением
что отражено следующими операторами l[3]=h*(ff[1]-.75*ff[0]-.25*ff[2]); l[3]/=2*ff[1]-ff[0]-ff[2]; Оператор for(i=0;i<n;i++) { x[i]=y[i]+l[0]*d[i]; y[i]=x[i]; } производит присваивание xi+1=xi, и если |g(xi+1)| достаточно мало, то процесс заканчивается. В процессе поиска предполагается сходимость к экстремуму, поэтому для эффективности процедуры разумно уменьшить длину шага. При этом деление шага пополам выбрано произвольно. В методе скорейшего спуска, по сравнению с градиентным методом с постоянным шагом, количество шагов меньше, точность получаемого результата выше, отсутствует зацикливание вычислительного процесса, однако объем вычислений на одном шаге больше. 1.5.3 Метод проектирования градиента Рассмотренные выше градиентные методы предполагали отыскание абсолютного минимума целевой функции Z. При наличии в математической модели нелинейных ограничений ищется уже не абсолютный, а относительный минимум целевой функции Z [1]. Рассмотрим один из методов отыскания относительного минимума целевой функции, получивший название метода проектирования градиента. Для упрощения алгоритма допустим, что имеется одно ограничение в виде линейного неравенства
При наличии указанного ограничения минимум целевой
функции следует искать в области Начало вычислительной процедуры такое же, как и в предыдущих методах: в области вычисляется значение целевой функции в этой точке Z0; в соответствии с выражением (1.15) в этой точке вычисляется градиент целевой функции grad Z; из исходной точки в направлении убывания целевой функции выполняется шаг.
Рисунок 1.4 – Иллюстрация метода проектирования градиента Выбор величины шага может осуществляться различным образом. Выберем шаг в соответствии с алгоритмом метода скорейшего спуска и получим первое приближение – точку с координатами х11, х21. Вычисляется значение целевой функции в этой точке Z1. Необходимо проверить, принадлежит ли точка с координатами
х11, х21 области
Если это неравенство выполняется, вычислительный процесс продолжается. Из точки с координатами х11, х21 выполняется следующий шаг. В результате этого шага имеем второе приближение – точку с координатами х12, х22. значение целевой функции в этой точке Z2. Пусть для этой точки неравенство Возврат в область Дальнейший спуск к относительному минимуму целевой
функции продолжается из точки х13, х23. на каждом шаге вычисляется значение
целевой функции и проверяется принадлежность нового приближения к области 1.6 Метод штрафных функций Рассмотрим задачу поиска локального минимума критерия оптимальности W в области, ограниченной системой неравенств (3.16)-(3.17). Введение обобщенного критерия оптимальности по методу штрафных функций [3,5] производится с помощью непрерывной функции
Обобщенным критерием оптимальности согласно методу штрафных функций является выражение T=W+RQ(x), где R - некоторое положительное число, называемое коэффициентом штрафа. Рассматривается некоторая неограниченная, монотонно возрастающая последовательность {Rk}, k=1,2,... положительных чисел. Для первого элемента этой последовательности с помощью метода покоординатного спуска отыскивается локальный минимум функции T. Пусть этот минимум достигается при значениях (b*,R1). Вектор (b*,R1) используется как начальное приближение для решения задачи поиска минимума функции T где R2>R1 и т.д. Таким образом, решается последовательность задач минимизации функций T(b*,Rk), k=1,2 ..., причем результат предыдущей оптимизации используется в качестве начального приближения для поиска последующей.
Рисунок 1.5 – Блок-схема метода штрафных функций 1.7 Методы полиномиальной аппроксимации Согласно теореме Вейерштрасса об аппроксимации, непрерывную функцию в некотором интервале можно аппроксимировать полиномом достаточно высокого порядка [6]. Следовательно, если функция унимодальна и найден полином, который достаточно точно ее аппроксимирует, то координаты точки оптимума функции можно оценить путем вычисления координаты точки оптимума полинома. Рассмотрим следующие вопросы: квадратичная аппроксимация; кубическая интерполяция; квадратичные функции. 1.7.1 Квадратичная аппроксимация Используется несколько значений функции в определенных точках для аппроксимации функции обычным полиномом по крайней мере в небольшой области значений. Затем положение минимума функции аппроксимируется положением минимума полинома, поскольку последний вычислитель проще. Простейший случай основан на том факте, что функция, принимающая минимальное значение во внутренней точке интервала, должна быть по крайней мере квадратичной. Если целевая функция W(x) в точках x1, x2, x3 принимает соответствующие значения W1, W2, W3, то можно определить коэффициенты aо, a1, a2 таким образом, что значения квадратичной функции q(x) = ao + a1(x - x1) + a2(x - x1)(x - x2) (1.25) совпадут со значением W(x) в трех указанных точках. Вычислим q(x) в трех указанных точках (см. табл.1.1). Таблица 1.1 - Вычисление значений
1.7.1.1Метод Пауэлла Если известны значения функции f(x) в трех разных точках α, β, γ равные соответственно fα, fβ, fγ, то функция f(x) может быть аппроксимирована квадратичной функцией ö(x)=Ax2+Bx+C, (1.26) где А, В и С определяются из уравнений Aá2+Bá+C=fá, Aâ2+Bâ+C=fâ, Aã2+Bã+C=fã. (1.27) После преобразований этих уравнений получаем A=[(ã-â)fá+(á-ã)fâ+(â-á)fã] / D, B=[(â2-ã2)fá+(ã2-á2)fâ+(á2-â2)fã] / D, C=[âã(ã-â)fá+ãá(á-ã)fâ+áâ(â-ã)fã] / D, (1.28) где D=(á-â)(â-ã)(ã-á) Ясно, что φ(x) будет иметь минимум в точке x=-B/2A, если А>0. Следовательно, можно аппроксимировать точку минимума функции f(x) значением
Этот метод может непосредственно применяться к функциям одной переменной. Он может быть очень полезен для выполнения линейного поиска в процедурах, описанных в теме №3. В этих процедурах требуется найти минимум функции f(x) в точках прямой x0+λd, где x0- заданная точка, а d определяет заданное направление. Значение функции f(x0+λd) на этой прямой является значениями функции одной переменной λ: φλ = f(x0+λd). (1.30) Идеи и результаты, изложенные выше, преобразуются в вычислительные процедуры, описанные далее. Предположим, что заданы унимодальная функция одной переменной f(x), начальная аппроксимация положения минимума и длинна шага D, является величиной того же порядка, что и расстояние от точки А до точки истинного минимума x*(условие, которое не всегда просто удовлетворить). Вычислительная процедура имеет следующие шаги: Шаг 1. x2 = x1 + D x. Шаг 2. Вычислить W(x1) и W(x2). Шаг 3. если W(x1) > W(x2), то x3 = x1 + 2 D x; если W(x1)< W(x2), то x3 = x1 - D x; W(x1) > W(x2), Шаг 4. Вычислить W(x3) и найти Wmin = min{ W(x1),W(x2), W(x3)}, Xmin = xi, соответствующая Wmin. Шаг 5. По x1, x2, x3 вычислить x*, используя формулу для оценивания с помощью квадратической аппроксимации. Шаг 6. Проверка окончания если | Wmin - W(x*)| < W, то закончить поиск. В противном случае к шагу 7; если | Xmin - x*| < x, то закончить поиск. В противном случае к шагу 7. Шаг 7. Выбрать Xmin или x* и две точки по обе стороны от нее. Обозначить в естественном порядке и перейти к шагу 4. Заметим, что если точка Е задана слишком малой, то á, â, ã, а также fá, fâ, fã будут очень близко друг к другу и значение d (1.29) может стать вообще недостижимыми. Чтобы преодолеть эту трудность, перепишем (1.29) для второй и последней интерполяции:
1.7.2 Кубическая интерполяция Квадратичная интерполяция, которая рассматривалась в предыдущем разделе, называется методом Пауэлла и аппроксимирует функцию квадратным трехчленом. В этом разделе рассматривается метод Давидона [6,7], который гарантирует большую точность и аппроксимирует функцию кубическим полиномом. Для кубической интерполяции в этом методе используются значения функции и ее производной, вычисленных в двух точках. Рассмотрим задачу минимизации функции f(x) на прямой x0 + hd , то есть минимизацию функции
Предположим, что известные следующие значения:
Эту информацию можно использовать для построения кубического полинома a+bh+ch2+dh3, который будет аппроксимировать функцию φ(h) Если p=0 , то уравнения, которые определяют a, b, c, d имеют вид :
Следовательно, если r является точкой минимума кубического полинома,
где
Одно из значений этого выражения является минимумом. Друга производная равна 2c +6dh. Если мы выберем положительный знак, то при
другая производная будет
Выбор точки q зависит от нас. Если Gp >0 , то надо выбрать значение q положительным, то есть сделать шаг в направлении уменьшения функции φ(h) , в другом случае значения q надо выбирать отрицательным. Значение должно быть таким, чтобы интервал (0, ) включал в себя минимум. Это будет верным, если φq > φ p или Gp >0. Если ни одно из этих условий не исполняется, то мы удваиваем значения q , повторяя это в случае необходимости, пока указанный интервал не будет содержать в себе минимум. Давидон, Флетчер и Пауэлл предложили выбирать q следующим путем:
где φm - оценка самого малого значения истинного минимума φ(h), h- константа, значение которой обычно берут 2 или 1. 1.7.3 Квадратичные функции Квадратичная функция [7,8]
где a - константа; b - постоянный вектор; G - положительно определенная симметричная матрица - имеет минимум в точке x* , где x* определяется следующим путем:
откуда
Любую функцию можно аппроксимировать в окрестности точки x0 функцией
где G(x0) - матрица Гессе, вычисленная в точке x0. Аппроксимацией минимума функции f(x) может быть минимум функции φ(x). Если последний находится в точке xm, то
откуда
или
Таким образом точкой xи следующей аппроксимации минимума будет:
или
где λи - длина шага, определяется одномерным поиском в направлении G-1(xи)g(xи). 1.8 Метод Нелдера-Мида Метод Нелдера-Мида (поиск по деформируемому многограннику) является развитием симплексного метода Спендли, Хекста и Химсворта [7,8]. Множество (n+1)-й равноудаленной точки в n-мерном пространстве называется регулярным симплексом. Эта конфигурация рассматривается в методе Спендли, Хекста и Химсворта. Следовательно, в двумерном пространстве симплексом является равносторонний треугольник, а в трехмерном пространстве правильный тетраэдр. Идея метода состоит в сравнении значений функции в (n+1) вершинах симплекса и перемещении в направлении оптимальной точки с помощью итерационной процедуры. В симплексном методе, предложенном первоначально, регулярный симплекс использовался на каждом этапе. Нелдер и Мид предложили несколько модификаций этого метода, допускающих, чтобы симплексы были неправильными. В результате получился очень надежный метод прямого поиска, являющийся одним из самых эффективных, если n<=6. В методе Спендли, Хекста и Химсворта симплекс перемещается с помощью трех основных операций: отражения, растяжения и сжатия. Смысл этих операций станет понятным при рассмотрении шагов процедуры. Шаг 1. Найдем значения функции в вершинах симплекса: f1=f( x1), f2=f(x2) ... fn+1=f(xn+1) (1.46) Шаг 2. Найдем наибольшее значение функции fh, следующее за наибольшим значением функции fg , наименьшее значение функции fl и соответствующие им точки xh, xg и xl. Шаг 3. Найдем центр тяжести всех точек, за исключением точки xh. Пусть центром тяжести будет
и вычислим f(x0)=f0. Шаг 4. Удобнее всего начать перемещение от точки xh. Отразив точку xh относительно точки x0, получим точку xr и найдем f(xr) = fr. Операция отражения иллюстрируется рис. 1.6.
Рисунок 1.6 – Операция отражения Если α>0 - коэффициент отражения, то положение точки xr определяется следующим образом: xr-x0=α (x0-xh), т.е. xr=(1+α)x0 -αxh. (1.48) Замечание. α= |xr-x0| / |x0 –xh|. Шаг 5. Сравним значения функций fr и fl. Если fr<fl, то мы получили наименьшее значение функции. Направление из точки x0 в точку xr наиболее удобно для перемещения. Таким образом, мы производим растяжение в этом направлении и находим точку xe и значение функции fe=f(xe). Рисунок 1.7. иллюстрирует операцию растяжения симплекса. Коэффициент растяжения γ1 можно найти из следующих соотношений: xe-x0=γ (xr-x0), т.е. xe=γxr+ (1-γ)x0. (1.49)
Рисунок 1.7 – Операция растяжения Замечание γ=|xe-x0| / |xr-x0| Если fe<fl, то заменяем точку xh на точку xe и проверяем (n+1)-ую точку симплекса на сходимость к минимуму (см. шаг 8). Если сходимость достигнута, то процесс останавливается; в противном случае возвращаемся на шаг 2. Если fe=fl , то отбрасываем точку xe. Очевидно, мы переместились слишком далеко от точки x0 к точке xr. Поэтому следует заменить точку xh на точку xr, в которой было получено улучшение (шаг 5, 1) проверить сходимость и, если она достигнута, вернуться на шаг 2. Если fr>fl, но fr <=fgто xr является лучшей точкой по сравнению с другими двумя точками симплекса и мы заменяем точку xh на точку xr и, если сходимость не достигнута, возвращаемся на шаг 2, т.е. выполняем пункт 1,б, описанный выше. Если fr>fl и fr>fgто перейдем на шаг 6. Шаг 6. Сравним значения функций fr и fh. Если fr>f h, то переходим непосредственно к шагу сжатия 6,2. Если fr<fh, то заменяем точку xh на точку xr и значение функции fh на значение функции fr. Запоминаем значение fr>f g из шага 5,2, приведенного выше. Затем переходим на шаг 6,2. В этом случае fr>f h, поэтому ясно, что мы переместились слишком далеко от точки xh к точке x0. Пытаемся исправить это, найдя точку xc (а затем fс) с помощью шага сжатия, показанного на рис. 1.8. Если fr>f h, то сразу переходим к шагу сжатия и находим точку xc из соотношения xc-x0=β(xh-x0), (1.50) где β(0<b<1)- коэффициент сжатия. Тогда xc=βxh+(1-β)x0. (1.51) Если fr<f h, то сначала заменим точку xh на точку xr, а затем произведем сжатие. Тогда точку xc найдем из соотношения xc-x0=β(xr-x0), т.е. xc=βxr+(1-β)x0. (1.52) Шаг 7. Сравниваем значения функций fc и fh. Если fc<f h, то заменяем точку xh на точку xc, и если сходимость не достигнута ,то возвращаемся на шаг 2. Если fc>f h, то очевидно, что все наши попытки найти значение меньшее fh закончились неудачей, поэтому мы переходим на шаг 8. На этом шаге мы уменьшаем размерность симплекса делением пополам расстояния от каждой точки симплекса до xl-точки, определяющей наименьшее значение функции.
Рисунок 1.8 - Шаг сжатия для fr>fh
Рисунок 1.9 - Шаг сжатия для fr<fh Таким образом, точка xi заменяется на точку
т.е. заменяем точку xi точкой Затем вычисляем fi для i=1,2,...,(n+1), проверяем сходимость и, если она достигнута, возвращаемся на шаг 2. Шаг 9. Проверка сходимости основана на том, чтобы стандартное отклонение (n+1) -го значения функции было меньше некоторого заданного малого значения. В этом случае вычисляется
где Если σ<ε, то все значения функции очень близки друг к другу, и поэтому они, возможно, лежат вблизи точки минимума функции xl. Исходя из этого, такой критерий сходимости является разумным, хотя Бокс, Дэвис и Свенн предлагают то, что они считают более "безопасной" проверкой. Коэффициенты αβγ в вышеприведенной процедуре являются соответственно коэффициентами отражения, сжатия и растяжения. Нелдер и Мид рекомендуют брать α=1, β=0.5 и γ=2. Рекомендация основана на результатах экспериментов с различными комбинациями значений. Эти значения параметров позволяют методу быть эффективным, но работать в различных сложных ситуациях. Начальный симплекс выбирается на наше усмотрение. В данной программе точка x1 является начальной точкой, затем в программе формируются точки x2=x1+ke1, x3=x1+ke2, xn+1=x1+ken, (1.54) где k - произвольная длина шага, ej - единичный вектор. 1.9 Метод неопределенных множителей Лагранжа Естественно, что решение задач условной оптимизации значительно сложнее решения задач безусловной оптимизации [3]. Естественно стремление сведения задачи условной оптимизации (поиска относительного экстремума) к более простой задаче безусловной оптимизации (поиска абсолютного экстремума). Такая процедура осуществляется в методе Лагранжа. Рассмотрим сущность этого метода. Необходимо найти условный экстремум нелинейной функции
n переменных, при m ограничениях
Ограничения-неравенства преобразуются в равенства, а свободные члены переносятся в левые части ограничений, т.е. система (1.56) приводится к виду
В соответствии с методом Лагранжа вместо относительного экстремума функции (1.55) при ограничениях (1.57) ищется абсолютный экстремум функции Лагранжа, которая имеет следующий вид:
где Видно, что в функцию Лагранжа входит целевая функция плюс каждое ограничение, умноженное на множитель Лагранжа. Доказано, что относительный экстремум целевой функции (1.55) при ограничениях (1.57) совпадает с абсолютным экстремумом функции Лагранжа (1.58). Поиск абсолютного экстремума функции (1.58) выполняется известными методами. В частности, определяются и приравниваются к нулю частные производные функции Лагранжа:
Последние m уравнений представляют собой ограничения (1.57) оптимизационной задачи. Система (1.59) содержит (m+n) уравнений и такое же количество неизвестных. Решение системы (1.59) даст координаты абсолютного минимума функции Лагранжа (1.58) или относительного минимума целевой функции (1.55) при ограничениях (1.57). Решение системы (1.59) выполняется известными методами вычислительной математики. Если система (1.59) линейная, используется, как правило, метод Гаусса. Если система (1.59) нелинейная – метод Ньютона. 1.10 Выбор метода оптимизации Перед выбором метода оптимизации, проведем краткий анализ задач, которые должно решать разрабатываемое программное обеспечение: программа должна решать задачу условной минимизации, т.е. находить относительный экстремум, так как в математической модели кроме линейных ограничений будут иметь место и нелинейные; так как целевая функция – функция нескольких переменных, то она может иметь несколько экстремумов, и в этом случае программа должна осуществлять поиск локального минимума. Проведя анализ наиболее часто использующихся методов оптимизации, для реализации поставленной цели был выбран градиентный метод квадратичного программирования, который представляет собой наиболее эффективный из вышеперечисленных градиентных методов, модифицированный с методами полиномиальной аппроксимации. Предполагается, что целевая функция и граничные условия аппроксимируются квадратичными зависимостями или полиномами второго порядка. Более подробно этот метод будет рассмотрен далее в разделе "Разработка программного обеспечения метода оптимизации". Данный метод позволяет создать надежную программу, соответствующую всем вышеперечисленным требованиям. 2. Разработка метода оптимизации по реактивной мощности Требуемая в электроэнергетической системе (ЭЭС) суммарная мощность компенсирующих устройств определяется из уравнения баланса реактивной мощности (6.1). Эту мощность необходимо разместить в узлах электрической сети с минимальными затратами.
где
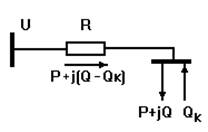
Рассмотрим простейшую схему существующей сети (рис.2.1). от источника питания с напряжением U через сопротивление сети R получает питание нагрузка мощностью S=P+jQ [9]. На шинах нагрузки установлено компенсирующее устройство мощностью Qк.
Рисунок 2.1 – Простейшая схема компенсации реактивной мощности Потери активной мощности в линии при отсутствии у
потребителя компенсирующего устройства (
При установке у потребителя компенсирующего устройства (
Таким образом, компенсация реактивной мощности позволяет уменьшить потери активной мощности в схеме электроснабжения и, следовательно, улучшить технико-экономические показатели этой схемы. Оценим влияние КУ на затраты в сети. Выражение для суммарных затрат на передачу мощности к нагрузке при установке КУ будет иметь вид:
где ЗК – затраты на КУ; соΔР – затраты на покрытие потерь активной мощности в сети; со – стоимость единицы потерянной активной мощности; зк – удельные затраты на КУ. Для определения минимума функции З приравняем к нулю ее производную от переменной QK:
Из (2.5) определяется экономически целесообразная реактивная мощность, передача которой от источника к потребителю отвечает минимуму затрат З
Величина QЭ не зависит от активной мощности Р, а зависит лишь от соотношения стоимостных показателей зк и со и параметров сети U и R, по которой передается мощность. Вопрос о размещении компенсирующих устройств в электрической сети реальной ЭЭС представляет собой сложную оптимизационную задачу. Сложность заключается в том, что электроэнергетические системы являются большими системами, состоящими из взаимосвязанных подсистем. Рассматривать изолированно каждую отдельную подсистему нельзя, поскольку свойства больших систем определяются характером взаимосвязей отдельных подсистем. При анализе больших систем используется системный подход [9,10,11], согласно которому анализ большой системы выполняется при разделении ее на подсистемы, непосредственно не связанные между собой, но влияющие друг на друга через систему более высокого уровня. Применительно к рассматриваемому вопросу электрическая сеть представляется разными уровнями, как это показано на рис. 2.2. верхний уровень – это электрическая сеть напряжением 110 кВ и выше. Эта сложнозамкнутая электрическая сеть, представляемая полной схемой замещения, показана на рис.2.2 условно, как ЭС1. Реактивные мощности, вырабатываемые генераторами электростанций QЭС, компенсирующими устройствами QК, линиями электропередачи QС, а также реактивные мощности, протекающие по связям с соседними ЭС2 и ЭС3 (Q12, Q21, Q13, Q31) обеспечивают в ЭС1 располагаемую реактивную мощность Qр1. |
|

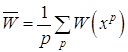
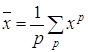 ;
;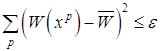
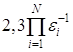 испытаний. При N=5,
i=0,01 число испытаний оценивается в 2,3 1010, что исключает возможность
непосредственного использования метода.
испытаний. При N=5,
i=0,01 число испытаний оценивается в 2,3 1010, что исключает возможность
непосредственного использования метода.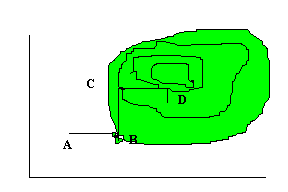
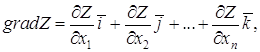 (1.14)
(1.14)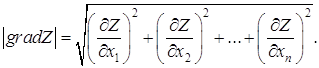 (1.15)
(1.15)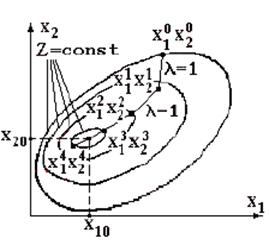
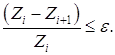 (1.16)
(1.16)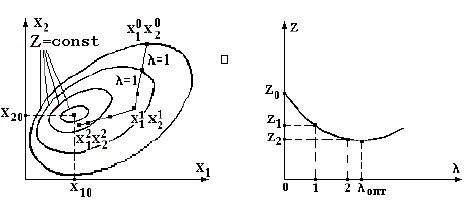
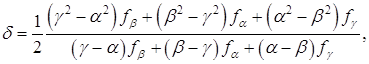 (1.22)
(1.22)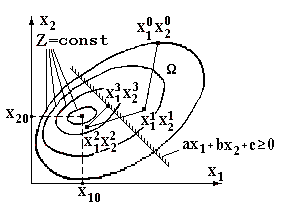
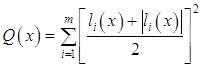 . (1.24)
. (1.24)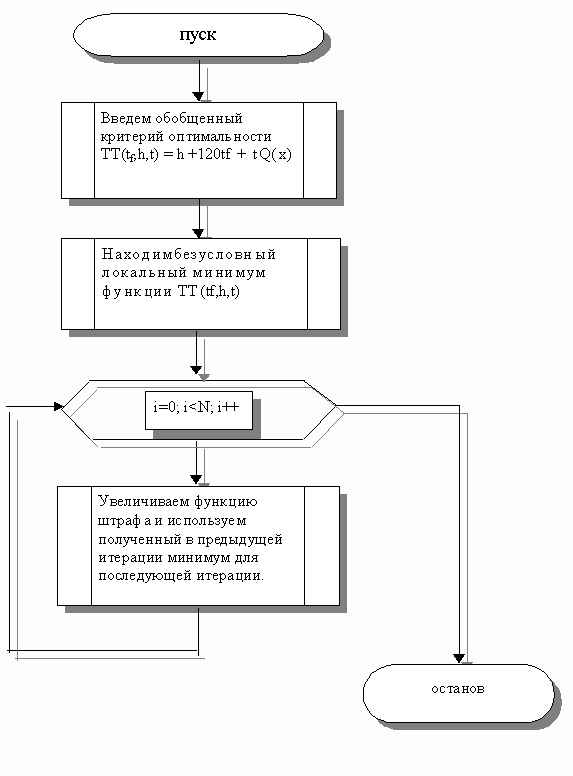
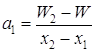
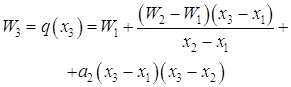
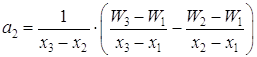
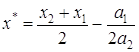
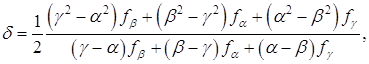 (1.29)
(1.29)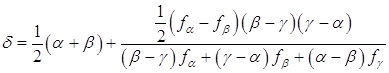 (1.31)
(1.31)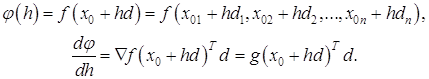 (1.32)
(1.32)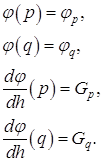 (1.33)
(1.33)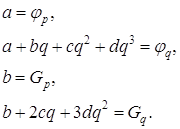 (1.34)
(1.34)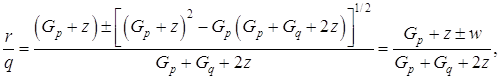 (1.35)
(1.35)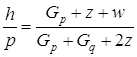
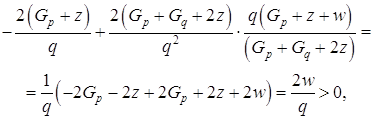 (1.36)
(1.36)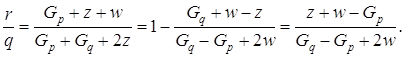 (1.37)
(1.37)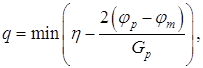 (1.38)
(1.38)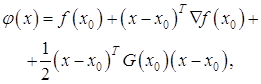 (1.41)
(1.41)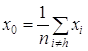 (1.47)
(1.47)

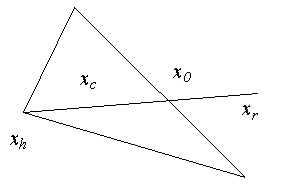

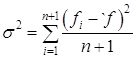 , (1.53)
, (1.53)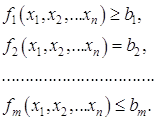 (1.56)
(1.56)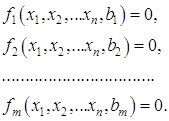 (1.57)
(1.57) (1.58)
(1.58)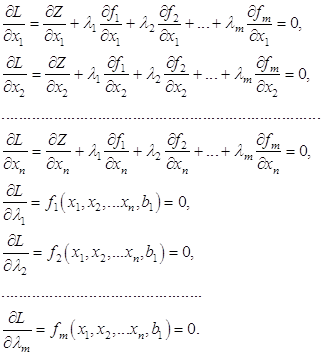
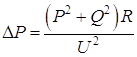 . (2.2)
. (2.2)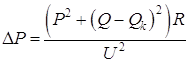 . (2.3)
. (2.3)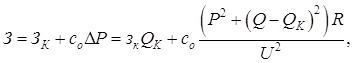 (2.4)
(2.4)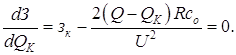 (2.5)
(2.5) (2.6)
(2.6)